みなさんこんにちは!このブログでは主に
の4つのトピックについて発信しています。
今回の記事では時系列データの分析について扱います!
本シリーズの初回記事↗で見てきたように、時系列データをそのまま相関分析や回帰分析にかけてしまうと、まったく無関係な変数同士でも強い関係があるように見える「偽相関」 が出現し、誤った結論を導く危険性があります。時系列データは多くの場合、「非定常」だからです。
では、非定常な時系列データをどう扱えばよいのでしょうか?
本記事ではその答えとして、実務でよく使われる4つの代表的な定常化手法 を紹介します。
- 差分を取る
- トレンドを除去する
- 季節性を調整する
- ARIMAモデルを活用する
👉 この記事を読めば、非定常データを定常化する基本的な方法を理解し、Pythonを使って実際に実装できるようになります。
Abstract | 非定常データを定常化する4つの方法
時系列データの分析では、データが定常であること が前提となります。
しかし実務で扱うデータの多くはトレンドや季節性を含み、そのままでは非定常です。非定常なまま分析に使うと「偽相関」や誤った回帰関係が導かれてしまうため、事前に定常化の処理を行うことが不可欠です。
本記事では、Pythonを用いて以下の4つの代表的な手法を実装し、実際にどのようにデータが定常化されるのかを検証します。
- 差分を取る(Differencing)
- トレンド除去(Detrending)
- 季節調整(Seasonal Adjustment)
- ARIMAモデルの活用
👉 この記事を読めば、非定常データを適切に処理するための基本的なアプローチが理解でき、実務で時系列データを分析するときに役立つ知識と実装スキルを身につけることができます。
Background | シリーズのこれまでと今回の位置づけ
これまでのシリーズでは、非定常データがもたらす問題と、その確認方法を順を追って解説してきました。
- 第1回:「ランダムウォークを使ったシミュレーション」で、独立したデータ同士でも 76%の確率で偽相関が出る ことを実証↗
- 第2回:「ADF検定」を用いて、データが定常か非定常かを統計的に確認できることを紹介↗
- 第3回:「トレンドや時間項を含む場合の定常性」を検証し、非定常の性質によって対応が異なる ことを確認↗
これらを踏まえて、本記事では「では、実際に非定常データをどう処理するのか?」という課題に取り組みます。
具体的には、差分、トレンド除去、季節調整、ARIMAモデル といった代表的な手法をPythonで実装し、それぞれの効果を比較します。
👉 この背景を押さえることで、本記事の目的は単なるテクニック紹介にとどまらず、実務データを扱う際の分析戦略を体系的に理解すること にあると分かります。
Method | 非定常データを処理する代表的な方法
非定常データを定常化する方法はさまざまありますが、実務でよく使われるのは以下の4つです。
- 差分を取る(Differencing)
- トレンド除去(Detrending)
- 季節調整(Seasonal Adjustment)
- ARIMAモデルの活用
ここでは、各手法の考え方と数式を整理し、どのような場面で役立つかを確認します。
差分を取る(Differencing)
時系列データには「水準が時間とともに漂ってしまう」という特徴を持つものがあります。例えば、ランダムウォーク型のデータでは、平均値が一定せず、過去の値に引きずられるように動き続けます。
このような非定常な系列に対して有効なのが「差分」です。
差分とは、ひとつ前の値との差を取って「変化量の系列」に変換する方法です。
こうすることで平均や分散が安定し、統計的な前提条件に合った形(=定常性を持つデータ)へと整えることができます(図1↗を参照)。
数式
差分には「一次差分」「二次差分」などがあります。
- 一次差分: もっとも基本的な差分で、ランダムウォーク型の非定常性を取り除くときに使います。
$$
\Delta x_t = x_t – x_{t-1}
$$ - 二次差分: 一次差分を取っても非定常性が残る場合に適用します。
$$
\Delta^2 x_t = (x_t – x_{t-1}) – (x_{t-1} – x_{t-2})
$$
一般に、一次差分 → まだ非定常 → 二次差分 → まだ非定常 → 三次差分…と、検定(ADF検定など)を繰り返しながら、必要最小限の次数で止めるのが基本です。
適用場面
差分が適しているのは、ランダムウォーク型の動きをする系列です。株価や為替レートのように、ショックの影響が長く残りやすいデータに向いています。
一方で、はっきりとした線形トレンドを持つデータの場合は、差分よりもトレンド除去(Detrending)の方が自然です。また、四半期ごとの季節性が強いデータでは、通常の差分ではなく季節差分(例:12期差分)を行う方が有効です。
メリット
- 実装が非常に簡単で、前処理としてすぐに試せる。
- 単位根型の非定常データ(ランダムウォークなど)を定常化できるケースが多い。
デメリット
- 差分の次数を上げすぎると「過差分」となり、元のデータが持っていた低周波のパターンを壊してしまう。
- 差分を繰り返すほどランダムノイズが増幅し、ばらつきが大きくなる(おおよそノイズ強度は\(\propto \sqrt{d}\)で増加。\(d\)は差分の回数)。
- 季節性が原因で非定常に見えている場合は、通常の差分では対応できない。
まとめ
👉 差分は「ランダムウォーク型の非定常性を取り除くための最初の一手」であり、
「どの程度の差分で定常化するか」を検定で確認しながら使うのが基本です。
トレンド除去(Detrending)
時系列データには「時間とともに一定方向に伸びていく」傾向(トレンド)が含まれることがあります。例えば、GDPや企業の売上高など、長期的に右肩上がりに成長するデータです。
このようなデータをそのまま相関分析や回帰にかけると、「ただ成長しているだけなのに、関連性がある」と誤解されるリスクがあります。
そのため、トレンドを回帰式などで推定して取り除き、残った部分(残差)を分析対象にするのが「トレンド除去」です(図2↗を参照)。
数式(線形トレンドの場合)
トレンドを持つ時系列\(x_t\)を次のように表します。
$$
x_t = \alpha + \beta t + \epsilon_t
$$
ここで、\(\alpha + \beta t\)がトレンド成分です。
これを推定して取り除くことで、残差\(\epsilon_t\)が「定常部分」として得られます。
適用場面
- GDPや売上高のように、経済成長や人口増加に伴って決定的に増加していくデータ。
- トレンドの形がある程度わかっていて、差分よりもトレンドをモデル化する方が自然なケース。
- トレンドが一時的なショックではなく、構造的に続いていると考えられる場合。
メリット
- トレンドの影響を除去することで、**本当に分析したい変動(残差)**に焦点を当てられる。
- 線形や多項式でモデル化できる場合は、残差の解釈がしやすい。
デメリット
- 線形や単純な多項式では複雑なトレンドには対応できない。
- トレンドの推定が誤っていると、残差も歪んでしまう。
差分との違い
- 差分:ランダムウォークのように「水準が漂う」データに強い。
- トレンド除去:決定的に「右肩上がり/下がり」するデータに強い。
どちらも「平均を安定させる」という目的は同じですが、データの性質に応じて使い分けることが大切です。
まとめ
👉 トレンド除去は「経済成長や人口増加など、構造的に続く変化」を取り除くときに有効な手法です。残差に注目することで、データの“本当の揺れ”を明らかにすることができます。
季節調整(Seasonal Adjustment)
時系列データには、毎年・毎月・毎週といった 周期的な変動(季節性) が含まれることがあります。例えば、毎年12月に売上が跳ね上がる小売業や、毎年夏に需要が増える電力使用量などです。
このような季節性を除去せずに分析すると、単に季節の繰り返しを「相関」と勘違いしてしまうことがあります。
そこで、周期成分を取り除き、基調的な動き(トレンドや残差)に注目するのが「季節調整」です(図3↗を参照)。
数式(加法モデルの場合)
季節性を含むデータは次のように分解されます。
$$
x_t = T_t + S_t + e_t
$$
- \(T_t\): トレンド(長期的な変化)
- \(S_t\): 季節成分(周期的な変動)
- \(e_t\): 残差(ランダムな揺れ)
季節調整では、このうち\(S_t\)を取り除き、\(T_t + e_t\)を分析対象とします。
適用場面
- 四半期の売上高やGDPのように、季節性が強い経済データ。
- 月次のWebアクセス数や電力消費量など、周期的な波を繰り返すデータ。
- 季節のパターンが比較的安定しているとき。
メリット
- 季節的な影響を排除し、基調的なトレンドや変動を把握できる。
- 政策判断や経営判断のように、「本質的な変化」だけを見たい場面で役立つ。
デメリット
- 季節性の周期を正しく設定できないと誤った調整になる。
- 外れ値があると季節成分の推定が歪む場合がある。
- 季節性そのものが分析対象の場合(例:消費行動の季節性分析)には不向き。
差分・トレンド除去との違い
- 差分:ランダムウォーク型の不規則な水準変動を処理。
- トレンド除去:決定的に上昇・下降する構造的な変化を処理。
- 季節調整:周期的に繰り返すパターンを処理。
それぞれ処理する「非定常性の原因」が異なるため、データの性質を見極めて選ぶ必要があります。
まとめ
👉 季節調整は「周期的に繰り返す変動」を取り除くための手法です。
基調的な変化に注目したいときには欠かせないステップとなります。
ARIMAモデルの活用
差分・トレンド除去・季節調整は「前処理」として非定常性を取り除く方法ですが、
ARIMAモデルは 「モデル内部に差分や回帰構造を組み込み、非定常な系列を直接扱える」 アプローチです。
つまり、データを無理に加工せずとも、モデル自体が「非定常を定常に変換して扱う仕組み」を持っています。
予測やシミュレーションを行う場合には、最もよく使われる手法のひとつです(図4↗を参照)。
数式(ARIMAモデル)
ARIMA(p, d, q) モデルは以下の3つの要素を組み合わせています。
- AR(自己回帰):過去の系列の影響
- I(差分):非定常を取り除くための差分
- MA(移動平均):過去の誤差の影響
差分化
まずは差分を考えます。ここで便利なのが「ラグ演算子\(L\)」です。これは「1時点前の値を参照する記号」で、
$$
L x_t = x_{t-1}, \quad L^2 x_t = x_{t-2}, \dots
$$
と定義されます。
ARIMAで使う\(d\)次差分は「繰り返し差分」であり、次のように定義されます。
$$
\Delta^d x_t = (1 – L)^d x_t
$$
例えば:
- \(d = 1\)の場合:\(\Delta x_t = x_t – x_{t-1}\)(一次差分)
- \(d = 2\)の場合:\(\Delta^2 x_t = (x_t – x_{t-1}) – (x_{t-1} – x_{t-2}) =x_t – 2x_{t-1} + x_{t-2}\)(二次差分)
と表されます。
差分化 + ARMA(p, q) = ARIMA(p, d, q)モデル
差分系列に自己回帰(AR)と移動平均(MA)の構造を持つARMA(p, q)モデルを適用したものが、ARIMA(p, d, q)モデルです。ARIMA(p, d, q) の一般形は次のように表せます。
$$
\Delta^d x_t = \phi_1 \Delta^d x_{t-1} + \cdots + \phi_p \Delta^d x_{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} + \cdots + \theta_q \epsilon_{t-q}
$$
ここで:
- \(\phi_i\):自己回帰の係数(過去の値の影響の強さ)
- \(\theta_j\):移動平均の係数(過去の誤差の影響の強さ)
- \(\epsilon_t\):平均0・分散一定のホワイトノイズ
具体例として ARIMA(1,1,1) の場合、一次差分系列\(\Delta x_t\)に対して次の式になります。
$$
\Delta x_t = \phi_1 \Delta x_{t-1} + \epsilon_t + \theta_1 \epsilon_{t-1}
$$
ここで、\(\phi_1\)は「直前の差分が現在に与える影響」、\(\theta_1\)は「直前の誤差が現在に与える影響」、\(\epsilon_t\)は「新たに発生する誤差」を表します。
係数の推定方法
実際に分析を行うときには、与えられたデータを基にして\(\phi_i\)や\(\theta_j\)を推定します。
一般的には 最尤推定法(Maximum Likelihood Estimation, MLE) が使われ、
「過去の値や誤差がどの程度現在に影響しているのか」を統計的に数値化するイメージです。
メリット
- 差分・トレンド除去・季節調整などを モデル内部に組み込める ため、事前の加工が不要になる
- 自己回帰(AR)と移動平均(MA)を組み合わせることで、複雑な依存関係を表現できる
- 将来予測まで一貫して行える(分析と予測を兼ねる)
デメリット
- モデルの次数 (p,d,q)(p, d, q)(p,d,q) を選択する必要があり、過学習や不適切なモデル選択のリスクがある
- データが十分に長くないとパラメータ推定が不安定になる
- 季節性のあるデータには SARIMA やその他の拡張モデルを使う必要がある
差分・トレンド除去・季節性除去との違い
- 差分やトレンド除去は 「前処理として非定常性を取り除く」 のが目的
- ARIMAは 「非定常性を含んだままモデル化し、内部で差分やARMA構造を組み合わせて処理する」 ところが違う
- そのため、単なる前処理よりも柔軟に対応できるが、モデルの選択と推定に注意が必要
まとめ
👉 このように、ARIMAは
- 差分を組み込み非定常を取り除き、
- 残った系列をARMA構造でモデル化し、
- 係数を推定して未来を予測する
という一連の仕組みを持った汎用的なモデルです。
Result | Pythonで各手法を試してみる
Methodセクションでは、差分化・トレンド除去・季節調整・ARIMAといった非定常データへの対処法を理論的に整理しました。
ここからはPythonを使い、実際にそれぞれの手法をデータに適用して効果を確認します。
検証の流れは以下の通りです。
- 非定常なデータを生成(ランダムウォーク+トレンドや季節性を加えた系列)
- 各手法を適用(差分、トレンド除去、季節調整、ARIMA)
- 定常化の有無を図で確認(平均・分散の安定性を視覚的にチェック)
- ADF検定を実行して統計的に判定
この流れに沿って、手法ごとに結果を見ていきましょう。
準備 | 共通関数の定義
まずはプロットとADF検定を毎回簡単に呼び出せるように、共通関数を定義しておきます。
プロット関数
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
import statsmodels.api as sm
def plot_series(original, transformed, labels, titles):
"""
Plot original and transformed time series.
"""
fig, axs = plt.subplots(2, 1, figsize=(10, 6))
axs[0].plot(original, label=labels[0])
axs[0].set_title(titles[0])
axs[0].legend()
axs[1].plot(transformed, label=labels[1], color="orange")
axs[1].set_title(titles[1])
axs[1].legend()
plt.tight_layout()
plt.show()ADF検定関数
def run_adf_test(series, label):
"""
Run ADF test and print p-value.
"""
result = adfuller(series)
print(f"ADF Test ({label}): p-value = {result[1]:.4f}")
return result[1]
差分を取る(Differencing)の実行
まずはランダムウォーク系列を生成し、一次差分を適用してみます。
差分を取ることで「系列が平均0付近に安定するかどうか」を目視し、さらにADF検定で統計的に確認します。
# Generate random walk
np.random.seed(0)
n = 200
eps = np.random.normal(0, 1, n)
x = np.cumsum(eps) # Random walk
# Apply differencing
dx = np.diff(x, n=1)
# Plot
plot_series(
original=x,
transformed=dx,
labels=["Random Walk", "First Difference"],
titles=["Non-stationary series (Random Walk)", "After Differencing (Stationary)"]
)
# Run ADF test
p1 = run_adf_test(x, "Random Walk")
p2 = run_adf_test(dx, "First Difference")時系列プロットの様子
プロットの結果は下図1のようになります。
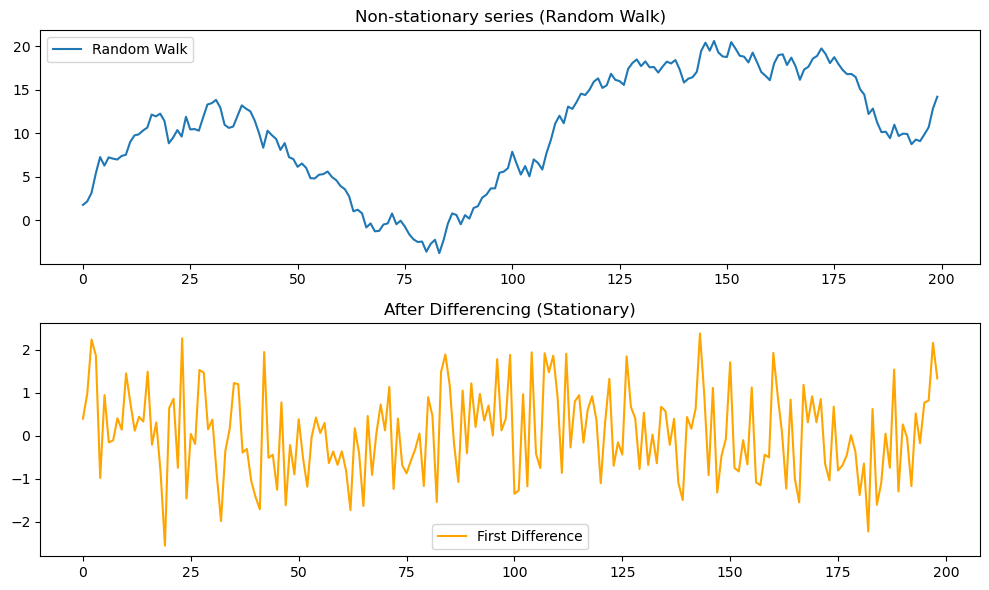
ADF検定の結果
ADF検定の結果は
ADF Test (Random Walk): p-value = 0.5869
ADF Test (First Difference): p-value = 0.0000となります。
結果の解釈
- 元のランダムウォークは平均が動き続けるため 非定常
- 一次差分を取ると、平均0付近に安定し、見た目にも定常的
- ADF検定では ランダムウォーク: p値 > 0.05(非定常), 差分後: p値 < 0.05(定常) となる
👉 差分化は最もシンプルで効果的な「定常化の第一手段」であることが確認できます。
トレンド除去(Detrending)の実行
次に、線形トレンドを含む系列を生成し、回帰を使ってトレンド成分を取り除きます。
トレンドを除去することで「残差系列が定常的に振動するか」を確認し、ADF検定で統計的に判定します。
# Generate data with linear trend
np.random.seed(0)
t = np.arange(n)
eps = np.random.normal(0, 1, n)
x_trend = 0.05 * t + eps # Linear trend + noise
# Detrending by regression
X = sm.add_constant(t) # Add constant term
model = sm.OLS(x_trend, X).fit()
residuals = model.resid # Detrended series
# Plot
plot_series(
original=x_trend,
transformed=residuals,
labels=["Series with Linear Trend", "Detrended Series"],
titles=["Non-stationary series (with Trend)", "After Detrending (Stationary)"]
)
# Run ADF test
p1 = run_adf_test(x_trend, "With Trend")
p2 = run_adf_test(residuals, "After Detrending")時系列プロットの様子
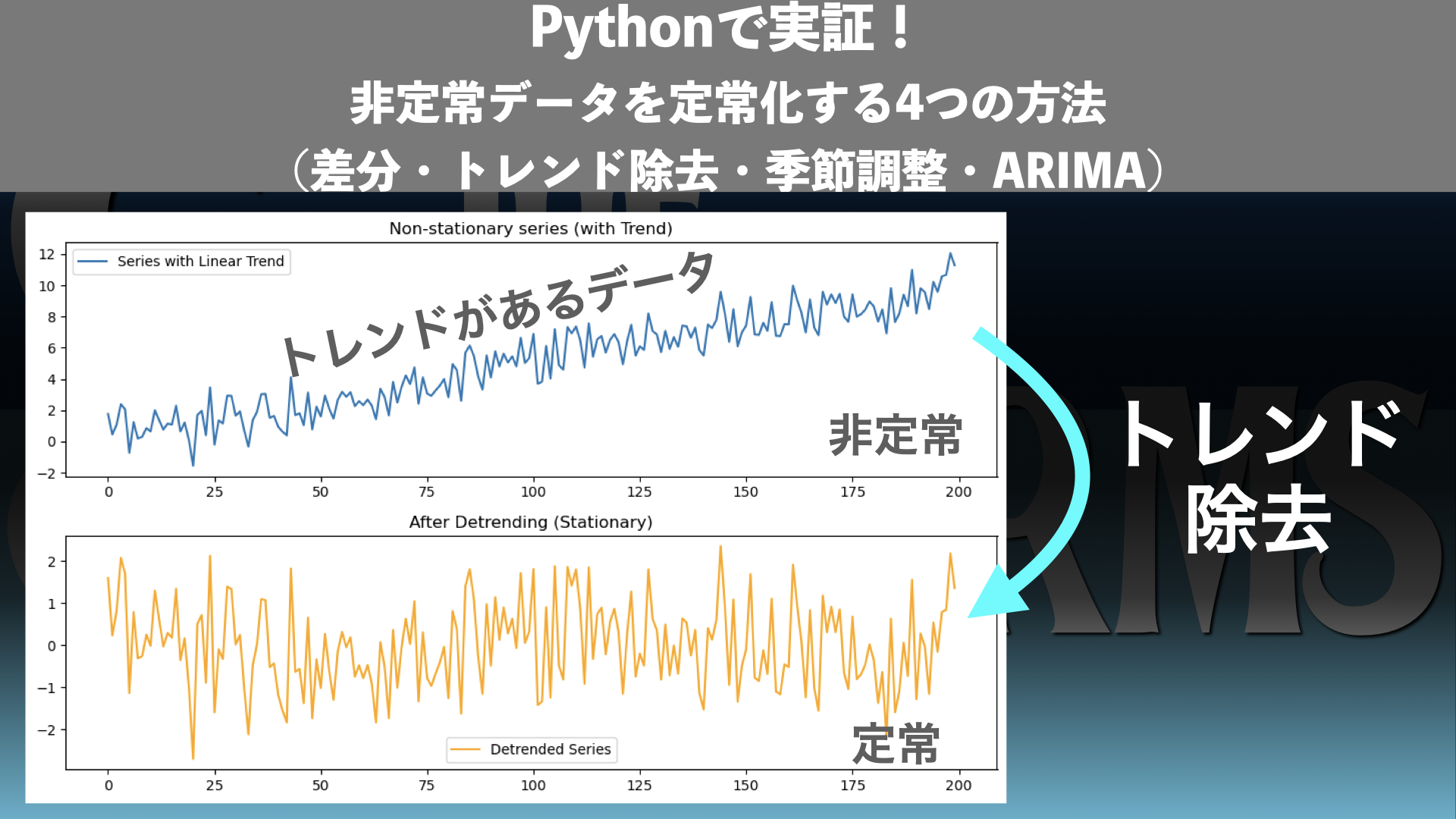
プロットの結果は下図2のようになります。
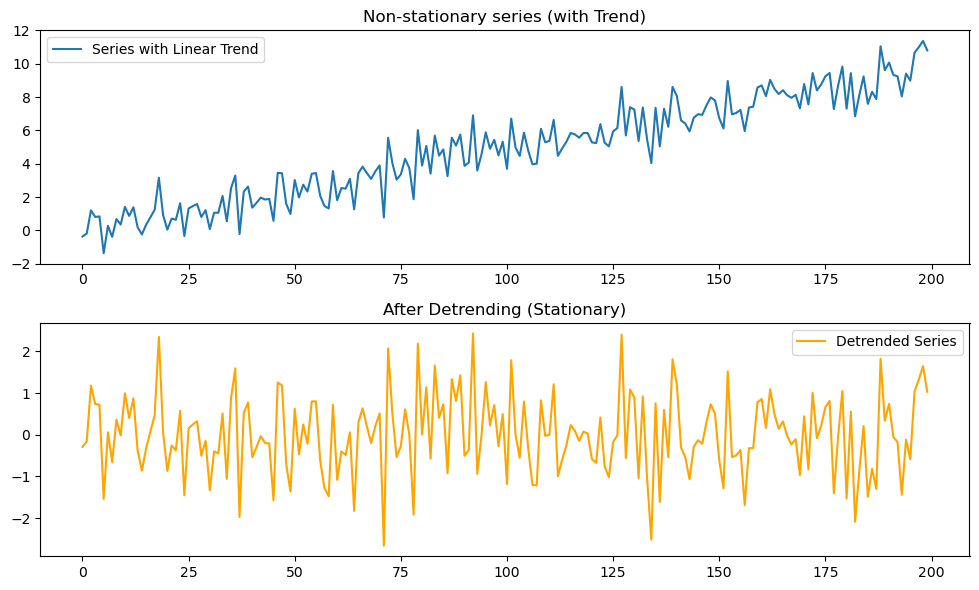
ADF検定の結果
ADF検定の結果は
ADF Test (With Trend): p-value = 0.9850
ADF Test (After Detrending): p-value = 0.0000となります。
結果の解釈
- 元の系列は時間とともに平均が上昇しており、非定常
- トレンドを回帰で取り除いた残差は、平均が安定して振動する形に変化
- ADF検定では トレンド付き系列: p値 > 0.05(非定常), 残差系列: p値 < 0.05(定常) となる
👉 トレンド除去を行うことで、「トレンド周りの定常性」を満たす系列が得られることが確認できます。
季節調整(Seasonal Adjustment)の実行
周期的な成分を含むデータを生成し、季節性を回帰で取り除きます。ここでは単純化のため、周期を既知として回帰します。
# Generate data with seasonality
np.random.seed(4)
tau = n * 0.5 # period
t = np.arange(n)
seasonal = 2 * np.sin(2 * np.pi * t / tau) # Seasonal component
eps = np.random.normal(0, 1, n)
x_seasonal = seasonal + eps
# Seasonal adjustment by regression (Fourier series with sine/cosine)
X = np.column_stack([
np.sin(2 * np.pi * t / tau),
np.cos(2 * np.pi * t / tau)
])
X = sm.add_constant(X)
model = sm.OLS(x_seasonal, X).fit()
residuals = model.resid # Seasonally adjusted series
# Plot
plot_series(
original=x_seasonal,
transformed=residuals,
labels=["Series with Seasonality", "Seasonally Adjusted Series"],
titles=["Non-stationary series (with Seasonality)", "After Seasonal Adjustment (Stationary)"]
)
# Run ADF test
p1 = run_adf_test(x_seasonal, "With Seasonality")
p2 = run_adf_test(residuals, "After Seasonal Adjustment")時系列プロットの様子
プロットの結果は下図3のようになります。
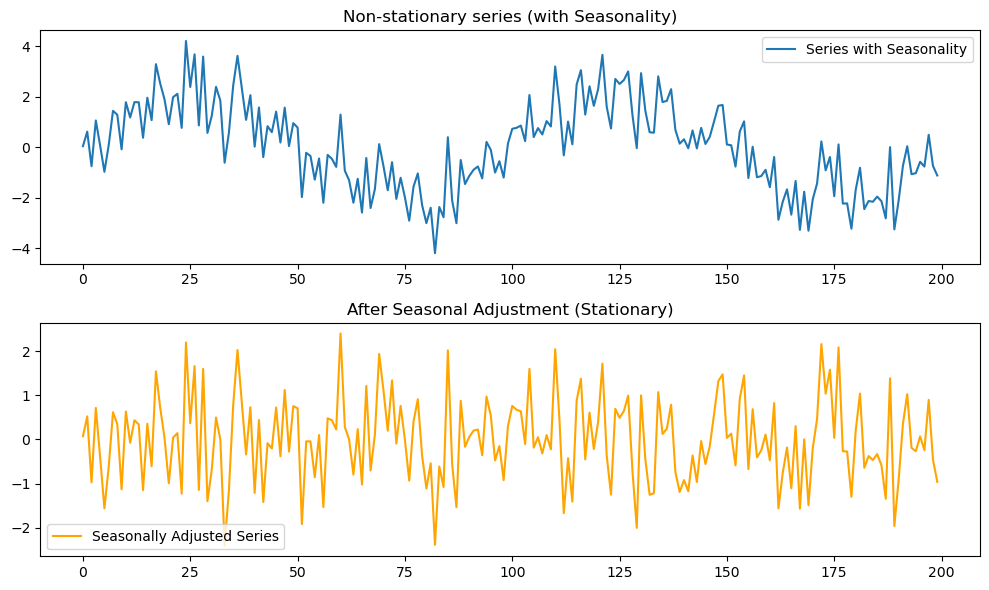
ADF検定の結果
ADF検定の結果は
ADF Test (With Seasonality): p-value = 0.3847
ADF Test (After Seasonal Adjustment): p-value = 0.0000となります。
結果の解釈
- 元の系列は周期100(サンプル数200の0.5倍に設定)のサイクルを繰り返すため、非定常。
- 三角関数を使って季節成分を取り除いた残差は、平均が安定してランダムに振動する系列になる。
- ADF検定では 季節性あり: p値 > 0.05(非定常), 季節調整後: p値 < 0.05(定常) となるケースが多い。
補足:実務での周期の扱い
今回の例では「周期 = 100」を 既知と仮定 して三角関数を使いました。
しかし、実際のデータ分析では周期が事前にわからないケースもあります。
その場合には:
- 自己相関関数(ACF) を見て周期性を推定する
- スペクトル解析(FFTなど) で支配的な周期を探す
statsmodelsのseasonal_decomposeや STL分解 を使って自動的に分解する
といった手法を組み合わせて、適切に周期を推定してから調整するのが一般的です。
ARIMAモデルの実行
ARIMAモデルは、差分やトレンド除去を前処理として行わず、モデル内部で非定常性を扱える点が特徴です。
ここではランダムウォークに近い非定常データを生成し、ARIMAモデル(次数は(1,1,1)を仮定)を当てはめて定常化を確認します。
# Generate random walk with drift
np.random.seed(4)
eps = np.random.normal(0, 1, n)
x_rw_drift = np.cumsum(eps) + 0.01 * np.arange(n) # Random walk + drift
# Fit ARIMA(1,1,1)
model = ARIMA(x_rw_drift, order=(1,1,1))
fit = model.fit()
# Get residuals
residuals = fit.resid
# Plot
plot_series(
original=x_rw_drift,
transformed=residuals,
labels=["Random Walk with Drift", "ARIMA(1,1,1) Residuals"],
titles=["Non-stationary series (Random Walk + Drift)", "After ARIMA Modeling (Residuals)"]
)
# Run ADF test
p1 = run_adf_test(x_rw_drift, "Random Walk + Drift")
p2 = run_adf_test(residuals, "ARIMA Residuals")時系列プロットの様子
プロットの結果は下図4のようになります。
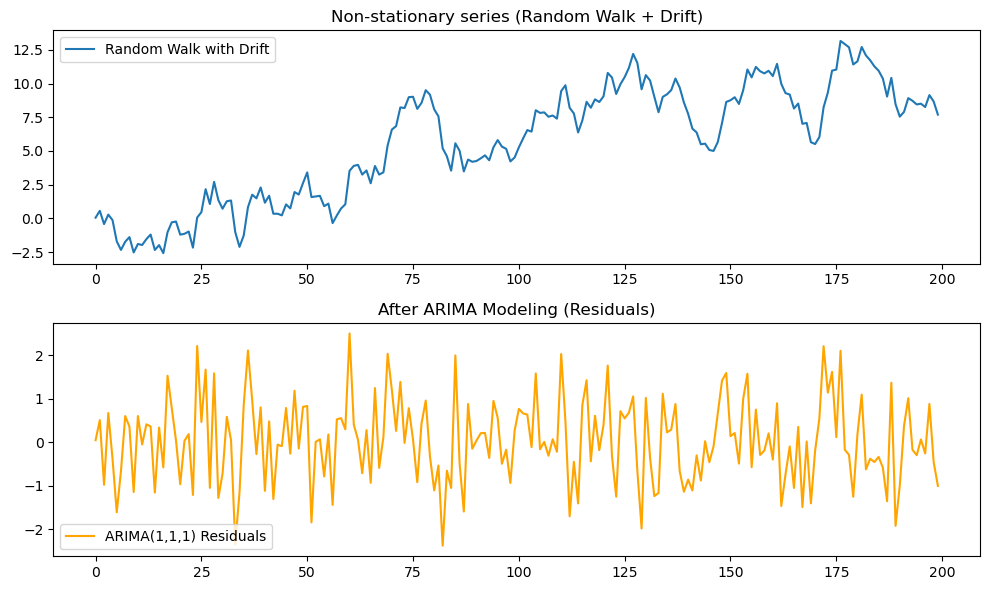
ADF検定の結果
ADF検定の結果は
ADF Test (Random Walk + Drift): p-value = 0.7142
ADF Test (ARIMA Residuals): p-value = 0.0000となります。
結果の解釈
- 元の系列はランダムウォーク+ドリフトで、平均が時間とともに変化するため 非定常。
- ARIMA(1,1,1) を適用した後の残差は、平均0のランダムな揺らぎ(ホワイトノイズ)に近くなる。
- ADF検定では 元系列: p値 > 0.05(非定常), 残差: p値 < 0.05(定常) となることが確認できる。
補足(ARIMAの次数選択について)
本記事のサンプルコードでは ARIMA(1,1,1) を例として使用しましたが、これはあくまで「よく使われる代表例」としてのデモンストレーションです。
実務においては、ARIMAモデルの次数\((p, d, q)\)は次の手順で選定するのが一般的です(詳細は割愛します)。
- 差分次数\(d)\ を ADF検定やKPSS検定で判定し、必要に応じて差分をとる。
- 自己回帰次数\(p\) は偏自己相関関数(PACF)の形から推定。
- 移動平均次数\(q\) は自己相関関数(ACF)の形から推定。
- 複数の候補モデルを当てはめ、AICやBIC を基準に比較して最適なモデルを選択。
したがって、ここで示す ARIMA(1,1,1) のコードは「一例」であり、実データにそのまま適用できるとは限りません。実務では必ずデータの性質に応じてモデル選定を行ってください。
Discussion | 実務への示唆
本記事で紹介した 差分・トレンド除去・季節調整・ARIMA は、非定常データを定常化するための代表的なアプローチです。
しかし、実務で扱うデータは千差万別であり、どの手法を適用するかは「データの性質」と「分析の目的」によって大きく変わります。
ここでは、実務におけるポイントと注意点を整理し、さらにARIMAから発展できるモデル群について触れます。
データの性質に応じた前処理の重要性
非定常データとひとことで言っても、その原因は多様です。
- ランダムウォークのように、系列が累積的に変動してしまう場合
- 経済指標や人口データのように、長期的なトレンドを持つ場合
- 売上や気温のように、明確な季節性を伴う場合
まずは「なぜ非定常なのか」を見極めることが最初のステップです。
原因を把握していないまま処理を行うと、過剰な調整や誤った前処理につながり、分析結果に大きな歪みを生じさせます。
手法選択の指針
データの性質に応じて、以下のような使い分けが考えられます。
- 差分(Differencing)
単純なランダムウォーク的な非定常に対して有効。 - トレンド除去(Detrending)
線形・非線形のトレンドが支配的な系列に適用。残差に注目することで「変動部分」を分析できる。 - 季節調整(Seasonal Adjustment)
周期性が既知で明確な場合に有効。売上、アクセス数、経済統計などでよく利用される。 - ARIMA
差分+自己回帰+移動平均を組み合わせ、幅広い系列に対応できる柔軟な手法。
特に予測を目的とする場合に強力。
👉 ポイントは、「どの方法が必ず優れている」というわけではなく、分析の目的とデータの特徴に応じて最適な手法を選ぶこと です。
実務での落とし穴と注意点
実務で非定常データと定常化する際の代表的な注意点をまとめます。
- 過剰な差分化
差分を繰り返すと系列がホワイトノイズ化し、情報が失われる。必要最小限にとどめることが重要。 - 季節性周期の誤認
季節性の周期を誤って設定すると、トレンドやノイズを誤って取り除いてしまうリスクがある。周期はACFやスペクトル分析で慎重に確認する。 - ARIMAの次数選択
ARIMAは柔軟だが、(p,d,q) の選び方を誤ると過学習や不安定なモデルにつながる。ACF/PACFやAIC/BICで検証するのが基本。
ARIMAから広がる発展モデル
ARIMAは定常化とモデリングを一体化できる強力な枠組みですが、さらに発展的なモデルへと拡張できます。
- SARIMA: 季節性を直接組み込むモデル。
- VAR(Vector AutoRegression): 複数の系列を同時に扱い、相互依存関係をモデル化。
- 状態空間モデル: より柔軟にトレンド・季節性・外生要因を取り込む枠組み。
つまり、ARIMAは「ゴール」ではなく、実務でさらに高度なモデルへ展開するための 出発点 となります。
まとめ
👉 まとめると:
- 非定常データの「原因」を理解することが最初の一歩。
- 差分・トレンド除去・季節調整・ARIMAを適切に使い分けることが重要。
- 前処理は必要最小限にとどめ、誤った処理や過剰処理を避けること。
- ARIMAは基本でありつつ、より発展的なモデルへの橋渡しにもなる。
Conclusion | まとめ
最後までお読みいただきありがとうございました!
本記事では、非定常データを定常化するための代表的な4つの方法を取り上げ、理論とPython実装を通して確認しました。
- 差分(Differencing):シンプルかつ強力だが、過剰な差分化に注意。
- トレンド除去(Detrending):長期的な傾向を取り除き、変動部分を分析。
- 季節調整(Seasonal Adjustment):周期的パターンを分解して残差に注目。
- ARIMAモデル:差分+自己回帰+移動平均を組み合わせた包括的手法。
👉 まとめると:
- 非定常データの「原因」を理解することが最初の一歩。
- 差分・トレンド除去・季節調整・ARIMAを適切に使い分けることが重要。
- 前処理は必要最小限にとどめ、誤った処理や過剰処理を避けること。
- ARIMAは基本でありつつ、より発展的なモデルへの橋渡しにもなる。
次回は、ここで学んだ手法を 実データのケーススタディ に適用し、どのようにモデル構築につなげられるかを解説していきます。
References | Pythonコードの全文
今回の記事で書いたPythonコード(Jupyter Notebook)の全文は以下です。ご参考にどうぞ!
時系列分析シリーズ
- 偽物の相関(76%)を実証!ランダムウォークに潜む落とし穴
- ADF検定で定常性を確認すべし
- トレンドや時間項を含む場合の定常性
- (今回)非定常データの対処法(差分・トレンド除去・季節調整・ARIMA)
- (次回)実データのケーススタディ

コメント