Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信していきます。
今回は久しぶりの統計学&pythonレシピです!
pythonレシピは政府統計のデータを分析する記事、統計学レシピはJohnsonのSU分布の記事以来となりました。
本シリーズでは、任意の確率分布から任意の個数のランダムサンプルを得る方法をご紹介します!
初回の今回は、「そもそも任意の確率分布からランダムサンプリングしたい場合」がどのようなときか、というところから始めます!
本シリーズ2回目(次回)以降では、任意の確率分布からランダムサンプルを得る方法を紹介していきます。
現実のデータを扱っていると、一様分布や正規分布といった一般的な確率分布ではなく、もっと複雑な関数形の確率分布や規格化されていない分布からサンプルを得たい場合があります。
今回は、「そもそもどのようなときに任意の確率分布からのランダムサンプルが必要となるのか」その問題設定としての例をご紹介します!
楕円軌道上の人工衛星の位置(位相角)の分布というかなりマニアックな例ですが、ぜひ最後までお付き合いください!
- Abstract | 実世界のデータは一般的な確率分布に従わない場合がある
- Background | 日常生活でお世話になっているランダムサンプリング
- Contents1 | 任意の分布からサンプリングする例
- Contents2 | 任意の確率分布からのサンプリング — 人工衛星はどこに見える?
- Conclusion | まとめ
Abstract | 実世界のデータは一般的な確率分布に従わない場合がある
実世界のデータは、一様分布や正規分布といった一般的な確率分布に従わない場合があります。
以前の記事では、正規分布に歪度と尖度を導入した拡張版として、Johnson SU分布をご紹介しました。
Johnson SU分布も含め、確率分布としてよく用いられる関数については、その分布関数からランダムサンプリングを得るためのライブラリが用意されています(pythonではnumpy.randomやscipy.statsなど)。
ところが、実世界のデータは、
- 確率分布の関数形が複雑
- 規格化定数が求まらない(確率分布関数の積分が1になっていない)
といった理由で、一般的な確率分布関数からサンプルを得る手法が使えない場合があります。
今回の記事では、確率分布からランダムサンプルを得たい場面として、ベイズ推定を簡単にご紹介します。
その上で、任意の確率分布からランダムサンプルを得る必要性が生じる例を取り上げます。
かなりマニアックではありますが、地球を周回する人工衛星の位置の分布です!
地球を周回する人工衛星の位置の確率分布は
$$
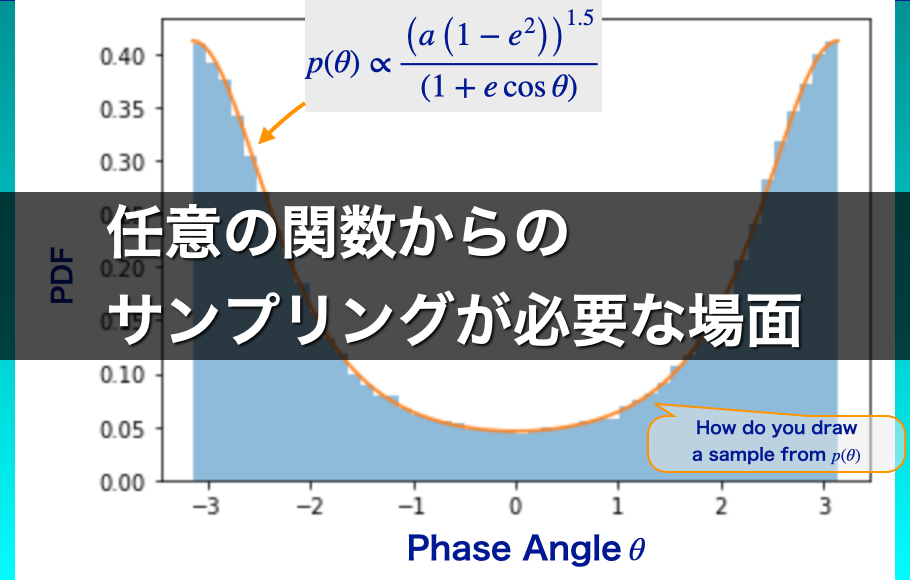
p(\theta) \propto \frac{\left(a \left(1 – e^{2}\right)\right)^{1.5}}{\left(1 + e \cos \theta \right)}
$$
という、複雑かつ規格化定数がわからない形で書かれます。
このときに、人工衛星の位置のランダムサンプルを得るには「任意の確率分布からランダムサンプル方法」を使う必要があります。
Background | 日常生活でお世話になっているランダムサンプリング
確率分布からのランダムサンプリングは、実は日常生活でも頻繁に使われています。
例えば、
- サイコロを振る
- ルーレットを回す
- コイントスをする
- 六角形の鉛筆を転がす
- サンダルを放り投げて裏表を出す
といったことは、「離散確率分布からのランダムサンプリング」にあたります。
例えば人生ゲームでは、1から10までの数値が振られたルーレットを回し、出た目の数だけ先に進みますよね。
通常、ルーレットの目が出る確率はどの数値でも同じなので、1から10までの離散一様分布からランダムサンプリングを行っていることになります。
他の例として、選択式テストの回答を決めるのに、六角形の鉛筆を転がすような場合もランダムサンプリングですね笑
他にも、コイントス、くじ引きなど、挙げればキリがないですが、みんなランダムサンプリングを経験したことがあるのです。
Contents1 | 任意の分布からサンプリングする例
データサイエンスやデータ解析の世界でもランダムサンプリングは様々な形で使われます。
どのようなときに確率分布からのランダムサンプリングが必要となるのか、お話します。
(一般的な)確率分布からのサンプリング | ベイズ推定
データサイエンスの文脈において、確率分布からのサンプリングを行う最たる例としては、ベイズ推定(Bayesian inference)があります。
こではごく簡単にベイズ推定について説明します。
ベイズ推定では、未知のパラメータを推定する際に、そのパラメータの確率分布を推定します。
ベイズ推定ではまず、パラメータの事前分布(観測や測定を行う前にわかっている情報から想定した分布)を設定しておき、観測や測定が得られたときに、その観測や測定が最も尤もらしく再現されるような分布(事後分布)に更新していくということを行います。
このような過程のなかで確率分布からのサンプリングを行います。
ベイズ推定の例 | そのパスタは一袋何g?
ベイズ推定の例を一つ紹介しましょう。
1袋500gと袋に書かれているパスタを7つ購入しました。
袋を開けて、実際に重量を測定してみると、以下のような結果が得られました。
504.3, 507.4, 498.6, 507.6, 509.7, 504.1, 502.5
このような結果が得られたときに、1袋500gという表示はどの程度信頼できるでしょうか?
統計学では、母集団(population)と標本(sample)という言葉で表されます。
上記の7つは標本であり、「1袋500g」という表記は、1袋の真の重量(=母平均)が500gであるということに相当します。
ベイズ推定を使うと、「この測定結果(標本)が得られたときに、1袋の真の重量(母平均)が500g以下である条件付き確率」を得ることができます。
このような「測定が得られた条件のもとでの条件付き確率」のことを事後分布といいます。
この例題については、別の記事で詳しく取り上げたいと思いますのでお楽しみに!
ベイズ推定の肝 | わからないことはわからないまま扱う
確率分布からのサンプリングが役立つのは、「わからないことをわからないまま扱いたい」ときです。
ベイズ推定においても肝となるのは、「わからないことをわからないまま扱う」ところです。
ベイズでは、求めたいパラメータの事前分布を仮定します。
これは測定が得られる前に想定される分布であって、通常はほとんど情報がありません。
例えば、上の例では、1袋の真の重量は500gに近いことはわかっていますが、正確にどの値かはわかりません。
したがって、1袋の真の重量の事前分布を仮定するときに、わかっていることとわかっていないことを折り込みます。
- わかっていること: 1袋の真の重量は500gぐらい
- わかっていないこと: 1袋の真の正確な重量
なので、事前分布として、それなりの幅を持っており、中心が500gの分布、例えば正規分布などを仮定することになります。
以下では、天文学の例をもう少し掘り下げます。
Contents2 | 任意の確率分布からのサンプリング — 人工衛星はどこに見える?
天文学(といっても私の専門の銀河天文学とはかけ離れた話題)で、任意の確率分布からのサンプリングが必要となる例を紹介します。
前提となる問題設定 | A地点から\(\delta_{A}\)の位置に観測された人工衛星。B地点からは観測したときに見える位置(\(\delta_{B}\))は?
地球上のあるA位置、例えば東京から人工衛星を観測したとしましょう。
この人工衛星が別の場所、例えば赤道上のB地点(簡単のために東経は東京と同じにします)から観測したとき、天球上のどこに見えるかということを考えます(図1)。
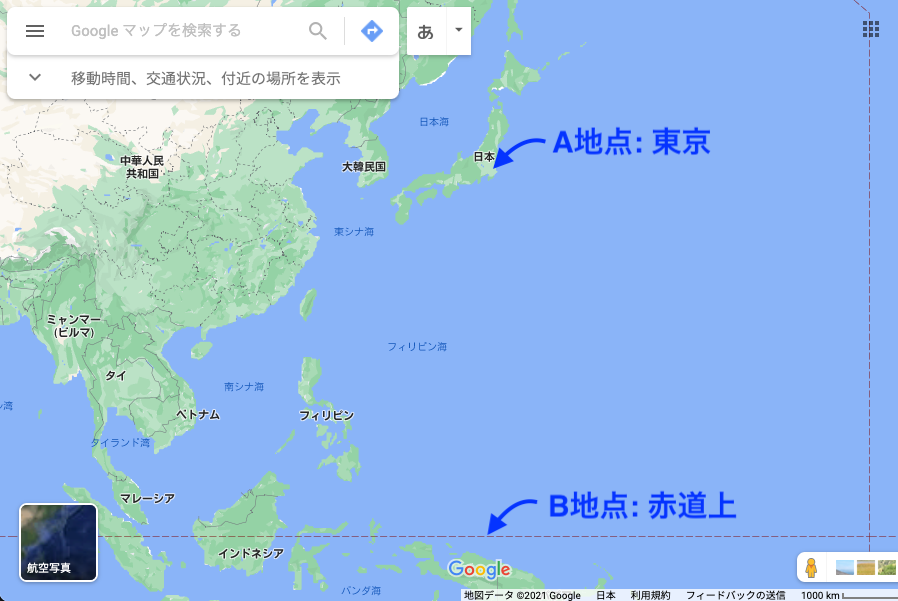
ちなみに、夜空が暗いところに行けば、人工衛星は肉眼でも観測することができます。
日没直後や日の出直前に夜空をじーっと見上げていると、キラキラした点がゆっくりと動いているのが見えます。
陽の光を反射した人工衛星です。ぜひ眺めてみてください。
話を問題設定に戻します。
A地点においてある時刻に、天球上で\(\delta_{A}\)という位置に人工衛星が見えているとします。
ちなみに、天文学では天球上の位置は、2000年の春分点からの東西方向の角度(赤経: Right Ascension; RA; \(\alpha\))と、赤道からの南北方向の角度(赤緯: Declination; Dec; \(\delta\))で表現します。
ここでは、簡単のためにDecだけを考えます。
A地点から見た人工衛星のDecが\(\delta_{A}\)ということです。
同時刻に、B地点から同じ人工衛星を見た位置(Dec)を\(\delta_{B}\)とします。
問題設定としては、A地点からDec = \(\delta_{A}\)で見えている人工衛星が、B地点からみたらどのDecに見えるかということです。
図2のように、これは人工衛星までの距離によって異なります。
つまり、人工衛星までの距離がわからないと、\(\delta_{A}\)から\(\delta_{B}\)を求めることができないということになります。
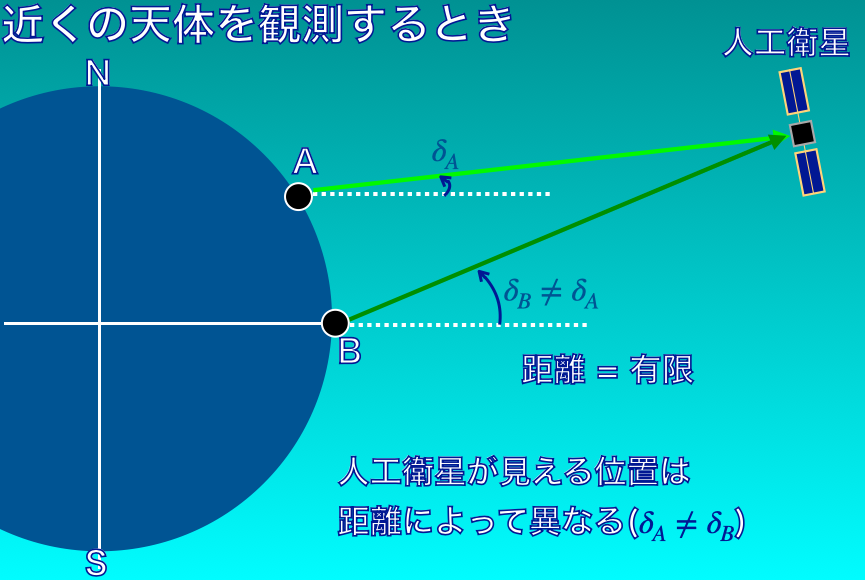
問題解決に必要だけれども不明なパラメータ | 距離がわかならい
ここで問題になるのが、天体の観測からは距離がわからないということです。
距離がわからなければ、A地点からDec = \(\delta_{A}\)に見えている人工衛星がB地点からどのDecに見えるのか、すなわち\(\delta_{B}\)を計算することはできません。
閑話休題 | 銀河天文学では距離がわからなくても\(\delta_{B}\)が求まる
実は銀河天文学では上記の問題は生じません。
なぜなら、銀河はとっても遠くにあるため、A地点から銀河までの距離とB地点から銀河までの距離の差は無視できます。
そのため、A地点からの銀河への視線とB地点から銀河への視線は平行とみなすことができます。
したがって、\(\delta_{A} = \delta_{B}\)が成り立つのです(図3)。

ちなみに、我々の住んでいる天の川銀河のお隣のアンドロメダ銀河(M31)までの距離は0.8 Mpc(メガパーセク) = 約250万光年です。
A地点とB地点の距離はせいぜい地球1週 = 1/7 光秒のオーダーです。
250万光年と比べるとほぼゼロですから、地球上のどの地点からアンドロメダ銀河を見ても同じ場所に見えると考えて良いわけです。
ベイズ的位置推定 | 距離の分布を仮定して\(\delta_{B}\)の分布を求める
人工衛星までの距離がわからないと、B地点から観測したときの位置\(\delta_{B}\)を計算することができません。
しかし、だからといって、人工衛星がB地点からどこに見えるのか、全く検討がつかないわけではありません。
A地点から人工衛星までの距離は、ゼロから無限大のどこかのはずです。
相手が人工衛星であるならば、地球のまわりを回っている(重力に束縛されている)はずなので、そんなに遠くにはないはずです。
ちなみに、A地点から人工衛星までの距離が取りうる最大値は以下のように考えることができます。
地球の重力圏と太陽の重力圏の境目であるHill半径は地球から太陽に向かって約150万kmのところにあります。
もし人工衛星がこれよりも遠くに離れてしまうと、地球を周回することはできなくなり、太陽を周回する軌道をとることになります。
なので、地球を周回する人工衛星であれば、A地点から人工衛星までの距離は、ゼロから150万kmのどこかであると考えられます。
このような情報があれば、B地点から観測したときの位置\(\delta_{B}\)をある程度の範囲に絞り込むことができます。
この考え方を一歩進め、A地点から人工衛星までの距離の確率分布を仮定します(図4)。
このように人工衛星までの距離の確率分布を仮定すると、B地点から観測したときの位置\(\delta_{B}\)も確率分布として表現することができます。
求められた(\delta_{B}\)の分布は、(\delta_{A}\)という観測が与えられたときの事後分布と考えることができます。
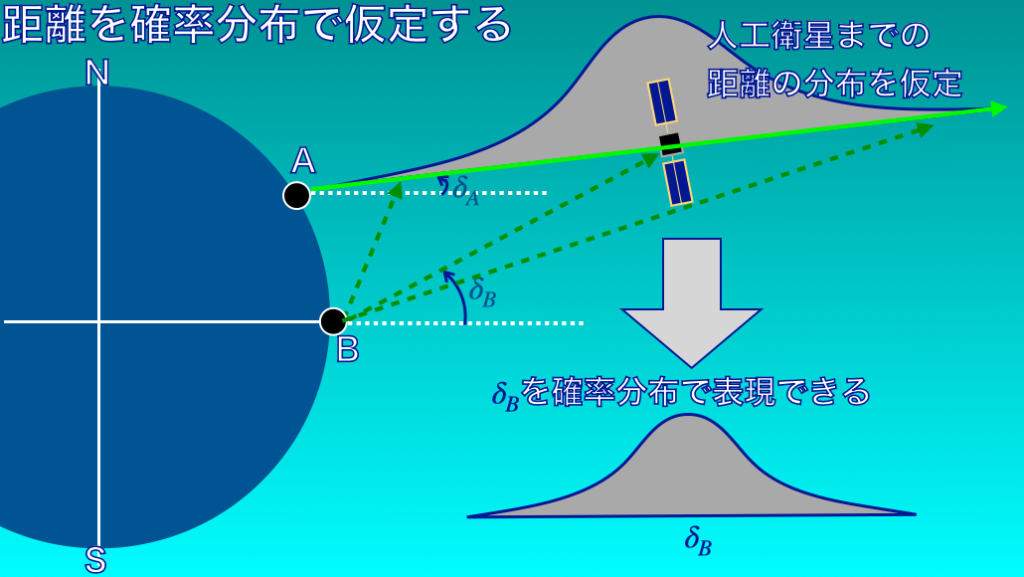
(\delta_{B}\)の確率分布が推定できて嬉しいことの例を一つ上げます。
例えば、A地点から観測された人工衛星(距離不明)をB地点からも観測したいときに、空のどの範囲を観測すればよいか、(\delta_{B}\)の確率分布から考えることができます。
(\delta_{B}\)が取りうる確率の高い領域を重点的に観測すれば、B地点から同じ人工衛星を観測できそうです。
もし実際に観測できれば、三角測量で距離を求めることができますね。
人工衛星までの距離の確率分布は?
では、人工衛星までの距離の確率分布はどのように仮定すれば良いでしょうか?
統計学の教科書などでは、正規分布や一様分布といった一般的な分布が仮定されることが多いです。
しかし、ここではもう少ししっかりと物理的な背景を考えたいとします。
人工衛星までの距離は離心率\(e\), 半長軸\(a\), 位相角\(\theta\)で決まる
人工衛星までの距離は、人工衛星の軌道の形と人工衛星が今いる位置に依存します。
人工衛星の軌道は(摂動などの細かいことはさておき)、地球を焦点とする楕円軌道を描きます。
そして、人工衛星までの距離は、
- 楕円の離心率(\((0 \geq e < 1)\); 真円からどれだけ歪んでいるか)
- 半長軸の長さ(\(a\); 楕円の大きさ)
- 観測した時の人工衛星の位相角(\(\theta\); 楕円のどこにいるか)
で決まります(図5)。
したがって、人工衛星までの距離の分布は、これら3つのパラメータを反映させる必要があります。
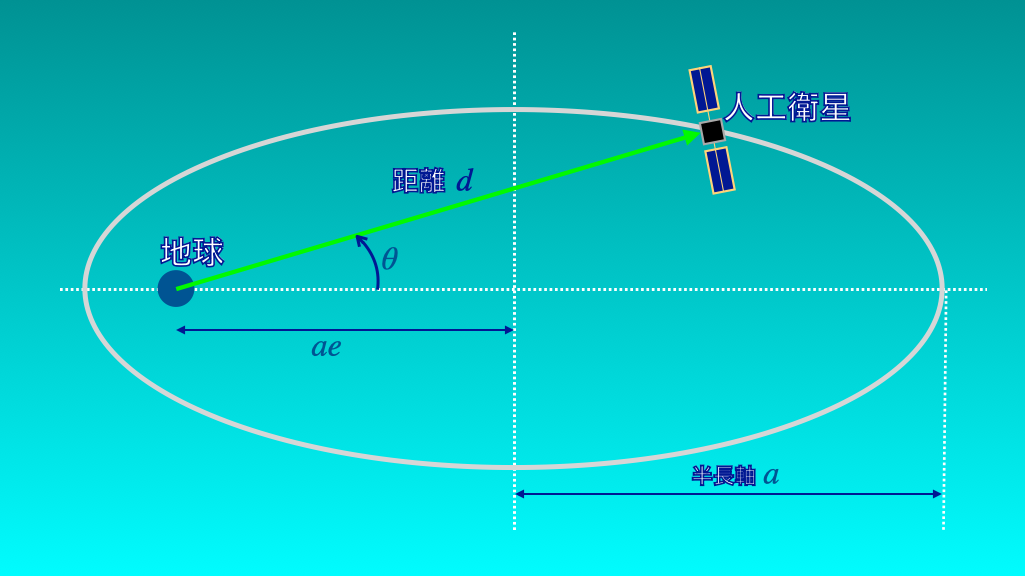
さて、いま人工衛星の素性はまったくわかっていないことにしましょう。
したがって、\(e, a, \theta\)は未知です。
未知のパラメータは確率分布を仮定して考えます。
\(e, a, \theta\)それぞれの確率分布から、ランダムサンプルが抽出できれば、人工衛星までの距離のランダムサンプルを得ることができます。
したがって、人工衛星までの距離のランダムサンプルを得る命題は、\(e, a, \theta\)のランダムサンプルを得る問題に置き換わりました。
離心率\(e\)の確率分布 | 一様分布
まず、離心率\(e\)は情報がないので\(0 \geq e < 1\)の一様分布とします。
つまり、離心率\(e\)の確率分布\(p(e)\)は
$$
p(e) = \mathrm{Uniform}(0,1)
$$
です。
半長軸(近地点距離)の確率分布 | 一様分布
半長軸は地球から近地点(地球に近い側の楕円の端っこ。図5の左端)までの距離で決めましょう。
地球から近地点までの距離、近地点距離は\(d_{P} = a(1-e)\)と表されます。
地球周回の人工衛星なので、近地点距離は、せいぜい高度100 km(地球中心からは6500 kmぐらい)から月の軌道(38万 km)ぐらいまでに入るでしょう。
なので、\( 6500\ \mathrm{km} < d_{P} < 380000\ \mathrm{km} \)の一様分布としましょう。
したがって、近地点距離の確率分布\(p(d_{P})\)は
$$
p(d_{P}) = \mathrm{Uniform}(6.5 \times 10^{6}\ \mathrm{m}, 3.8 \times 10^{8}\ \mathrm{m})
$$
です。
位相角(楕円軌道上の位置)の確率分布 | かなり複雑な分布
位相角\(\theta\)はどうでしょうか?
人工衛星がどの位相角で観測される可能性が高いかを考えたとき、速度が遅いところの方が観測されやすいでしょう。
したがって、\(\theta\)が従う確率分布\(p(\theta)\)は、その時間微分\(\dot{\theta}\)に反比例するはずです。
つまり、
$$
p(\theta) \propto \frac{1}{\dot{\theta}}
$$
となります。
位相角の分布はすでにかなり複雑になりそうな予感がしますね。
しかも、規格化することはできなさそうです(\(\propto\)は比例するという意味の記号)。
\(\dot{\theta}\)は、\(\theta\)に以下のように依存します。
$$
\dot{\theta} \propto \frac{\left(1 + e \cos \theta \right)}{\left(a \left(1 – e^{2}\right)\right)^{1.5}}
$$
したがって、\(\theta\)が従う確率分布\(p(\theta)\)は
$$
p(\theta) \propto \frac{\left(a \left(1 – e^{2}\right)\right)^{1.5}}{\left(1 + e \cos \theta \right)}
$$
となります。
ちなみに、半長軸\(a\)を近地点距離\(d_{P} = a (1-e)\)で置き換えると
$$
\dot{\theta} \propto \frac{\left(1 + e \cos \theta \right)}{\left(d_{P} \left(1 + e\right)\right)^{1.5}}
$$
$$
p(\theta) \propto \frac{\left(d_{P} \left(1 + e\right)\right)^{1.5}}{\left(1 + e \cos \theta \right)}
$$
となります。
ここで位相角\(\theta\)の確率分布\(p(\theta)\)は、一様分布や正規分布といった一般的な確率分布ではありません。
グラフにすると図6のようになります。
\(\theta\)のランダムサンプルを得るには、この複雑な確率分布からサンプルを抽出する必要があります。
これには、「任意の確率分布からサンプルする方法」を用いる必要があるのです。

任意の確率分布からサンプルできることの重要性
これまで見てきた例のように、未知のパラメータが何らかの確率分布に従っていると仮定して分析を進めることが有用な場合が多々存在します。
その場合には、その確率分布からそのパラメータをサンプルして分析を進める(上の例であれば\(\delta_{B}\)を計算する)必要があります。
では、確率分布から未知のパラメータをサンプルするにはどのようにすればよいでしょうか?
確率分布が一様分布や正規分布のような一般的な分布の場合には、たいていはランダムサンプルを得るためのライブラリが用意されています(numpy.random, scipy.statsなど)。
しかし、一様分布や正規分布のような一般的な分布でない確率分布を仮定したい場合には、別の方法をと必要があります。
任意の確率分布からサンプルを得る方法としては、
- 変数変換を用いた解析的な手法
- 確率的なサンプリングを用いた手法
の2通りがあります。
累積分布関数の逆関数が求まる場合には、1の解析的な手法(逆関数法)を取ることができます。
しかし、確率分布関数の関数形が複雑であるなど、累積分布関数の逆関数が求まらない場合も多々あります。
また、確率分布関数の関数の形はわかるものの、規格化されていない(確率分布関数の積分が1にならない)場合や規格化定数が計算できないといったことが、実際のデータを扱う際には頻繁に起こります。
そのような場合には、2の確率的なサンプリング手法を用いる必要があります。
本シリーズでは次回以降、確率的なサンプリング手法を具体的に紹介します!
特にnumpyを用いた高速なpython実装方法もご紹介しますので、お楽しみに!
Conclusion | まとめ
最後までご覧いただきありがとうございました!
任意の確率分布からのサンプリングが必要になるケースをご紹介しました!
ベイズ推定など、わからないパラメータをわからないまま分析を進めるといった場合に、確率分布からのサンプリングが必要です。
データ分析の教科書では、正規分布や一様分布といった一般的な確率分布を仮定するケースが多いですが、実際にデータ解析をしているとそのような一般的な分布ではなく、任意の確率分布関数(しかも規格化できていない)からサンプリングしたい場面が出てきます。
今回は、任意の確率分布関数からのランダムサンプリングが必要となる場面として、人工衛星の楕円軌道上の位置(位相角)の例をご紹介しました!
実世界のデータは、一様分布や正規分布などの一般的な確率分布では表現できない分布に従うことがあります。
そにょうな場合には、任意の確率分布関数からサンプリングを行う必要があります。
次回以降では、任意の確率分布関数からサンプリングを行う方法をご紹介します!
以上、「統計学&pythonレシピ | 任意の確率分布からのサンプリング1(問題設定編)」でした!
またお会いしましょう!Ciao!
コメント