Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信していきます。
今回は統計学&pythonレシピです!
本シリーズでは、任意の確率分布から任意の個数のランダムサンプルを得る方法をご紹介しています!
シリーズ第2回と第3回では、そのための2つの手法
- 棄却サンプリング (rejection sampling)
- MHサンプリング (Metropolis-Hastings sampling)
の概要をご紹介します!
ちなみにシリーズ第1回では、任意の確率分布からのサンプリングが必要になる例をご紹介しました。
今回は、棄却サンプリングをご紹介します。
棄却サンプリングはマルコフ連鎖を使わない単純かつ直感的なサンプリング方法です。
棄却サンプリングの手順と仕組みに加え、pythonによる簡単な実装例をご紹介します。
今回は棄却サンプリングの仕組みが理解しやすいよう簡単な実装方法をご紹介しますが、第4回ではnumpyライブラリを用いて高速実装する方法をご紹介しますので、そちらもお楽しみに!
複雑な関数形の確率分布からサンプルを得ようとすると、既存のライブラリや逆関数法が使えないことがあります。
通常、確率分布からのサンプリング問題と聞くと、一様分布や正規分布などの一般的な確率分布からのサンプリングを思い浮かべる方が多いと思います。
このような一般的な確率分布からのサンプリングについては、さまざまな計算ライブラリ(numpy.random, scipy.statsなど)で実装可能です。
また、累積分布関数の逆関数が求められる場合には逆関数法と呼ばれる解析的な計算が適用できます。しかし、一般的な確率分布ではなかったり、確率分布の関数形が複雑だと、既存のライブラリや逆関数法は使えません。
このようなときに、棄却サンプリングやMHサンプリングといった非解析的な手法が役に立ちます。
これらの方法であれば、何かしらの方法で確率分布が定式化できれば、その確率分布からランダムサンプルを得ることができます。
しかも、確率分布の規格化が不要(積分が1になる必要がない)なため、大変便利です!
今回は、「任意の確率分布(しかも規格化できていない)からランダムサンプルを得るにはどうしたらいいんだろう?」というみなさんのお悩みを解決します!
ぜひ最後までお付き合いください!
Abstract | 棄却サンプリングで簡単に任意の確率分布からのランダムサンプルを得ることができる
棄却サンプリングを用いると、簡単に任意の確率分布に従うランダムサンプルを得ることができます。
確率分布からのサンプリングは、データ解析の多くの場面で必要です。
一様分布や正規分布といった一般的な確率分布であれば、各種ライブラリを用いてサンプリングできますが、実世界のデータではもっと複雑な分布関数や規格化されていない関数からサンプリングを行う必要がある場合もあります。
任意の確率分布からのサンプリング手法には、解析的な手法(逆関数法)と確率的なサンプリングを行う手法があります。
解析的な手法は便利な方法ではありますが、
- 累積分布の逆関数を解析的に求める必要がある
- 目的の分布関数が規格化されている必要がある
など、実際に使う際のハードルもあります。
今回は、確率的なサンプリングを行う方法として棄却サンプリングを紹介します。
棄却サンプリングは、適当な分布関数からランダムサンプリングを行い、それをある確率で採用(棄却)することで、目的の分布関数に従うランダムサンプルを得る手法です。
手順が簡単で、仕組みも直感的に理解しやすく、実装も簡単にできるので実戦に向いた手法です。
棄却サンプリングを使えば、複雑な分布関数であってもランダムサンプルを簡単に得ることができます!
この記事を読んでマスターしましょう!
Background | 任意の確率分布からランダムサンプルを得るには
確率分布からのサンプリングはベイズ推定など、データ解析の多くの場面で必要になります。
一様分布や正規分布といった、一般的な確率分布であれば、ランダムサンプルを得る関数が様々なライブラリに組み込まれているため問題にはなりません。
一方で、実世界のデータには、そのような一般的な確率分布でない関数からサンプリングしたい場面が発生します。
任意の確率分布からのサンプリングが必要な場面
前回の記事では、任意の確率分布からのサンプリングが必要となる場面をご紹介しました。
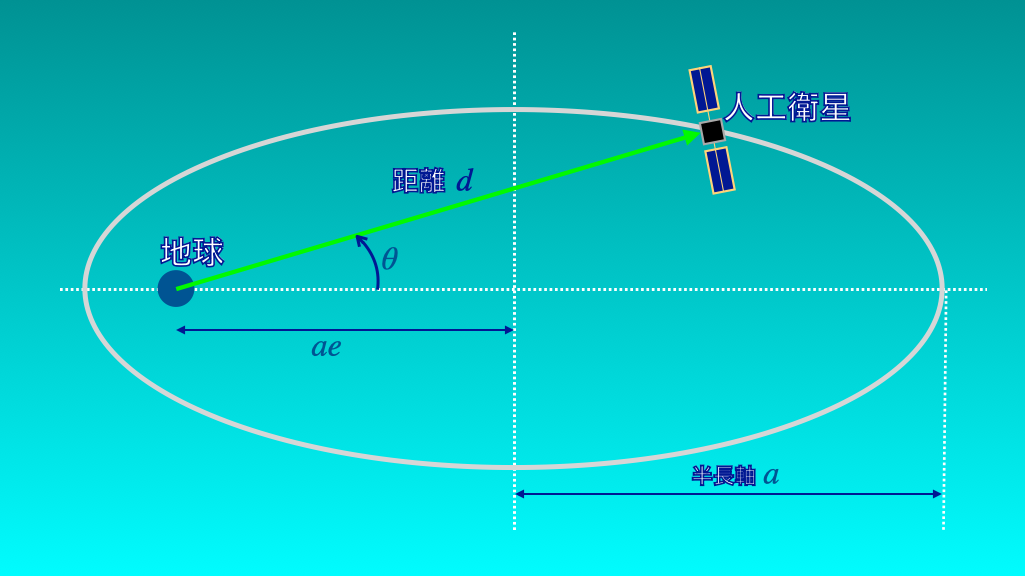
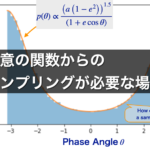
かなりマニアックな例ではありますが、地球を周回する人工衛星の位置(位相角)の分布の例を紹介しました(下図1)。
この位相角\(\theta\)の分布関数\(p(\theta)\)は、
$$
p(\theta) \propto \frac{\left(d_{P} \left(1 + e\right)\right)^{1.5}}{\left(1 + e \cos \theta \right)}
$$
というやや複雑な形をしています(詳細は前回記事参照)。
この分布関数に従うランダムサンプル(乱数)を得るにはどうしたらよいか?というのが今回考えている課題です。
逆関数法によるサンプリングとその限界
任意の確率分布からランダムサンプルを得る解析的な方法として、逆関数法があります。
逆関数法は、目的の確率密度関数について、その累積分布関数の逆関数を得ることができると、一様分布からの変数変換として、目的の確率密度関数に従うランダムサンプルが得られるというものです。
ここでは詳細は割愛しますが、簡単に説明を書いておきます。
累積分布関数は、目的の確率密度関数に従うサンプル\(x\)を[0,1]の一様分布に従うサンプルに変換する関数です。
この逆関数を使うと、[0,1]の一様分布に従うサンプルを、目的の確率密度関数に従うサンプルに変換することができるという仕組みです。
逆関数法は、累積分布関数の逆関数を得ることさえできれば、簡単に所望のランダムサンプルを得ることができ、解釈も容易である良い手法です。
しかし、実際に用いるには、以下の2つの制限があります。
- 累積分布関数の逆関数の解析解を得る必要がある
- 目的の分布関数は、規格化された関数(確率密度関数)である必要がある
実世界のデータでは、これら2つを満たすことが難しい場合が多くあります。
目的の分布関数を積分することが難しく、さらにその逆関数の解析解を得るのも難しいという場合には1を満たすことができません。
もしかしたら方法はあるのかもしれませんが、私は人工衛星の位相角の分布関数\(p(\theta)\)の累積分布関数の逆関数を計算することはできませんでした。
また、目的の分布関数の規格化が行えないということもよくあります。
人工衛星の位相角の分布関数\(p(\theta)\)の式は実は比例式の形でしか求まっていません。
したがって、そもそも規格化定数がどのような値になるのかはよくわかりません。
また、積分を求めるのが関数であれば、やはり規格化は困難です。
任意の確率分布からサンプルを得る確率的なサンプリング手法
このように、逆関数法が使えない場合には、確率的なサンプリング手法が役に立ちます。
今回と次回では2つの確率的なサンプリング手法
- 棄却サンプリング (rejection sampling)
- MHサンプリング (Metropolis-Hastings sampling)
をご紹介します。
棄却サンプリングは、適当な乱数を発生させ、ある確率で採用(棄却)する方法です。
手順が単純で仕組みが直感的に理解しやすく、実装もしやすいという特長があります。
また、MHサンプリングは棄却サンプリングにマルコフ連鎖過程を取り入れたものです。
今回は棄却サンプリングを紹介します!
Method | 棄却サンプリングの手順と仕組み
棄却サンプリングは、「提案分布」と呼ばれる適当な分布関数からランダムサンプルを得て、それをある確率で採用することで、目標する分布(目標分布)からのランダムサンプルを得るアルゴリズムです。
棄却サンプリングの手順
棄却サンプリングは以下の手順で実行されます。
- 目標分布\(P\)を「覆う」ような提案分布\(Q\)を設定する
- 提案分布\(Q\)からランダムサンプル\(x_{i}\)を得る
- \(x_{i}\)を\(\frac{P(x_{i})}{Q(x_{i})}\)の確率で採用する
- ランダムサンプルを複数得たい場合は、所望の数得られるまで1–3を繰り返す
以下で詳しく見ていきましょう。
目標分布\(P\)を覆う提案分布\(Q\)の設定
提案分布\(Q\)は目標分布\(P\)を「覆っている」必要があります。
ここで、目標分布\(P\)は規格化されていなくても構いません。
提案分布\(Q\)が目標分布\(P\)を「覆っている」とは、任意の\(x\)について、
$$
P(x) \leq Q(x)
$$
が成り立つことを意味します。
つまり、\(x\)がどのような値であっても、\(Q(x)\)は\(P(x)\)よりも大きい必要があります。
図2のようなイメージです。

提案分布\(Q\)をどう設定するか?
提案分布\(Q\)は、\(P\)を覆ってさえいれば何でも構いません。
ただし、ランダムサンプルが簡単に得られるような分布である必要があります。
図2の例では、提案分布として、一様分布を定数倍(\(k\)倍)したものを提示しています。
一様分布からランダムサンプルを得るライブラリはいくらでもあるので、簡単にランダムサンプルを得ることができます。
目標分布\(P\)の最大値が得られるか?
図2では、\(k\)を目標分布\(P\)の最大値としています。
ここで問題となるかもしれないのが、目標分布の最大値が得られるか否かです。
今回の記事で示す実装方法(numpyを使わないもの)では、目標分布の最大値が予めわかっている必要があります。
言葉を変えると、最大値が解析的に計算できる必要があります。
図2の例では、最大値は明らかに\(\theta = -\pi\)もしくは\(+\pi\)のときなので簡単です。
最大値が解析的に得られない(どこで最大になるのかわからない)場合には、第4回でご紹介予定のnumpyを用いた実装方法のやり方を使う必要があります。
このやり方では、数値的に最大値が求まれば棄却サンプリングを行うことができるため汎用性の高い実装方法と言えます。
今回ご紹介する実装方法はあくまでも棄却サンプリングの手順と仕組みが理解しやすいよう、シンプルにしているので悪しからず。
より速い実装方法については、第4回をお楽しみに!
提案分布\(Q\)から候補点\(x_{i}\)のサンプリング
提案分布\(Q\)は、ランダムサンプルが簡単に得られる分布を設定しておくことで、そこからのランダムサンプルを簡単に得ることで、候補点\(x_{i}\)が得られます。
図2の例では、一様分布を使っています。
pythonであれば、numpy.randomを使い
import numpy as np
from scipy.constants import pi
t = np.random.uniform(-pi, pi)としてあげれば、候補点\(x_{i}\)を簡単に得ることができます。
候補点\(x_{i}\)の棄却と採用
候補点\(x_{i}\)を\(\frac{P(x_{i})}{Q(x_{i})}\)の確率でサンプルするには、一様分布から得たサンプルと\(\frac{P(x_{i})}{Q(x_{i})}\)を比較するアルゴリズムを使います。
以下のような手順を取ります。
- 0から\(Q(x_{i})\)までの一様分布から値を一つ得る。この値を\(u\)とする。
- \(P(x_{i}) > u\)であれば、x_{i}を採用する。
割と簡単な手順ですね。
ある値を「適当な確率」で採用するかどうか決定するとき、一様分布から得たサンプルと比較するという手法はなかなかおもしろいです。
この手法を知っておくと様々な場面で役立てることができます。
実際、次回第3回で紹介予定のMHサンプリングでもこのアルゴリズムを使います。
所望のサンプル数が得られるまで繰り返す
棄却サンプリングの弱点は、候補点が確率的に採択されるという仕組み上、手順を何回繰り返せば所望のサンプル数得られるのか、予めわからないことです。
プログラミングで実装する際には、「とにかく所望の数得られるまで繰り返す」という書き方をするしかなくなります。
実行するごとに繰り返し回数が変わる、いわゆる確率的プログラミングのような要素が入るので気持ち悪いといえば気持ち悪いかもしれません。
棄却サンプリングの仕組み
棄却サンプリングの仕組みは、直感的でとても単純です。
手順1と2で、提案分布からランダムサンプルを得ると、下図3のように提案分布に従うサンプルが得られます。
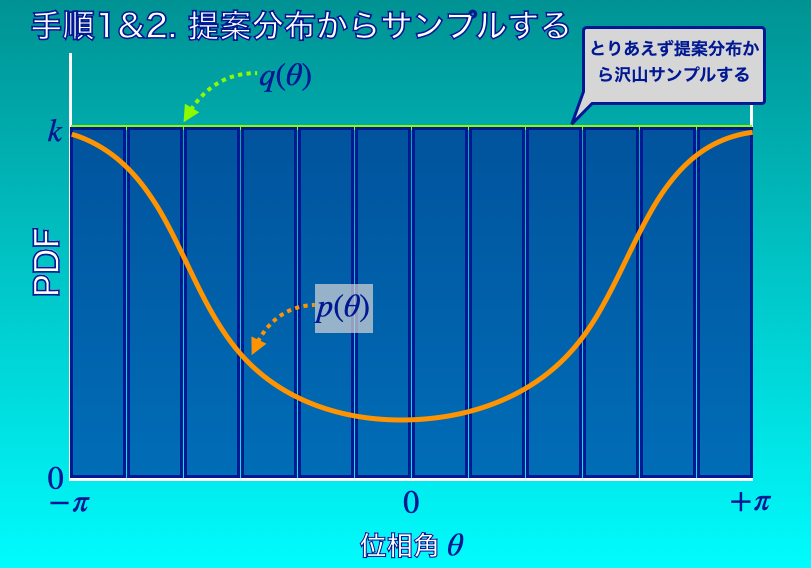
図3の青いヒストグラムは、提案分布に従うランダムサンプル\(\theta_{i}\)をとにかく沢山得たイメージです。
このランダムサンプルを\(\frac{p(\theta_{i})}{q(\theta_{i})}\)の確率で採択していきます。
そのために、まずはそれぞれの\(\theta_{i}\)における\(p(\theta_{i})\)と\(q(\theta_{i})\)を計算します。
\(\theta_{i}\)において、提案分布に従うランダムサンプルは\(q(\theta_{i})\)個(に比例する数)得られているはずです。
このうち、採択したいのは\(p(\theta_{i})\)個(に比例する数)です。
なぜなら、それぞれの\(\theta_{i}\)において、\(p(\theta_{i})\)個(に比例する数)採択できれば、\(p\)に従うランダムサンプルとなるからです。
これを実現するためには、それぞれの\(\theta_{i}\)において、\(\frac{p(\theta_{i})}{q(\theta_{i})}\)の確率で採択してあげれば良いことになります。
提案分布に従うランダムサンプルは\(q(\theta_{i})\)個(に比例する数)得られているわけですから、単純に、そのうち\(p(\theta_{i})\)個(に比例する数)だけ採用すればよいのです。
図にすると、下図4のようになります。
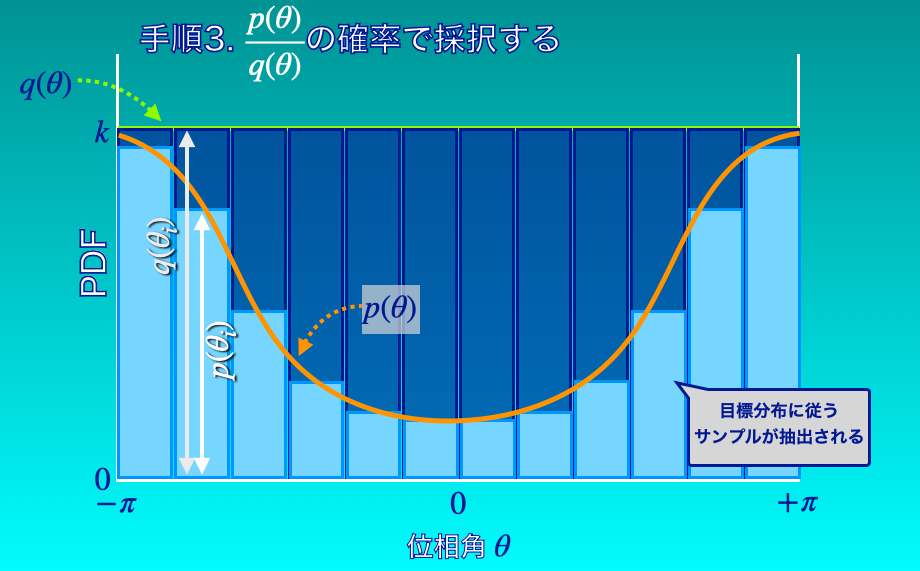
図4の例では、提案分布を一様分布としましたが、他の分布を使った場合も同様です。
それぞれの候補点\(x_{i}\)について、\(q(x_{i})\)個(に比例する数)のサンプルが得られているわけですから、そこから\(p(x_{i})\)個(に比例する数)だけ採択すればよいのです。
この処理は、候補点\(x_{i}\)を確率\(\frac{p(x_{i})}{q(x_{i})}\)で採択するという処理によって実現できます。
Result | pythonでの簡単な実装例
棄却サンプリングの簡単な実装例をご紹介します。
jupyter notebookの例
ソースコードは以下です。
コピー&ペーストして使っていただいて構いませんが、自己責任でご利用ください。
matplotlibはversion3.3.4が必要です(それ以前はhistogramにdensityパラメータがない)。
↓スクロールしてご覧ください。
コーディングのポイント
コーディングのポイントをお話します。
目標分布の定義
目標分布は以下の箇所で定義されています。
# 目標の分布
def p(theta, d=100*1000., e=0.1):
return (d * (1-e**2) / (1-e))**1.5 / (1 + e*np.cos(theta))**2theta(\(\theta\))がこの分布関数の変数です。
dとeはoptional argumentsとして渡します。
単に
$$
p(\theta) \propto \frac{\left(d_{P} \left(1 + e\right)\right)^{1.5}}{\left(1 + e \cos \theta \right)}
$$
を返す関数です。
棄却サンプリングする関数の定義
棄却サンプリングのアルゴリズムは以下の箇所で定義されています。
# 棄却サンプリング
def sampling(d=100*1000., e=0.1):
# get k parameter as max
k = p(pi, d=d, e=e)
# loop until accepted
while True:
# sampling from the proposed distribution
t = np.random.uniform(-pi, pi)
# sampling u from [0, kq(z)]
u = k*np.random.uniform(0, 1.0)
# judge if accept
if(p(t, d=d, e=e) > u):
return tここで、dとeは分布関数pに渡す引数です。
以下の箇所で、提案分布が目的分布を覆うようにするパラメータ\(k\)を計算しています。
関数pの最大値としています。
# get k parameter as max
k = p(pi, d=d, e=e)また、以下の箇所によって、候補点が採択されるまでの繰り返し処理をしています。
# loop until accepted
while True:提案分布\(Q\)から候補点\(x_{i}\)をサンプルするところは以下になります。
\([-\pi, +\pi)\)の一様分布からサンプルします。
ここでは、候補点\(x_{i}\)はtという変数に格納されます。
# sampling from the proposed distribution
t = np.random.uniform(-pi, pi)さらに、候補点\(x_{i}\)の採択可否を判定するための、\([0, k)\)の一様分布からのサンプル\(u\)は以下の箇所で取得します。
# sampling u from [0, kq(z)]
u = k*np.random.uniform(0, 1.0)最後に、\(P(x_i)\)を\(u\)と比較して採択可否を判定します。
\(P(x_i) > u\)であれば、その候補点を採択し、returnで返して関数を終了します。
候補点が採択されなければ、whileループでやり直します。
# judge if accept
if(p(t, d=d, e=e) > u):
return tこのように、Methodのセクションで説明した手順が実装されているのがわかると思います。
サンプリングを行う箇所
棄却サンプリングを行う関数samplingを用いてサンプリング箇所は以下です。
# sampling using rejection sampling
samples = np.array([sampling(d = d, e = e) for i in range(N)])N個のサンプルが返ってくるまで棄却サンプリングを繰り返し、結果がnumpy arrayとして格納されます。
この実装方法の注意点 | ループを回すために遅い
この実装方法の注意点は計算時間がかかることです。
whileループで繰り返し処理をするためにとても遅いです。
pythonのようなスクリプト言語は、c言語のようなコンパイル言語と比べてループ処理が苦手です。
説明は省きますが、pythonで繰り返し処理を高速実装するには、numpyなど、裏側でコンパイル言語が動くライブラリを使う必要があります。
今回の例では、100万サンプルを得るのに30秒ほどかかりました。
第4回で紹介予定のnumpyを用いた実装では0.5秒で済みます。
pythonでループ処理を行うのが、大きなタイムロスを引き起こすことがよくわかります。
ちなみに計算時間は実行環境によります。
またまた、ちなみにpythonのバージョンによっては8秒ぐらいになったりもします。
私の場合は、python 3.6だと8秒、3.7だと30秒でした。
python本体以外にも付属ライブラリのバージョンによっても変わりそうですが、同じ計算機でも、バージョンによってこれだけ計算時間が変わるのは興味深いです。
Conclusion | まとめ
最後までご覧いただきありがとうございました!
任意の分布からランダムサンプルを得る方法として「棄却サンプリング」のやり方と実装例をご紹介しました!
棄却サンプリングは、
- 逆関数法など変数変換によるサンプリングを行うには関数系が複雑な場合
- 規格化されていない(分布関数の積分が1にならない)場合
にランダムサンプリングを得る方法です。
その仕組も直感的にわかりやすく、実装もしやすいので知っておくと便利です!
第4回ではより高速な実装方法もご紹介しますので、そちらもお楽しみに!
以上「統計学&pythonレシピ | 任意の確率分布からのサンプリング2(棄却サンプリング導入編)」でした!
またお会いしましょう!Ciao!

コメント