統計学レシピ｜正規分布を超えたいあなたに捧げるJohnsonのSU分布(実践編）

Ciao！みなさんこんにちは！このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信していきます。

今回はpythonデータ解析編、知っていると便利な確率分布、JohnsonのSU分布の第3回、実践編です！
実践編では、pythonを使って、JohnsonのSU分布の作図例や、実際のデータへのフィット例をご紹介します！
いよいよ本シリーズ最終回です！
お楽しみください！

第1回の導入編ではJohnsonのSU分布が必要になる現実のデータの例を、第2回の基礎編ではJohnsonのSU分布の確率密度関数、そのパラメータを変化させると分布の形がどう変わるかなどの性質をご紹介しました。
まだ導入編と基礎編を見ていない方は、ぜひそちらも御覧ください！
導入編: https://the-silkworms.com/ds_stat_johnsons-su_intro/94/
基礎編: https://the-silkworms.com/ds_stat_johnsons-su_basic/160/

Abstract | pythonではscipyを使ってJohnsonのSU分布を実装できる
Method | scipy.stats.johnsonsuを使う
1. scipy.stats.johnsonsuの基本
2. scipy.stats.johnsonsuでできること
Result | JohnsonのSU分布の当てはめ
Conclusion | まとめ
References | 参考

Abstract | pythonではscipyを使ってJohnsonのSU分布を実装できる

pythonでは、科学計算ライブラリscipyを利用して、JohnsonのSU分布に関連するフィッティングや統計値の計算を簡単に行うことができます。
scipyのstatsモジュールのjonsonsuという関数を利用して、確率分布の描画、平均値、中央値、パーセンタイル値、期待値の計算をすることができます。
また、scipyのフィッティングアルゴリズムや最小化アルゴリズムと組み合わせて、最尤推定による観測データの母集団推定、ヒストグラムのフィッティングなど、データサイエンスの現場で遭遇する課題にも対応できます。

Method | scipy.stats.johnsonsuを使う

pythonにはscipyという科学計算ライブラリが用意されています。
その中にstatsというモジュールがあり、そこにjohnsonsuという関数が用意されています。
次のようなコードを書くと、呼び出すことができます。

# scipyとstatsモジュールのインポート
import scipy
from scipy.stats import johnsonsu
# johnsonsuの使用
rv_jsu = scipy.stats.johnsonsu(0.0, 1.0, loc = 0.0, scale = 1.0)

scipy.stats.johnsonsuの基本

scipyの英語のマニュアルはこちらにあります。
このライブラリの使い方として、いくつかパターンがあります。
scipy.stats.johnsonsuは”johnsonsu_gen”というobjectを返します。
このobjectを作っておいて、必要なときに確率分布や累積分布関数を呼び出すのが便利です。
詳しくは次のセクションで説明します。

scipy.stats.johnsonsuは$a, b, \mathrm{scale}, \mathrm{loc}$の4つのパラメータで制御します。
それぞれ、基礎編で定義した$\gamma, \delta, \xi, \lambda$と同じです。
$\gamma = 0, \delta = 1, \xi = 0, \lambda = 1$の場合は、

rv_jsu = scipy.stats.johnsonsu(0.0, 1.0, loc = 0.0, scale = 1.0)

または

rv_jsu = scipy.stats.johnsonsu(0.0, 1.0, 0.0, 1.0)

のようにして、”johnsonsu_gen”objectを作ってあげます。
ここでは”rv_jsu”というパラメータに格納しました。

scipy.stats.johnsonsuでできること

“johnsonsu_gen”objectを作ると、そこから様々なmethodを呼び出すことができます。
代表的なものをあげると、以下のようなことができます。

pdf: 確率分布関数
logpdf: 確率分布関数をlog変換したもの(最尤法で使える)
cdf: 累積分布関数
ppf: 累積分布関数の逆関数(percentile point functionの略)
expect: 確率加重した期待値
median: 中央値
mean: 平均値
std: 標準偏差

他にもたくさんありますので、scipyのマニュアルをご参照ください。

例えば、xにおける確率を求めたいときには以下のようにします。

x = 0.0
prob_x = rv_jsu.pdf(x)

実際にデータ解析をする際の使い方については、次のResultのセクションをご覧ください！

Result | JohnsonのSU分布の当てはめ

ここからは、導入編、基礎編で取り上げた例で、scipyを使ったJohnsonのSU分布の実装をマスターしましょう！
実際にpython (jupyter notebook)のコードを掲載します！
みなさんがpythonでデータ解析をする際にご参照ください！
コピー&ペーストして使っていただいて結構です！
＊ソースコードに間違いがあっても責任は取りかねますので、自己責任でご利用ください。

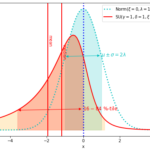
JonsonのSU分布と正規分布を比較する

基礎編で図を表示した、JohnsonのSU分布と正規分布の比較です。

実際のソースコード

まずは実際のソースコードを御覧ください。

pythonコードのポイント

「分布形状をプロットする関数」という箇所で、”pdist_plot[t]”というdict変数にjohnsonsu_gen objectを格納しています。

pdist_plot[t] = sp.stats.johnsonsu(p_su[0], p_su[1], loc = p_su[2], scale = p_su[3])

また、「統計値を取得する関数」の中で、平均(mean), 中央値(median), 標準偏差(std), パーセンタイル(%-tile)を計算しています。

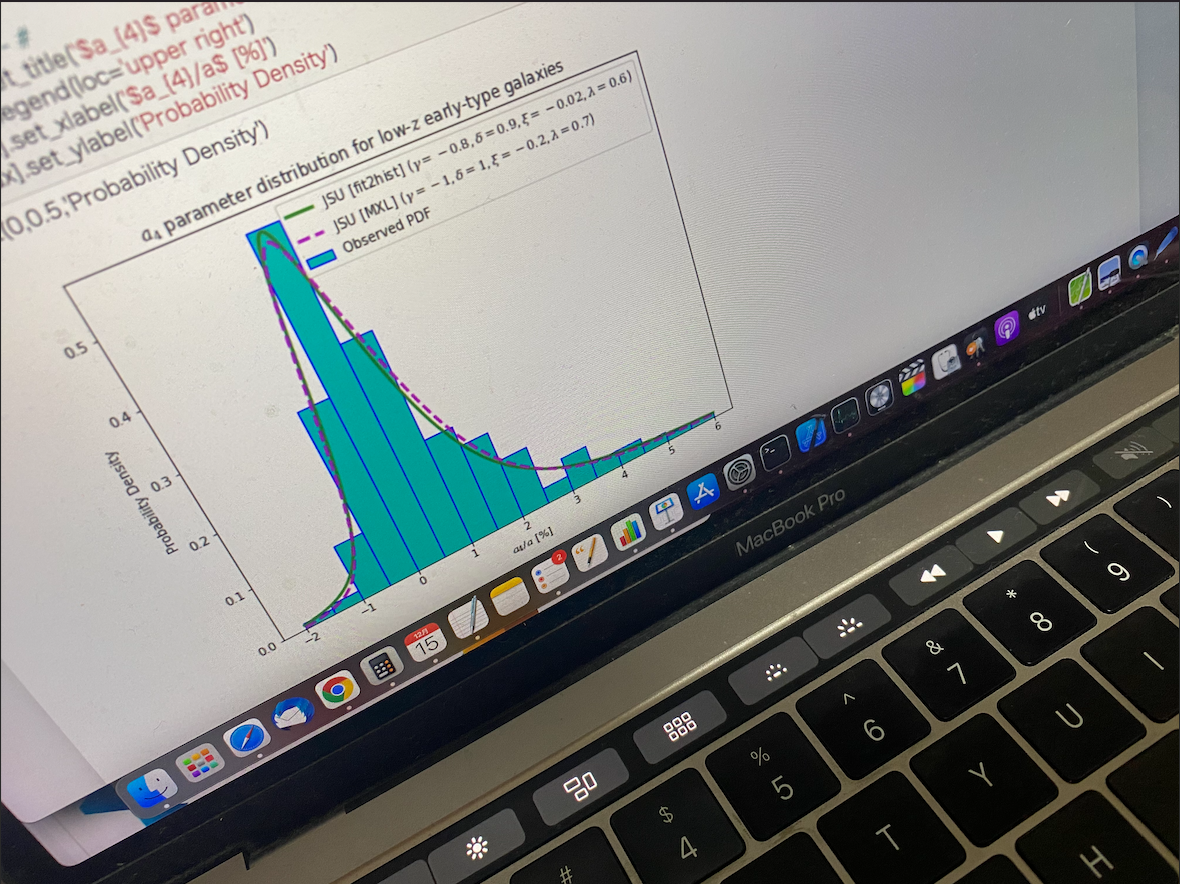
楕円銀河の$a_{4}$パラメータの分布にSU分布をフィットする

次に、導入編でJohnsonのSU分布が必要になる例として挙げた、楕円銀河の$a_{4}$パラメータの分布の例です。
$a_{4}$パラメータの意味については導入編を御覧ください。

実際のソースコード

まずは実際のソースコードです。以下を御覧ください。
また、入力データの$a_{4}$パラメータのファイルはこちらです。

a4_Ms_L ダウンロード

pythonコードのポイント

「3. ヒストグラムを作ってSU分布をフィットする」では、まずは$a_{4}$のヒストグラムを作成し、それに対してJohnsonのSU分布の確率分布関数を当てはめて（フィットして）います。
フィットにはscipy.optimizeというmoduleのcurve_fitという関数を使っています。
文字通り、$y=f(x)$という曲線をフィットさせる関数です。
curve_fitの詳しい使い方は今回は解説しませんが、興味のある方はscipyのマニュアルを見てください。

「4. 最尤法でSU分布をフィットする」では、観測された$a_{4}$の分布が、最も尤もらしく再現されるようなJohnsonのSU分布のパラメータを求めています。
いわゆる最尤推定というやりかたです。
前述の「3. ヒストグラムを作ってSU分布をフィットする」の結果とは少し異なる結果が得られます。
今回の目的に照らせば、最尤推定の方が素直なやり方です。

ここでは、logpdfというmethodを使って、対数尤度の和を計算しています。

# - get log pdf array- #
logpdf_ary = sp.stats.johnsonsu.logpdf(x_s, p_s[0], p_s[1], loc = p_s[2], scale = p_s[3])
# - return residual - #
return - np.sum(logpdf_ary)

対数尤度の和は、Johnson SU分布が与えられたとき、観測された$a_{4}$のデータセットが実現する確率の対数になります。
\(a_{4})のデータセットが実現する確率は、
$$(データ点1が実現する確率) \times (データ点2が実現する確率) \times \dots \times (データ点Nが実現する確率)$$
のように確率の積になりますが、対数を取ることで和として扱うことができます。

最尤法では、対数尤度が最大になるように、Johnson SU分布の4つのパラメータを決定します。
意味合いとしては、観測された(\a_{4})のデータセット(統計学用語で言う標本分布)が最も実現されやすいJohnson SU分布(母集団分布)を推定していることになります。

また、scipy.optimizeのfminという関数でパラメータを推定したいので、np.sum()にマイナスがついています。
fminは、ある関数の最小値を与えるパラメータを探してくれる関数です。

GDP成長率予測値の分布にJohnsonのSU分布をフィットする

最後に、導入編で紹介した例をもう一つ。
Tさんのお悩み課題であった、GDP成長率予測値の分布にJohnsonのSU分布をフィットする例です。
フィットしたSU分布を使って、25 %-tile以下における期待値を計算します。

実際のコード

まずは以下の実際のコードを御覧ください。

pythonコードのポイント

「2. 問題設定」では、導入編で掲載した図を作成しています。
まず、観測値（調査機関によるアンケート集計結果）を設定しています。

# GDP成長率の予測値の集計結果
x1 = (100.-np.array([4, 10, 50, 75, 90, 96])) / 100. # %-tile
y1 = np.array([7.9, 5.9, 2.6, 1.4, -1.9, -4.3]) # GDP成長率予測値[%]

パーセンタイル点であるx1を、100の補数として定義しています。
何故か集計結果が値の大きな方からパーセンタイル点を数えていたためです。
そのままだと、scipy.stats.johnsonsuのppf()メソッドが上手く動かないので、パーセンタイル点を小さい方から数えるように変換しています。

「3. SU分布のフィット」では、%-tile点と%-tile値にJohnsonのSU分布をフィットしています。
ここで、

累積分布関数から出力される値（GDP成長率予測値を入力して得られる%-tile点）をフィットする
ppf関数から出力される値（%-tile点を入力して得られるGDP成長率予測値）をフィットする

という2通りの方法があります。
後者のほうがplotしたときに、当てはまりが良さそうに見えたので、こちらを採用しました。
興味がある方は、前者を採用した場合と比較してみてください。ソースコードの

p_opt = sp.optimize.fmin(func_to_min_JSU_ppf, p_init, args=(y1, x1), disp = True)

を

p_opt = sp.optimize.fmin(func_to_min_JSU_cdf, p_init, args=(y1, x1), disp = True)

に変更することで試すことができます。

「4. 25 %-tile以下期待値の計算」では、得られたJohnsonのSU分布を使って、25 %-tile以下期待値を計算しています。
“johnsonsu_gen” objectからexpectというmethodを呼び出して計算しています。
このmethodでは第1引数に関数を指定でき、以下の積分が計算されます。
$$\int_{\mathrm{lb}}^{\mathrm{ub}}{f(x)\ \mathrm{pdf}(x) dx}$$
$\mathrm{lb}, \mathrm{ub}$で積分区間を指定できます。指定しない場合は($-\infty, \infty$)となります。

第1引数を指定しない場合には、$f(x)=x$となり、単に期待値が計算されます。
今回はこのやりかたを実施しています。