Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
今回はPythonデータ解析、NumPy配列の要素同士の全ての組み合わせについて計算を行う方法をいくつか紹介し、計算速度を比較します。例えば、2つの配列の要素同士の全ての組み合わせについて差分をとるケースです。ここでは、np.ufunc.outer()を使う方法、np.meshgrid()やnp.tile()で高次元化する方法を比較します。
この記事を読めば、配列の要素同士の全ての組み合わせについて計算に高速する方法がわかります。

この記事はこんな人におすすめ
- Pythonでデータ解析をしている
- Numpyの配列計算を高速にしたい
Abstract | 要素同士の全ての組み合わせ計算はnp.ufunc.outerで
NumPy配列の計算で、2つの配列の要素同士の全ての組み合わせについて、加算や減算などの計算を行いたい場面では、np.ufunc.outerを使うと高速に計算できます。例えば、1次元配列\(a = [a_{1}, a_{2}, \dots, a_{n}]\)と1次元配列\(b = [b_{1}, b_{2}, \dots, b_{m}]\)があるとき、\(a\)の各要素について最も近い\(b\)の要素を取り出したい場合には、要素同士の全ての組み合わせについての差分\(a_{i} – b_{j}\)を得る必要があります。このような場合には、np.subtract.outer(a, b)を使うと一発で計算できる上、計算も高速です。np.ufunc.outerはufuncの部分をNumPyのuniversal function(略称ufunc)として定義されている様々な四則演算やその他の演算にすることができます。要素同士の全ての組み合わせについて様々な計算ができます。outerメソッドを使いこなして高速計算していきましょう!
Background | 配列の要素の全ての組み合わせについての計算
今回行いたいことは、配列\(A = [ \vec{a_{1}}, \vec{a_{2}}, \dots, \vec{a_{n}} ] \)と配列\(B = [\vec{b_{1}}, \vec{b_{2}}, \dots, \vec{b_{m}}]\)があるとき、要素ごとの計算\( f( \vec{a_{i}}, \vec{b_{j}} ) \)を全て要素の組み合わせについて計算することです。
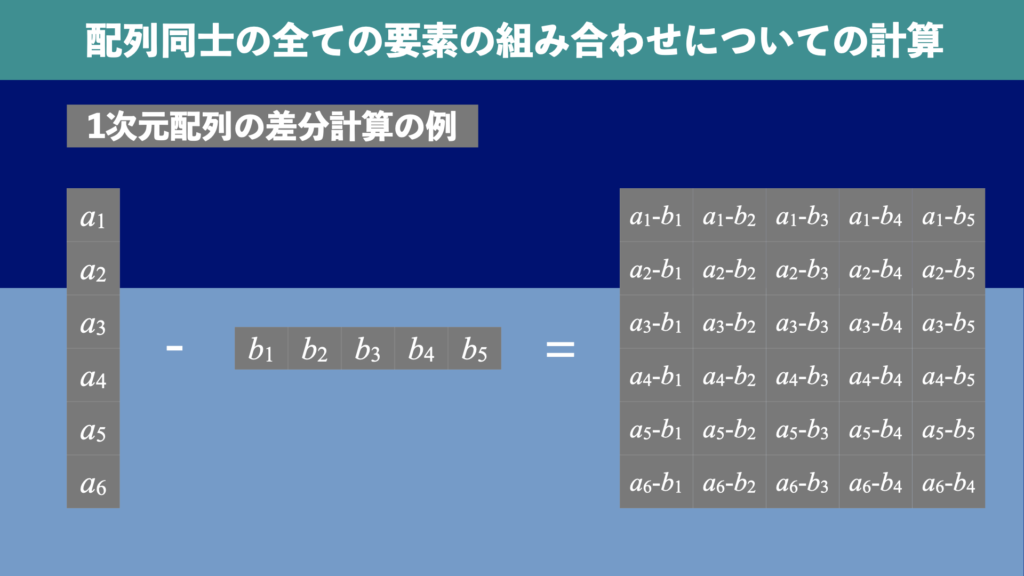
例えば、1次元配列(すなわちベクトル)\(A = [a_{1}, a_{2}, \dots, a_{n}]\)と\(B = [b_{1}, b_{2}, \dots, b_{m}]\)が与えられたとき、要素同士の全ての組み合わせについての差分
$$
\left(
\begin{matrix}
a_{1} – b_{1} & a_{1} – b_{2} & \dots & a_{1} – b_{m} \\
a_{2} – b_{1} & a_{2} – b_{2} & \dots & a_{2} – b_{m} \\
\dots & \dots & \dots & \dots \\
a_{n} – b_{1} & a_{n} – b_{2} & \dots & a_{n} – b_{m}
\end{matrix}
\right)
$$
の計算を行うことを考えます(図1)。
Pythonでやってはいけない計算方法 | ループ処理
まず思いつくのは、ループ処理で計算することです。例えば、以下のように書けば、上記の例の計算を実装することができます。
# prepare arrays
a = np.arange(6)
b = np.arange(4)
# loop
c = np.zeros([len(a), len(b)])
for i in range(len(a)):
for j in range(len(b)):
c[i, j] = a[i] - b[j]しかし、Pythonのループ処理は非常に遅いです。NumPy配列を使う場合、NumPyに対応した計算方法を使うことで高速に計算することができます。ループ処理をしてしまうと、このようなNumPy配列を使うメリットがなくなってしまいます。NumPy対応の方法と比べてPythonのループがどのくらい遅いかについては、過去記事「NumPyレシピ | np.exp(x)はe**xよりも2倍ほど高速!」をご参照ください。
NumPy対応の方法で全ての組み合わせについて計算を行う方法3つ
NumPy対応で、2つの配列の要素の全ての組み合わせについて計算を行う方法は大きく分けて2つ
np.ufunc.outer()を使う方法- 高次元の配列を経由する方法
があります。後者の高次元の配列を経由する方法では高次元の配列の作り方が2つあるため、全部で3つ
np.ufunc.outer()を使う方法np.meshgrid()を使う方法(高次元配列を経由)np.tile()を使う方法(高次元配列を経由)
が存在します。
np.ufunc.outer() | NumPyの標準的な関数で使える方法
np.ufunc.outer()はNumPyで用意されている標準的な関数(universal function、略称ufunc)について用意されているメソッドです。np.ufunc.outer()はNumPyのufuncとして定義された関数を、全ての要素の組み合わせについて行うメソッドです。Numpyのufuncとしては四則演算
- np.add(): 加算
- np.subtract(): 減算
- np.multiply(): 乗算
- np.divide(): 除算
や数学的な計算
- np.power(x1, x2): x1のx2乗
- np.log(): 自然対数
- np.sin(): 三角関数
などが用意されています。Numpyのufuncについて詳しくはこちらのNumPyのマニュアルページをご覧ください。
- Universal functions (ufunc): https://numpy.org/doc/stable/reference/ufuncs.html
今回やりたいことは、基本的にはnp.ufunc.outer()を使えば実現可能です。例えば、次元配列\( a = [a_{1}, a_{2}, \dots, a_{n}]^{T}\)と\(b = [b_{1}, b_{2}, \dots, b_{m}]\)が与えられたとき、配列aとbの要素同士の全ての組み合わせについての差分、
np.subtract.outer(a, b)は\(n \times m\)の2次元配列
$$
\left[
\begin{matrix}
a_{1} – b_{1}, a_{1} – b_{2}, \dots, a_{1} – b_{m} \\
a_{2} – b_{1}, a_{2} – b_{2}, \dots, a_{2} – b_{m} \\
\dots \\
a_{n} – b_{1}, a_{n} – b_{2}, \dots, a_{n} – b_{m}
\end{matrix}
\right]
$$
を返します。生成される配列のサイズは0次元目が1つ目の配列の長さ\(n\)、1次元目が1つ目の配列の長さ\(m\)となります。
他の四則演算についても同様に、ufuncの後にouterをつけて実行します。np.ufunc.outer()について、詳しいマニュアルはこちらのNumPyページをご覧ください。
np.meshgrid() | 配列を高次元化する方法1
np.meshgrid()を使うと、配列を高次元化することができます。例えば、1次元配列\( a = [a_{1}, a_{2}, \dots, a_{n}]^{T}\)と\(b = [b_{1}, b_{2}, \dots, b_{m}]\)が与えられたとき、
b_2d, a_2d = np.meshgrid(b, a)とすれば、\(n \times m\)の2次元配列が得られます。得られる配列は
$$
b_{\mathrm{2d}} =
\left[
\begin{matrix}
b_{1}, b_{2}, \dots, b_{m} \\
b_{1}, b_{2}, \dots, b_{m} \\
\dots \\
b_{1}, b_{2}, \dots, b_{m}
\end{matrix}
\right]
$$
と
$$
a_{\mathrm{2d}} =
\left[
\begin{matrix}
a_{1}, a_{1}, \dots, a_{1} \\
a_{2}, a_{2}, \dots, a_{2} \\
\dots \\
a_{n}, a_{n}, \dots, a_{n}
\end{matrix}
\right]
$$
となります。np.func.outerの返り値と配列のサイズ(axisの順番)を合わせるには、np.meshgrid()の引数はb, aのようにbを先にする必要があります。個人的には、axisの順番のわかりにくさがnp.meshgrid()の弱点だと思います。
np.meshgrid()によって2次元配列a_2dとb_2dが得られたら
a_2d - b_2dとすれば、目的である要素同士の全ての組み合わせの差分が得られます。結果は
np.subtract.outer(a, b)と同じです。
np.tile() | 配列を高次元化する方法2
np.tile()を使うと、配列を高次元化することができます。引数を「どの軸に何回繰り返すか」という形式で与えられるので、np.meshgrid()よりも生成される配列の形式がわかりやすいです。例えば、1次元配列\( a = [a_{1}, a_{2}, \dots, a_{n}]^{T}\)と\(b = [b_{1}, b_{2}, \dots, b_{m}]\)が与えられたとき、
a_2d = np.tile(a[:,None], (1, m))
b_2d = np.tile(b[None,:], (n, 1))とすれば、\(n \times m\)の2次元配列a_2dとb_2dが得られます。1つ目の引数に高次元化したい配列を取ります。配列を拡大したい軸のインデックスにNoneと書き、他は:とします。2つ目の引数にどの軸に何回繰り返すかを指定します。(1, m)とすれば、0番目のaxisには繰り返しなし(長さnのまま)、1番目のaxisにm回繰り返す、すなわち出来上がる配列は[n, m]となります。得られる2次元配列はnp.meshgrid()のときと同じで、
$$
a_{\mathrm{2d}} =
\left[
\begin{matrix}
a_{1}, a_{1}, \dots, a_{1} \\
a_{2}, a_{2}, \dots, a_{2} \\
\dots \\
a_{n}, a_{n}, \dots, a_{n}
\end{matrix}
\right]
$$
と
$$
b_{\mathrm{2d}} =
\left[
\begin{matrix}
b_{1}, b_{2}, \dots, b_{m} \\
b_{1}, b_{2}, \dots, b_{m} \\
\dots \\
b_{1}, b_{2}, \dots, b_{m}
\end{matrix}
\right]
$$
となります。
np.tile()によって2次元配列a_2dとb_2dが得られたら
a_2d - b_2dとすれば、目的である要素同士の全ての組み合わせの差分が得られます。結果は
np.subtract.outer(a, b)と同じです。
Method | 要素同士の全組み合わせ計算の3手法で計算速度を測定する
さて、実際にJupyter Notebookでコードを書き、2つのNumPy配列についての要素同士の全組み合わせを計算するの3手法
np.ufunc.outer()で計算する方法np.meshgrid()で高次元化してから計算する方法np.tile()で高次元化してから計算する方法
を実装し、計算速度を測定していきます。
今回は例として、2つの配列は1次元とし、要素同士の全組み合わせの差分を計算する場合を扱います。
準備 | ライブラリ、変数x、関数群
まずは、
- 必要なライブラリのインポート
- 計算に用いられる関数群の準備
をしていきます。
ライブラリのインポート
まずは必要なライブラリをインポートします。Jupyter Notebookのコードセルで以下を実行します。
import sys
import numpy as np
import time当然NumPyを使うのでnpとしてインポートしておきます。timeライブラリは計算時間の測定に使います。sysライブラリは実行中の関数名の表示に使います。
関数の準備
あとで呼び出して使えるように関数を準備しておきます。
- 2つの配列を作る関数
のxつの関数を作っておきます。
2つの配列を作る関数
2つの1次元配列を作る関数を定義しておきます。配列の長さn1, n2を引数とし、1次元配列2つを返します。1次元配列の内容は標準正規分布に従うランダムな数値とします。以下を実行します。
# get p and q
def get_2arrays_1d(n1: int, n2: int) -> tuple:
"""
arguments:
n1 <int>: number of sample A
n2 <int>: number of sample B
returns:
p <2d array [n1,m]>: points in sample A
q <2d array [n2,m]>: points in sample B
"""
p = np.random.normal(size=[n1])
q = np.random.normal(size=[n2])
return p, qちなみに、この関数定義は「型注釈」つきで定義しています。型注釈をつけない場合、関数の冒頭は
def get_2arrays_1d(n1, n2):となります。型注釈は任意ですが、つけておくと引数や返り値の型がわかりやすいです。
時間を測定する関数
処理を複数回実行して時間を測定する関数を用意しておきます。以下を実行します。
# measure runtime
def mes_run_time(fnc, *args, n=5):
# time array
t_dat = np.zeros([n])
# loop for n
for i in range(n):
# get start UNIX time
t0 = time.time()
# run process
ret = fnc(*args)
# get end time
t1 = time.time()
# to array
t_dat[i] = (t1-t0)
# - show result - #
print(' results:', ret.ravel()[:3])
# - avg, std - #
t_avg = np.average(t_dat)
t_std = np.std(t_dat)
# - verb - #
print(' delta t [s] = %f +/- %f' % (t_avg, t_std))
# - end - #
return t_avg, t_stdこの関数は過去記事
で既出なので詳細は割愛します。fnc(*args)をn回実行して、計算時間の平均と標準偏差を返します。
np.ufunc.outerを使って全組み合わせの差分を計算する関数
np.ufunc.outerを使って、2つの1次元配列の要素同士の全ての組み合わせの差分を計算する関数を定義します。np.ufunc.outerを実行するだけですが、np.meshgridやnp.tileを使う場合の関数(後述)と引数の形式をあわせるために関数を定義しておきます。以下を実行します。
# get difference between p and q
def get_diff_outer(
p: np.array,
q: np.array,
verb=True
) -> np.array:
"""
arguments:
p <1d array [n1]>: points in sample A. n1 for number of sample, m for dimension.
q <1d array [n2]>: points in sample B. n2 for number of sample, m for dimension.
verb <bool>: print
returns:
d_2d <2d array [n2,n1]>: sqare distance betweem p and q
"""
# - current frame - #
if verb:
print(" - %s -" % (sys._getframe().f_code.co_name))
# - time measurement - #
t0 = time.time()
# - get diff 0 #
d_2d = np.subtract.outer(q, p)
if verb:
print(' size of d_2d: %.3g MB' % (sys.getsizeof(d_2d)/10**6))
# - time measurement - #
t1 = time.time()
if verb:
print(
' time for %s: %f sec'
% (sys._getframe().f_code.co_name, (t1 - t0))
)
# - end - #
return d_2d引数pとqの要素の全ての組み合わせについての差分\((q_{i}) – p_{j}\)を計算します。
np.meshgridを使って全組み合わせの差分を計算する関数
np.meshgridを使って相互差分を計算する関数を定義します。以下を実行します。
# get diff btw p and q
def get_diff_meshgrid(
p: np.array,
q: np.array,
verb=True
) -> np.array:
"""
arguments:
p <1d array [n1]>: points in sample A. n1 for number of sample, m for dimension.
q <1d array [n2]>: points in sample B. n2 for number of sample, m for dimension.
verb <bool>: print
returns:
d_2d <2d arrau [n2,n1]>: sqare distance betweem p and q
"""
# - current frame - #
if verb:
print(" - %s -" % (sys._getframe().f_code.co_name))
# - time measurement - #
t0 = time.time()
# - set params - #
n1 = len(p)
n2 = len(q)
# - get 2d array - #
p_2d, q_2d = np.meshgrid(p, q) # <2d array [n2,n1]>
if verb:
print(' size of p_2d: %.3g MB' % (sys.getsizeof(p_2d)/10**6))
print(' size of q_2d: %.3g MB' % (sys.getsizeof(p_2d)/10**6))
# - get diff as 2d array - #
d_2d = q_2d - p_2d # <2d array [n1,n2]>
if verb:
print(' size of d2_2d: %.3g MB' % (sys.getsizeof(d_2d)/10**6))
# - time measurement - #
t1 = time.time()
if verb:
print(
' time for %s: %f sec'
% (sys._getframe().f_code.co_name, t1 - t0)
)
# - end - #
return d_2d引数、返り値ともにget_diff_outer()と全く同じです。途中で2次元配列p_2dとq_2dを生成するところが異なります。
np.tileを使って全組み合わせの差分を計算する関数
np.tileを使って高次元配列を作った上で相互差分を計算する関数を定義します。以下を実行します。
# get distance to q from p
def get_diff_tile(
p: np.array,
q: np.array,
verb=True,
) -> np.array:
"""
arguments:
p <1d array [n1]>: points in sample A. n1 for number of sample, m for dimension.
q <1d array [n2]>: points in sample B. n2 for number of sample, m for dimension.
print_size <bool>: print size of generated arrays
del_array <bool>: delete needless arrays
returns:
d2_2d <2d arrau [n2,n1]>: sqare distance betweem p and q
"""
# - current frame - #
if verb:
print(" - %s -" % (sys._getframe().f_code.co_name))
# - time measurement - #
t0 = time.time()
# - set params - #
n1 = len(p)
n2 = len(q)
# - get 2d array - #
p_2d = np.tile(p[None, :], (n2, 1)) # <2d array [n2,n1]>
q_2d = np.tile(q[:, None], (1, n1)) # <2d array [n2,n1]>
if verb:
print(' size of p_2d: %.3g MB' % (sys.getsizeof(p_2d)/10**6))
print(' size of q_2d: %.3g MB' % (sys.getsizeof(p_2d)/10**6))
# - get difference of the 2d arrays - #
d_2d = q_2d - p_2d # <2d array [n2,n1]>
if verb:
print(' size of d_2d: %.3g MB' % (sys.getsizeof(d_2d)/10**6))
# - time measurement - #
t1 = time.time()
if verb:
print(
' time for %s: %f sec'
% (sys._getframe().f_code.co_name, (t1 - t0))
)
# - end - #
return d_2dこちらも引数と返り値は他2つの関数と同じです。2次元配列の生成方法がnp.tileとなっています。
時間の測定
要素同士の全ての組み合わせについての差分について、
1. np.ufunc.outer()で計算する
1. np.meshgrid()で高次元化してから計算する
1. np.tile()で高次元化してから計算する
のそれぞれで、計算時間を測定し、どの方法が最も高速か考えます。
1次元配列pとqの準備
まずは1次元配列pとqを用意する。どちらも20000個の配列とします。以下を実行します。
# get p and q
p, q = get_2arrays_1d(20000, 20000)これで、2万個の要素の1次元配列pとqが生成されました。
np.ufunc.outerの場合: 0.32 +/- 0.02 秒
np.ufunc.outerを使った場合の差分計算の計算時間を測定します。以下を実行します。
# np.ufunc.outer
_ = mes_run_time(get_diff_outer, *(p, q, False), n=5)実行結果は
results: [ 1.18396436 -0.23789667 0.4614096 ] delta t [s] = 0.313971 +/- 0.015705
となります。計算時間は0.32 +/- 0.02 秒となりました。先に結論を言うと、この方法が3つの中で最も高速です。
なお、pとqがランダムのため、「results:」内容は実行するたびに変わります。ただし、pとqの中身を変更しない限りは変わりません。
np.meshgridの場合: 1.01 +/- 0.02 秒
np.meshgridを使った場合の差分計算の計算時間を測定します。以下を実行します。
# np.meshgrid
_ = mes_run_time(get_diff_meshgrid, *(p, q, False), n=5)結果は
results: [ 1.18396436 -0.23789667 0.4614096 ]
delta t [s] = 1.018840 +/- 0.018963となりました。1.02 +/- 0.02 秒なので、np.ufunc.outerを使うよりも遅いです。
np.tileの場合: 1.82 +/- 0.02 秒
np.tileを使った場合の差分計算の計算時間を測定します。以下を実行します。
# np.tile
_ = mes_run_time(get_diff_tile, *(p, q, False), n=5)結果は、
results: [ 1.18396436 -0.23789667 0.4614096 ] delta t [s] = 1.818672 +/- 0.024048
となりました。1.82 +/- 0.02 秒です。3つの方法の中で最も遅い結果となりました。
(おまけ)メモリ消費量の比較 | np.meshgridとnp.tileの違い
2次元配列を経由する方法では、途中で生成される2次元配列の分だけ余計にメモリを消費します。np.meshgridとnp.tileの挙動の差異が興味深いのでご紹介します。結論を書くと以下のような違いがあります。
- np.meshgrid: 生成される高次元配列のメモリが実際に確保される
- np.tile: 生成される高次元配列のメモリは確保されない(元の1次元配列を参照する)
以下では実際にメモリ消費量を確かめていきます。
np.ufunc.outerの場合のメモリ消費量
np.ufunc.outerを使う方法では明示的な追加メモリの消費は発生しません。np.ufunc.outerを動かす関数get_diff_outerで生成されるのは
- 計算結果を格納する
d_2d: 3.2 GB
となります。これを実際に確かめます。以下を実行してみましょう。
# np.ufunc.outer
_ = get_diff_outer(p,q,verb=True)結果は
- get_diff_outer - size of d_2d: 3.2e+03 MB time for get_diff_outer: 0.285279 sec
となります。
np.meshgridの場合のメモリ消費
np.meshgridを使う方法では、
- 配列
pの2次元化p_2d: 3.2 GB - 配列
qの2次元化q_2d: 3.2 GB - 計算結果を格納する
d_2d: 3.2 GB
の分、メモリが消費されます。以下を実行して確かめてみます。
# np.meshgrid
_ = get_diff_meshgrid(p,q,verb=True)結果は
- get_diff_meshgrid - size of p_2d: 3.2e+03 MB size of q_2d: 3.2e+03 MB size of d2_2d: 3.2e+03 MB time for get_diff_meshgrid: 0.966348 sec
となります。
np.tileの場合のメモリ消費
np.tileを使う方法では、
- 配列
pの2次元化p_2d: 0.000128 GB - 配列
qの2次元化q_2d: 0.000128 GB - 計算結果を格納する
d_2d: 3.2 GB
のとなります。p_2dとq_2dの分のメモリが非常に小さいことに注目です。p_2dとq_2dに実際に2次元配列分のメモリが確保されているわけではないと考えられます。また、np.meshgridの場合と比べて、計算時間がかかっていることもこれが原因と考えられます。np.tileでは2次元配列分のメモリが確保されておらず、元の配列のメモリをいちいち参照しに行くと考えられます。元の配列のメモリを参照するだけで良いので、メモリ消費量は少なくすみますが、メモリ参照に時間がかかるため、np.meshgridの場合よりも余計に時間がかかっていると推測されます。
以下を実行してメモリ消費量を確かめます。
# np.tile
_ = get_diff_tile(p,q,verb=True)結果は
- get_diff_tile - size of p_2d: 0.000128 MB size of q_2d: 0.000128 MB size of d_2d: 3.2e+03 MB time for get_diff_tile: 1.710393 sec
となります。
Result | 3手法の計算速度の測定結果まとめ
最後に3つの方法での計算時間のまとめと今回書いたJupyter Notebookの例を掲載します。
計算時間のまとめ | np.ufunc.outerが高速
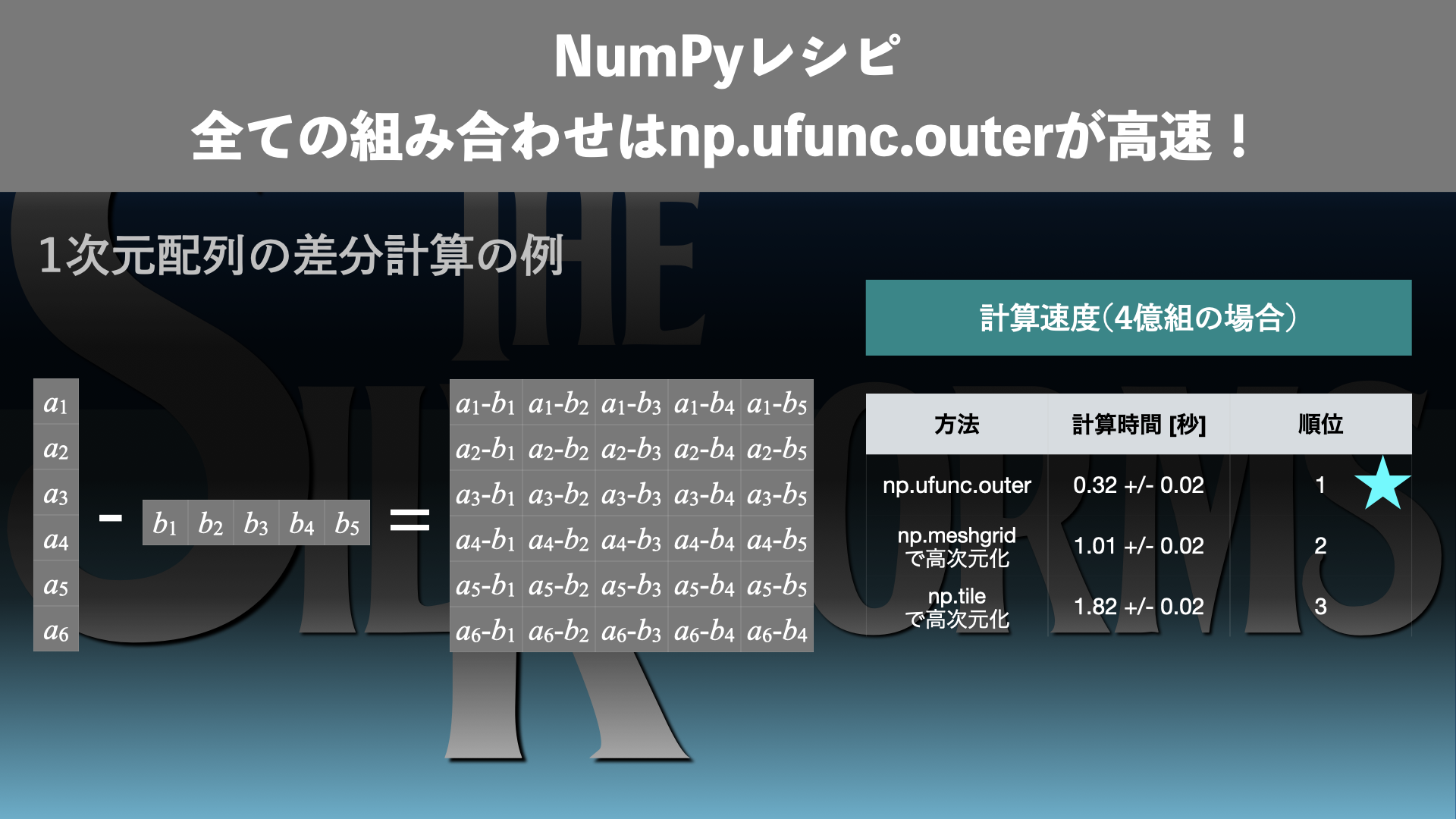
2つの1次元配列について、要素同士の全ての組み合わせの差分を取る計算の時間は以下のようになりました。
| # | 方法 | 計算速度 [秒] | 順位 |
| 1 | np.ufunc.outerで計算 | 0.32 \(\pm\) 0.02 | 1 |
| 2 | np.meshgridで高次元化 | 1.02 \(\pm\) 0.02 | 2 |
| 3 | np.tileで高次元化 | 1.82 \(\pm\) 0.02 | 3 |
この結果から1番目のnp.ufunc.outerで計算する方法が一番高速であることがわかります。2番目の方法よりも3倍、3番目の方法よりも6倍高速であることがわかりました。
今回作成したPythonコードのサンプル
今回書いたPythonコードを載せます。参考にしてください。
Conclusion | まとめ
最後までご覧頂きありがとうございます!
Pythonで、2つの配列の要素同士の全ての組み合わせについての計算を行う際、高速に計算する方法を3つご紹介しました!
- np.ufunc.outerを使う方法
- np.meshgridで高次元化する方法
- np.tileで高次元化する方法
があり、np.ufunc.outerを使う方法が最も高速であることがわかりました。np.ufunc.outerはufuncの部分をadd、subtract、multiply等、NumPyのufuncとして定義された関数にすることで、四則演算や様々な数学計算を要素同士の全ての組み合わせについて行うことができる便利な方法です。
以上「NumPyレシピ | 要素同士の全ての組み合わせについての計算はnp.ufunc.outerが便利!」でした!
またお会いしましょう!Ciao!

コメント