みなさんこんにちは!このブログでは主に
の4つのトピックについて発信しています。
今回の記事では時系列データの分析について扱います!
時系列データを分析するとき、まず確認すべきなのが「そのデータが定常かどうか」です。
もし非定常なデータをそのまま扱ってしまうと、まったく無関係な変数同士でも強い相関があるように見える“偽物の相関”が出てしまいます。前回の記事↗では、ランダムウォークを用いたシミュレーションで、この偽相関が76%の確率で発生することを実証しました。
では、どうすれば事前にデータの性質を見極められるのでしょうか?
その答えの一つが 「定常性の確認」 です。本記事では、ランダムウォークを例に取りながら、定常性とは何かを整理し、さらに ADF(Augmented Dickey-Fuller)検定 を使ってPythonで実際に確認する方法を紹介します。
この記事を読むことで、次のことが理解できます。
- 定常性と非定常性の違いを理解できる
- ランダムウォークが非定常データの代表例である理由を把握できる
- ADF検定を用いた定常性の確認手順を実践できる
時系列データ分析の落とし穴を避けるための「最初の一歩」として、ぜひ最後までご覧ください。
Abstract | ADF検定で定常性を確認すべし
時系列データの分析では、データが定常であること が前提条件になります。
しかし、非定常なデータをそのまま扱うと、無関係な変数同士でも強い相関が観測される「偽物の相関」が生じるリスクがあります。
本記事では、ランダム変数(ホワイトノイズ)とランダムウォークを例に、Pythonで ADF(Augmented Dickey-Fuller)検定を実行します。結果、ランダム変数は定常と判定され、ランダムウォークは非定常と判定されることが確認されました。
この記事を読めば、時系列データ分析において定常性の確認が不可欠であることを理解し、Pythonを使って実務データの定常性を検証する手順を学ぶことができます!
Introduction | 定常性とは?
時系列データの分析を行う際に重要な概念のひとつが 定常性(Stationarity) です。
定常とは「時間が経ってもデータの統計的性質が変わらないこと」を意味します。
定常データの直感的なイメージ
たとえば、サイコロを何度も振ったときの出目や、平均0の正規分布に従う乱数は、時間が経っても分布の形は変わりません。
このように 平均や分散が一定で、時間の経過に依存しない データは「定常」と呼ばれます。
一方で、コインを投げ続けた累積和(いわゆるランダムウォーク)のように、時間が経つほど値が大きく上下にズレていくデータは「非定常」です。
弱定常性の定義
より形式的には、弱定常性(weak stationarity)は次の3条件で定義されます。
- 平均が時間に依存しない(一定である)
- 分散が時間に依存しない(一定である)
- 自己共分散が「時間の差」(ラグ)だけで決まり、絶対的な時間には依存しない
この条件を満たすと「定常データ」と呼ぶことができます。
ホワイトノイズとランダムウォークの例
ホワイトノイズとランダムウォークはそれぞれ、定常データと非定常データの典型例です。
ホワイトノイズ(平均0の正規分布に従う乱数)
→ 平均も分散も一定で、典型的な定常データ。
ランダムウォーク(乱数の累積和)
→ 平均や分散が時間とともに変化する、非定常データの代表例。
図で比較 | 定常過程 vs 非定常過程
実際に「定常なデータ」と「非定常なデータ」を比べてみましょう。
下の図1は、上段がホワイトノイズ(定常)、下段がランダムウォーク(非定常)をプロットしたものです。
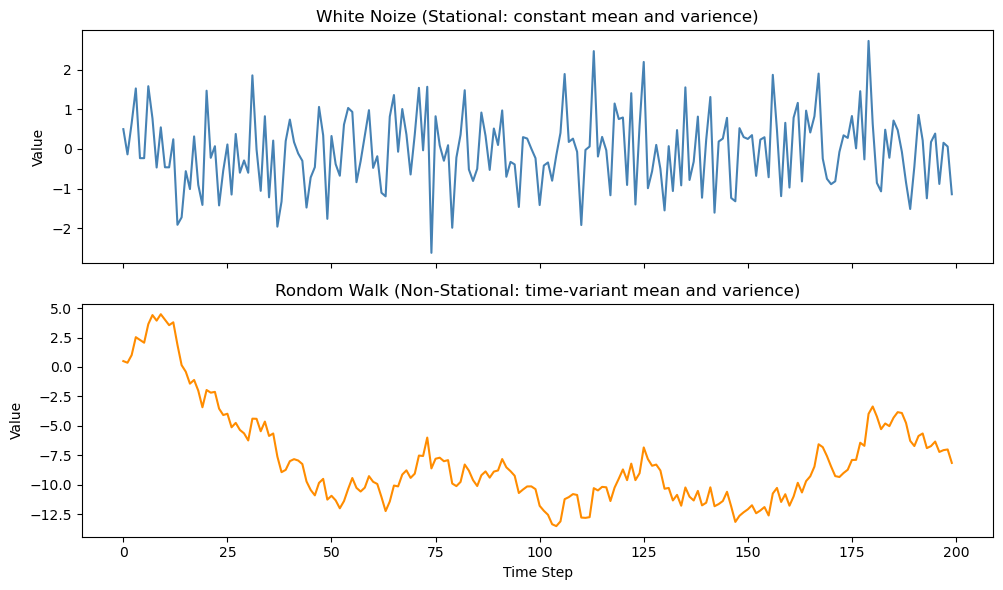
ホワイトノイズは平均0のまわりでランダムに揺れ動くだけで、時間が経っても平均や分散といった分布の形は変わりません。
一方、ランダムウォークは累積的に偏りが蓄積し、時間が経つほど平均や分散が変化していきます。
この違いからわかるように、ランダムウォークは非定常データの典型例です。
非定常データをそのまま相関分析や回帰分析にかけると、統計的な前提が崩れて「偽物の相関」が出やすくなります。
定常性のまとめ
相関分析や回帰分析は、データが「定常」であることを前提にしています。
もし非定常なデータにそのまま適用してしまうと、前回の記事↗で見たように「偽物の相関」が高い確率で観測されてしまいます。
このため、まずはデータの定常性を確認することが欠かせないのです。
Method | 定常性を確認する方法
時系列データが定常かどうかを確認する方法には、大きく分けて 視覚的に確認する方法 と 統計的に確認する方法 があります。
視覚的に確認する
まずはシンプルに、時系列をプロットして眺める方法 です。
- 定常なデータの場合:
平均や分散が時間に依存せず、横ばいに推移します。 - 非定常なデータの場合:
平均が時間とともに変化したり、値の振れ幅(分散)が広がっていったりします。
例えば、先ほど図1↗で示したホワイトノイズ(定常)は時間が経っても分布の性質が変わらない一方、ランダムウォーク(非定常)は時間が経つほど平均や分散が変化してしまいます。このように、時系列のプロットを確認することで、ランダムウォークが時間とともに分布が大きく変化する「非定常」データであることが一目でわかります。
ただし、この方法はあくまで直感的な判断にすぎません。より確実に判定するには、統計的な検定を用いる必要があります。
統計的に確認する(ADF検定)
定常性を統計的に確認する代表的な方法が ADF(Augmented Dickey-Fuller)検定 です。
ADF検定では、以下のように帰無仮説と対立仮説を設定します:
- 帰無仮説(H0):単位根が存在する(=データは非定常)
- 対立仮説(H1):単位根が存在しない(=データは定常)
つまり、ADF検定で得られた p値が小さい(例: 0.05未満) 場合には、帰無仮説を棄却して「このデータは定常である」と結論づけます。逆に、p値が大きければ「このデータは非定常である」と判断されます。
なお、ADF検定には以下の3つのバリエーションがあります:
- 定数のみ(定数周りの定常性を確認)
- 定数+トレンド(トレンド周りの定常性を確認)
- 定数+トレンド+時間項(時間項を含む定常性を確認)
本記事では、前回の「偽物の相関(ランダムウォークの場合)」の検証↗に対応するために、定数周りの定常性 に限定して扱います。
Result | PythonでADF検定を実行してみる
ここからは、実際にPythonを使って ADF検定 を実行し、定常性を確認してみましょう。
比較するのは、以下の2つです。
- ランダム変数(定常データ)
- ランダムウォーク(非定常データ)
ランダム変数(定常データ)の例
まずは、平均0・分散1の正規分布に従うランダム変数(ホワイトノイズ)を生成します。
のデータは時間が経っても分布の性質が変わらないため、定常と判定されるはずです。
import numpy as np
from statsmodels.tsa.stattools import adfuller
# サンプル数
n = 200
np.random.seed(42)
# ランダム変数(ホワイトノイズ)
data_random = np.random.normal(0, 1, n)
# ADF検定
result = adfuller(data_random)
print('ADF:', result[0])
print('p-value:', result[1])出力例(実行環境によって異なります):
ADF: -14.744199946601888
p-value: 2.543125112212854e-27p値が 0.05未満 となっているため、帰無仮説(非定常)を棄却し、「このデータは定常である」と判断できます。
ランダムウォーク(非定常データ)の例
次に、ランダム変数を累積和して ランダムウォーク を生成します。
ランダムウォークは平均や分散が時間とともに変化するため、典型的な非定常データです。
# ランダムウォーク(非定常データ)
rw = np.cumsum(np.random.normal(0, 1, n))
# ADF検定
result = adfuller(rw)
print('ADF:', result[0])
print('p-value:', result[1])出力例:
ADF: -2.3072851790645266
p-value: 0.16962912078943676p値が 0.05以上 となっているため、帰無仮説(非定常)を棄却できません。
つまり、「このデータは非定常である」と判断されます。
結果の比較
以上の結果をまとめると次のようになります。
| データ | 例 | ADF p値 | 判定 |
|---|---|---|---|
| ランダム変数 | 正規分布に従う乱数 | < 0.05 | 定常 |
| ランダムウォーク | 累積和された乱数 | > 0.05 | 非定常 |
このように、ADF検定を用いることで、統計的に「定常か非定常か」を判断できる ことが確認できました。
前回の記事↗で示した「ランダムウォークは偽物の相関を生みやすい」という結果も、統計的に裏付けられたことになります。
Discussion | 実務への示唆
今回の検証からわかるように、非定常なデータをそのまま相関分析や回帰分析に用いると、誤った結論に至る危険性があります。
ランダムウォークはまったく無関係なデータ同士であっても見かけ上は強い相関が観測されてしまうのは、その典型例です。
実務データに多い非定常性
実務で扱う時系列データ(株価、為替、売上、アクセス数など)の多くは、以下のような性質を持ちます:
- トレンドが存在する(長期的に増加・減少する)
- 季節性や周期性がある(月ごと・年ごとに繰り返すパターン)
- ボラティリティが変化する(金融データに多い)
これらはすべて非定常性の要因です。これらの要因により、通常の相関分析の前提が崩れ、偽物の相関や誤った回帰結果につながりやすくなります。したがって、時系列分析の最初のステップとして 必ず定常性を確認する ことが求められます。
定常性確認と前処理の重要性
こうした問題を避けるために、定常性を確認することが第一歩 です。
今回扱ったADF検定は、そのための有効なツールです。p値の大小によって、データが定常か非定常かを統計的に判定できます。
さらに、もし非定常と判定された場合には、次のような前処理を行うのが一般的です。
- 差分を取る(一次差分・対数差分など)
- トレンドを除去する(回帰トレンドを引く)
- 季節調整を行う(移動平均や分解法を用いる)
このような前処理によって、非定常データを定常系列に変換してから分析を行うことで、誤った結論を避けることができます。
👉 まとめると:
- 非定常データをそのまま扱うと偽相関が出る
- ADF検定を使えば定常性を確認できる
- 実務のデータは非定常であることが多いので、前処理が必須
Conclusion | まとめ
本記事では、時系列データにおける定常性の重要性を解説し、Pythonで実際にADF検定を実行することで「定常」と「非定常」の違いを確認しました。
- ランダム変数(ホワイトノイズ)は 定常 と判定された
- ランダムウォークは 非定常 と判定された
- ADF検定によって統計的に「定常か非定常か」を判断できることが確認できた
この結果からわかるように、非定常データをそのまま扱うと偽相関を導くリスクが高いため、時系列データを分析する際には、定常性を確認すべきであることが改めて明らかになりました。
今回扱ったのは「定数周りの定常性」に限定したケースでした。しかし、実際のデータ(株価、GDP、季節性を持つ時系列など)は トレンド や 時間項 を含む場合が多く、より複雑です。
👉 次回の記事では、今回触れた「定常性の拡張」として、トレンドや時間項を含むデータ に対してどのように定常性を検証できるのかを解説します。
株価やGDP、季節性を持つデータを題材に、さらに一歩踏み込んで検証していきましょう。
時系列データ分析を正しく進めるための基礎を、一歩ずつ固めていきましょう!
References | Pythonコードの全文
今回の記事で書いたPythonコード(Jupyter Notebook)の全文は以下です。ご参考にどうぞ!
時系列分析シリーズ
- 偽物の相関(76%)を実証!ランダムウォークに潜む落とし穴
- (今回)ADF検定で定常性を確認すべし
- (次回)トレンドや時間項を含む場合の定常性
- (次々回)非定常データの対処法(差分・トレンド除去・季節調整・ARIMA)
👉 次回は「トレンドや時間項を含む場合の定常性」について解説します!
株価やGDP、季節性を持つ時系列データを題材に、より実務的なケースを検証しますのでお楽しみに。


コメント