みなさんこんにちは!このブログでは主に
の4つのトピックについて発信しています。
今回は時系列データを使った回帰分析の思わぬ落とし穴を紹介します!
時系列データを使った回帰分析では、思わぬ落とし穴があります。
一見すると強い相関があるように見えても、それが「本物の関係性」ではなく、ただの偽物の相関である場合があるのです。
特にランダムウォークのような非定常データでは、この問題が顕著に現れます。本記事では、Pythonを使ってランダムウォークのシミュレーションを行い、相関分析でどのように誤判定が起こるのかを実証します。さらに、モンテカルロシミュレーションにより、76%の確率で独立なデータ間に有意な相関が出てしまうことを確認します。
この記事を読むことで、
- なぜ時系列データで偽物の相関が起こるのか
- 実際にPythonでどのように検証できるのか
- データ分析を正しく進めるために注意すべきポイント
を理解できるはずです。
「時系列データをそのまま相関分析して大丈夫?」と感じたことがある方は、ぜひ最後まで読んでみてください。

この記事はこんな人のお悩み解決に役立ちます!
- 回帰分析などのデータ分析をしている
- 時系列データを扱っている
Abstract | ランダムウォークでは76%の確率で偽物の相関が出る
時系列データをそのまま回帰分析に用いると、独立したデータ同士であっても「偽物の相関」が生じることがあります。本記事では、正規分布に従うランダム変数と、その累積和から生成したランダムウォークを比較し、相関分析をシミュレーションします。ランダム変数同士では相関はほとんど見られない一方、ランダムウォーク同士では相関が観測されます。
さらに、本記事ではモンテカルロシミュレーションによって多数のデータセットを検証します。本来独立であるはずのランダムウォーク同士で 76%の確率で有意な相関が検出される ことが確認されます。
この記事を読めば、時系列データ分析において非定常性を考慮せずに回帰や相関を適用することの危険性が明らかになります。
準備 | Pythonで相関分析をシミュレーション
今回もPythonで分析をしていきます。ここからはJupyter Notebookで一緒に作業することを想定し、一つ一つご紹介していきます。実際にはここで用いた関数を通常のPythonソースコードにコピーして使ったり、Pythonのファイルにまとめてimportして使うのが良いでしょう。ここでは簡単のためにJupyter Notebookで紹介します。
Resultの章にJupyter Notebookでの実装例を掲載するので、そちらを参照していただいても構いません。この章では、簡単な解説とともにソースコードを一つずつ提示します。解説が不要な方はResultの章に飛んでいただき、Jupyter Notebookでの実装例を参考にする方が早いでしょう。
Jupyter Notebookの用意
まずはJupyter Notebookのファイルを開きましょう。Jupyter Notebookの使い方については過去記事「python入門講座|pythonを使ってみよう2(Jupyter Notebookを使う方法)[第5回]」もご覧ください!
ライブラリのインポート
まずはライブラリをインポートしておきます。NumPy, Scipy, Matplotlibなどを使います。以下を実行してください。
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
検証1 | ランダム変数とランダムウォークの違い
ランダムウォークの相関分析の例を一つ見てみましょう。
- 正規分布に従う2つの独立なデータ(ランダム変数)
- 上記データをそれぞれ累計した独立なランダムウォーク
という2パターンについて相関分析を行い、ランダム変数とランダムウォークの違いを検証していきます。
通常のランダム変数の場合の相関分析
まずは正規分布に従うデータを2つ作成します。以下のコードを実行しましょう。
# fix the seed
np.random.seed(1)
# sample size
n_smp = 100
# get independent random variable
t1 = np.random.normal(size=n_smp)
t2 = np.random.normal(size=n_smp)これで変数t1とt2それぞれに、正規分布に従う100個のランダム変数が格納されました。t1とt2は独立なデータとなっています。
ランダム変数同士を時系列でプロット
ランダム変数同士を時系列としてプロットしてみましょう。以下を実行してください。
# time-series plot
plt.title('Randam Variable')
plt.xlabel('step')
plt.ylabel('value')
plt.plot(t1, '+:', lw=0.5, label='t1')
plt.plot(t2, 'x:', lw=0.5, label='t2')
plt.legend()下記の図1のような図が表示されるはずです。
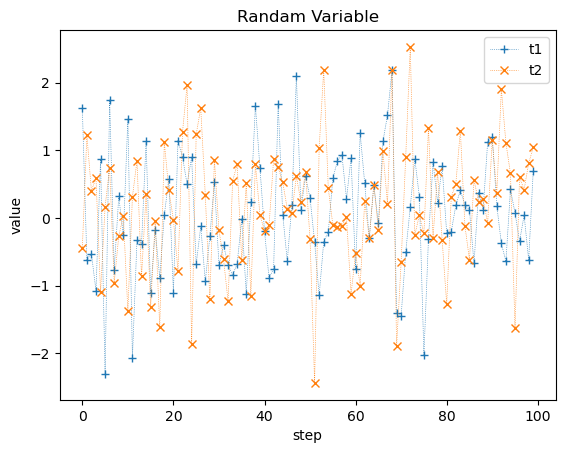
t1とt2はそれぞれ標準正規分布にしたがうので、平均=0を中心に標準偏差=1の範囲に分布していることがわかります。
ランダム変数同士の散布図をプロット
次にランダム変数同士の散布図をプロットしてみましょう。以下を実行してください。
# scatter plot
plt.title('Randam Variable')
plt.xlabel('t1')
plt.ylabel('t2')
plt.plot(t1, t2, '.')実行すると、図2のような図が出力されます。
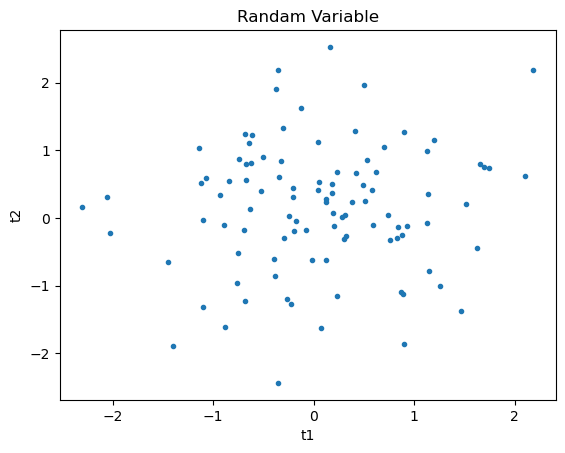
0を中心としてランダムに分布しており、t1とt2の間に相関はないように見えます。
ランダム変数同士の相関係数, 決定係数, p値
ランダム変数t1とt2に相関がないことを確認するため、相関係数・決定係数・p値を計算しましょう。相関係数・決定係数・p値はそれぞれ以下のような意味を持つ数値です。
- 相関係数 \(r\): 変数同士の関係性
- -1から1の値を取り、0から離れるほど強い相関を意味する
- 決定係数 \(r^2\): 変数同士の相関の強さ
- 目的変数の分散のうち、説明変数の変動で説明できる割合
- 0から1の値を取り、1に近いほど強い相関を意味する
- 単回帰の場合は相関係数の2乗となる
- p値 \(p\): ランダムな変数同士からその相関係数が実現する確率
- 小さいほど統計的に有意であることを意味する
- 例えば有意水準5%であれば、\(p\) < 0.05の場合に統計的に有意であると結論づける
以下を実行して、相関係数・決定係数・p値を計算し、表示しましょう。
# get statistics
r, p = sp.stats.pearsonr(t1,t2)
print('r:', r)
print('r2:', r**2)
print('p:', p)実行すると以下のような値となります。
r: 0.0906313197643404 r2: 0.008214036122226119 p: 0.36984380127275324
相関係数\(r\)や決定係数\(r^2\)は0に近く相関はほとんどないと言えます。また、p値も0.37と大きく相関がないことを否定しない結果です。
ランダム変数同士の相関のまとめ
以上のように、独立なランダム変数を生成したうえで相関分析を行うと、当然、相関は見られないという結果になります。
ランダムウォークの場合の相関分析
次にランダムウォークの場合の相関分析を行います。独立な2つのランダム変数t1, t2からランダムウォークx1, x2を生成します。ランダムウォーク\(x_{i}\)はランダム変数\(t_{i}\)から以下のように生成できます。
$$
x_{i+1} = x_{i} + t_{i}
$$
すなわち、ランダム変数t1, t2についてそれぞれ累積和を取ることで、独立な2つのランダムウォークを生成することができます。
Jupyter Notebookで分析を続けます。以下のコードを実行してください。
# then get random walk by cumulative sum
x1 = np.cumsum(t1) # random walk 1
x2 = np.cumsum(t2) # random walk 1これで変数x1, x2にランダムウォークのデータが格納されます。
ランダムウォーク同士を時系列でプロット
時系列でランダムウォークをプロットしてみましょう。以下を実行してみましょう。
# time-series plot
plt.title('Randam Walk')
plt.xlabel('step')
plt.ylabel('value')
plt.plot(x1, label='x1')
plt.plot(x2, label='x2')
plt.legend()実行すると、以下の図3が表示されます。
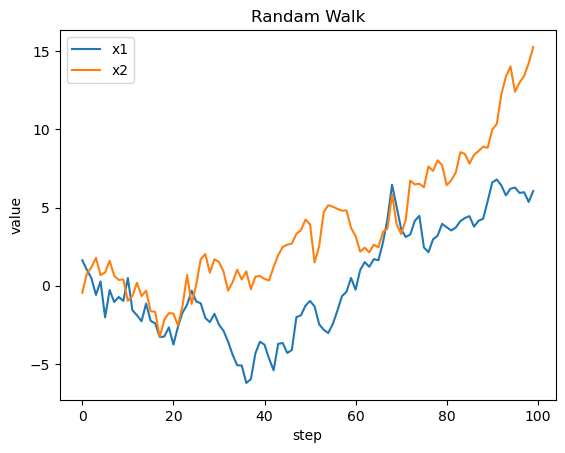
x1とx2は独立なランダムウォークであるにもかかわらず、大局的にはどちらも少し下がって大きく上昇するという似たような動きをしているように見えます。
ランダムウォーク同士の散布図をプロット
次に散布図をプロットしてみましょう。以下を実行してください。
# scatter plot
plt.title('Randam Walk')
plt.xlabel('x1')
plt.ylabel('x2')
plt.plot(x1, x2, '.')実行すると、以下の図4が表示されます。
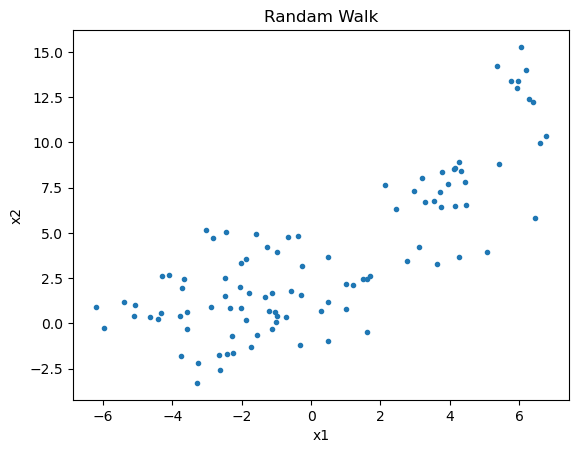
x1とx2は独立なランダムウォークであるにもかかわらず、明らかに正の相関があるように見えます。
ランダムウォーク同士の相関係数, 決定係数, p値
ランダムウォークのx1とx2の相関を確認するために、相関係数・決定係数・p値を計算しましょう。以下を実行してください。
# get statistics
r, p = sp.stats.pearsonr(x1,x2)
print('r:', r)
print('r2:', r**2)
print('p:', p)実行すると以下のような値となります。
r: 0.8014225714888524 r2: 0.6422781380918048 p: 1.326476130542848e-23
相関係数\(r\)は0.8となっており、ランダム変数の場合(0.09)と比べて10倍近い大きな値となっており、強い正の相関があることがわかります。決定係数\(r^2\)も0.64で、ランダム変数の場合(0.008)に比べて100倍近く大きな値となっています。さらに、p値は10の-23乗とほぼゼロです。これは、全く無関係なランダムなデータから、今回のような相関関係が得られる確率がわずは10の-23乗しかないことを意味します。
ランダムウォーク同士の相関のまとめ
このようにランダムウォークの場合、全く無関係で独立なデータであっても、強い相関が観測されることがあります。つまり、ランダムウォークのような時系列データでは偽物の相関が観測されることがあるということです。
考察 | 偽相関の原因は「非定常性」
偽物の相関が現れる原因として、データの非定常性があります。データの定常性については次回以降詳しく扱いますので、ここでは簡単に説明するにとどめます。
定常なデータ: 平均と分散が時間によって変化しない
まずデータが定常であるとは、平均や分散が時間に依存して変化しないことを意味します。
- 定常なデータ
- 平均が一定
- 分散が一定
図1のランダム変数の時系列プロットを見てください。このデータでは、平均と分散が一定で時間によって変化しません。横軸の時系列のどこを切り取っても平均は0、分散は1となっていることがわかります。
非定常なデータ: 平均や分散が時間によって変化する
非定常なデータの場合、平均や分散が時間に依存して変化します。
- 非定常なデータ
- 平均が変化する
- (and/or) 分散が変化する
図3のランダムウォークの時系列プロットを見てください。ランダムウォークは日本語では「酔歩」と言います。つまりふらふらとあっちへ行ったりこっちへ行ったりしており、平均が時間ごとに変化します。ランダムウォークは典型的な非定常データです。
図3の各データの平均を時間step(横軸)ごとに見てみましょう。x1(青線)に着目すると、
- 時間step 0-10程度: 平均は0付近
- 時間step 40程度: 平均は-5付近
- 時間step 100程度: 平均は+5付近
と、時間ごとに平均が変化していることがわかります。x2(オレンジ線)も同様に平均が時間ごとに変化します。
定常性は通常の相関分析の前提
通常の相関分析はデータの定常性(=平均や分散が時間に依存して変化しないこと)を前提としているため、ランダムウォークのような非定常なデータに適用すると正しい結果を得ることができません。非定常なデータに通常の相関分析を適用すると高い確率で偽物の相関が観測されることになります。
検証2 | モンテカルロシミュレーションで確率を確認
本記事後半では、ランダムウォークの場合にどのくらいの確率で偽物の相関が観測されるのか、モンテカルロシミュレーションによって検証していきます。モンテカルロシミュレーションとは、データセットをたくさん生成することで、分布や割合などの統計的な情報を得る手法です。今回は、検証1で生成したランダム変数のデータセットx1, x2やランダムウォークのデータセットt1, t2のようなデータセットをランダムに1000個生成して検証していきます。
モンテカルロシミュレーションを実行する関数
まずはモンテカルロシミュレーションを実行する関数を定義します。検証1をn_sim回実行し、p値と決定係数\(R^2\)の配列ary_p, ary_r2を返す関数です。以下を実行してください。
# function to get Monte-Carlo simulation
def get_MC_sim(n_sim=1000, n_smp=1000, seed=None):
# seed
np.random.seed(seed)
# get output array
ary_r2 = np.zeros([2, n_sim]) # [t,x]
ary_p = np.zeros([2, n_sim]) # [t,x]
# loop
for i in range(n_sim):
# get random
t1 = np.random.normal(size=n_smp)
t2 = np.random.normal(size=n_smp)
# get pearson
r, p = sp.stats.pearsonr(t1, t2)
ary_r2[0,i] = r**2
ary_p[0,i] = p
# get random walk
x1 = np.cumsum(t1)
x2 = np.cumsum(t2)
# get pearson
r, p = sp.stats.pearsonr(x1, x2)
ary_r2[1,i] = r**2
ary_p[1,i] = p
# end
return ary_r2, ary_p上記の関数では、検証1の内容をループ処理で何度も実施しているだけです。以下ではこの関数を使ってモンテカルロシミュレーションを実行していきます。
モンテカルロシミュレーションの実行
先ほど定義した関数を使ってモンテカルロシミュレーションを実行します。決定係数とp値をサンプリングします。以下を実行してください。
# get MC result
ary_r2, ary_p = get_MC_sim(n_smp=n_smp)これでary_r2にランダム変数とランダムウォークの場合の決定係数が、ary_pにp値が格納されました。
決定係数が大きくなる確率とp値が小さくなる確率
独立なランダムウォークの場合に、どの程度の確率で相関ありと判断され得るかを確認してみます。決定係数が大きくなる確率とp値が小さくなる確率を計算しましょう。例えば、決定係数が0.5以上(分散の半分以上が相関関係に起因する。相関係数0.7以上または-0.7以下)とp値0.05以下を判断基準としてみます。以下を実行してください。
# threshold for R2 and p
crit_r2 = 0.5
crit_p = 0.05
# get fraction
frac_r2 = [
len(np.where(ary_r2[0] > crit_r2)[0]) / len(ary_r2[0]),
len(np.where(ary_r2[1] > crit_r2)[0]) / len(ary_r2[1])
]
frac_p = [
len(np.where(ary_p[0] < crit_p)[0]) / len(ary_r2[0]),
len(np.where(ary_p[1] < crit_p)[0]) / len(ary_r2[1])
]
print('R2:', frac_r2)
print('p:', frac_p)実行すると以下のようになります。
R2: [0.0, 0.157] p: [0.049, 0.764]
表にまとめると下記のようになります。
| ランダム変数 | ランダムウォーク | |
| 決定係数 \(R^{2}\) > 0.5 | 0 % | 16 % |
| p値 \(p < 0.05\) | 5 % | 76 % |
ランダム変数の場合には、決定係数が0.5を上回ることはありません。p値が0.05を下回る確率は定義通り5%です。一方で、ランダムウォークの場合には決定係数が0.5を上回る割合が16 %もあり、p値が0.05を下回る割合は76 %にも達します。つまり、ランダムウォーク同士に対して相関分析を行ってしまうと、有意水準を5%に設定したにも関わらず、76 %の確率で有意な相関が検出されてしまいます。
決定係数とp値の分布をプロット
ランダム変数とランダムウォークについて、決定係数の分布とp値の分布をそれぞれプロットしてみましょう。以下を実行してください。
fig = plt.figure(figsize=[12,5])
gs = fig.add_gridspec(1,2)
axs = [plt.subplot(gs[0]), plt.subplot(gs[1])]
fig.suptitle('Random v.s. Random Walk')
# R2
i = 0
axs[i].set_xlabel('$R^{2}$')
axs[i].set_ylabel('$N$')
axs[i].hist(
[ary_r2[0], ary_r2[1]],
bins = np.linspace(0,1,21),
label=['Random Variable', 'Random Walk']
)
axs[i].legend()
axs[i].annotate(
'', #'$R^{2} > %.1f$: %.1f %%' % (crit_r2, frac_r2[1]),
xytext=(crit_r2, 100),
xy=(1.0, 100),
arrowprops=dict(facecolor='grey', shrink=0.0),
)
axs[i].text(
crit_r2, 110,
'$R^{2} > %.1f$: %.0f %%' % (crit_r2, frac_r2[1]*100),
va='bottom',
ha='left',
fontsize=14
)
# p
i = 1
axs[i].set_xlabel('$p$')
axs[i].set_ylabel('$N$')
axs[i].hist(
[ary_p[0], ary_p[1]],
bins = np.linspace(0,1,21),
label=['Random Variable', 'Random Walk']
)
axs[i].legend()
axs[i].annotate(
'', #'$R^{2} > %.1f$: %.1f %%' % (crit_r2, frac_r2[1]),
xytext=(crit_p+0.15, 600),
xy=(0.06, 600),
arrowprops=dict(facecolor='grey', shrink=0.0),
)
axs[i].text(
crit_p+0.16, 600,
'$p < %.2f$: %.0f %%' % (crit_p, frac_p[1]*100),
va='center',
ha='left',
fontsize=14
)実行すると、下記の図5のような図が表示されます。
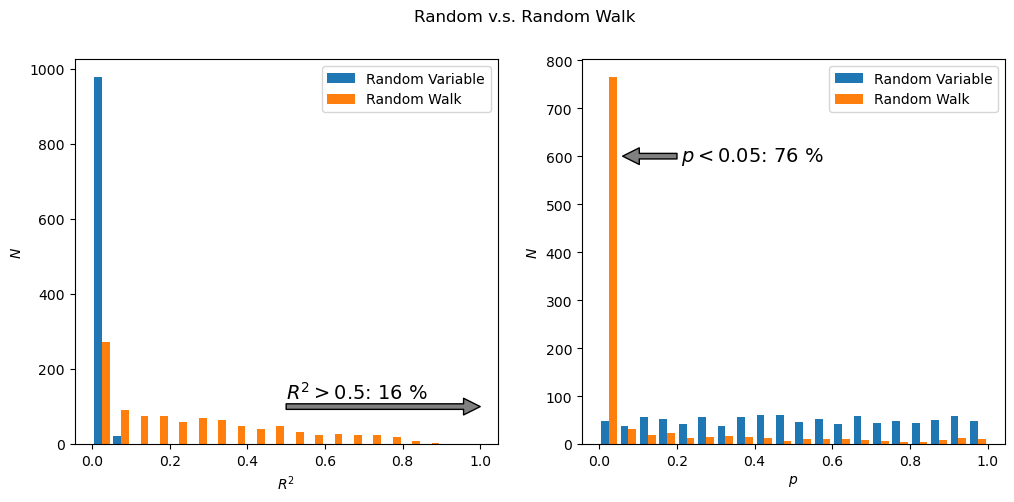
このように、ランダムウォーク同士を相関分析した場合、無関係なデータにも関わらず、
- 高い確率で統計的に有意と判定される(例: p値 < 0.05となる確率が76 %)
- 高い確率で強い相関を持つと判定される(例: \(R^2\) > 0.5となる確率が16 %)
という問題があります。ランダムウォークのような定常性を持たないデータセットを相関分析にかけた場合、本来は全く無関係な独立したデータであるにも関わらず、偽物の相関が高い確率で検出されます。時系列データの相関分析を行うときには、このような偽物の相関に注意する必要があります。
対策 | 偽の相関を避けるために
今回のシミュレーション結果から分かるように、非定常な時系列データをそのまま回帰分析や相関分析に使うのは非常に危険です。独立したデータ同士であっても、有意な相関があるように見えてしまい、誤った結論を導く可能性が高まります。
こうした問題を避けるためには、以下のステップが重要です。
- 定常性の確認
データが平均・分散・自己共分散のいずれも時間に依存しない性質(定常性)を持つかどうかをチェックする必要があります。 - 単位根検定の実施
代表的な方法に ADF(Augmented Dickey-Fuller)検定 や KPSS検定 があります。これらを用いてデータが非定常であるかどうかを統計的に判定します。 - 差分を取る・変換する
非定常と判定された場合には、一次差分や対数差分などを取って定常系列に変換してから分析を行うのが一般的です。 - モデル選択の工夫
相関分析や単純な回帰に頼らず、時系列モデル(ARIMA, VAR など) を適用することで、非定常性や系列間の動的関係を適切に扱えるようになります。
本記事では「偽物の相関がいかに高い確率で出てしまうか」を実証しましたが、次回以降の記事では、定常性の検定と対処法について詳しく解説していきます。
Conclusion | 76%の偽相関から学ぶ教訓
最後までご覧いただきありがとうございます!
本記事では、時系列データの回帰分析に潜む「偽物の相関」のリスクについて解説しました。
- 独立したランダムウォークであっても、強い相関があるように見えてしまう
- その原因は「非定常性」にあり、通常の相関分析では前提が崩れてしまう
- モンテカルロシミュレーションにより、76%もの確率で誤って有意と判定されることが確認された
つまり、時系列データを扱う際には「定常性の確認」が欠かせません。次回以降の記事では、この定常性をどのように確認し、処理すべきかをさらに掘り下げていきます。
データ分析を正しく行うためには、数値の背後にある統計的な前提を意識することが大切です。この記事が皆さまの分析スキル向上に役立てば幸いです!
以上「Pythonで実証!ランダムウォークで76%の偽物相関が出る理由!」でした!
またお会いしましょう!Ciao!
References | Pythonコードの全文
今回の記事で書いたPythonコード(Jupyter Notebook)の全文は以下です。ご参考にどうぞ!
時系列分析シリーズ
- (今回)偽物の相関(76%)を実証!ランダムウォークに潜む落とし穴
- (次回)ADF検定で定常性を確認すべし

コメント