Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
今回は「アラサーOLのためのpython入門講座」シリーズです!この講座では、プログラミング初心者アラサーOLのMi坊さんに、pythonを学習する上でのアドバイスを行います!「パソコンもプログラミングも初心者だけど、プログラミングができるようになりたい!」という方のためにstep-by-stepで解説していきます。
今日は関数入門として関数を使う意義を紹介します。関数とは、よく行う処理をとしてまとめたものです。関数を自分で定義することもできますし、Pythonには「組み込み関数」として様々な関数が用意されています。これらの関数を用いることで、効率的にプログラミングができます!
この記事を読めば、関数をどのように使うと良いか知ることができます。ぜひ最後までお付き合いください!

この記事はこんな人におすすめ
- 初心者だけどpythonを始めた!
- pythonの基本的な使い方を知りたい!
- 独学で学んだpythonの知識を整理したい!
Abstract | 頻出の処理を関数としてまとめてスッキリさせよう
繰り返し登場する処理を関数としてまとめておくことで、シンプルでわかりやすいコードにすることができます。プログラムがある程度複雑になると、複数行に渡るような処理を何回も行う必要がある場面が出てきます。このとき、繰り返し登場する処理をそのままコピー&ペーストで増殖させてしまうと、
- あとで見直したときに、どこで何をしているのかすぐにわからない
- 修正したいときに、あらゆる箇所を直さなくてはならない
など、プログラミングの手間が増えて効率が落ちます。
関数を使って処理をまとめることで、その処理を行いたいときには関数を呼び出す行を1行書けば良くなります。ソースコードがシンプルで短くなるので、どこで何をしているのかわかりやすくなります。また、処理内容を修正したり変更したいときには、関数を定義した箇所を一つだけ変更すれば済みます。このように、関数を使って繰り返し登場する処理をまとめることで、効率よくプログラミングができるようになります。
Background | 同じ処理が何度も登場するとややこしい
プログラミングでは似たような処理を何度も行う場面があります。この処理が1行で書けるような単純なものであれば、特に困りません。しかし、複数行に渡るような少し複雑な処理の場合、プログラミングの中で何度も何度も出てくると、何をやっているのかわかりにくくなるという問題があります。
関数を使わないことで起きる問題を実際に体験してみる
まずは関数を使わずに少し複雑な処理を実際に書いてみて、この問題を体験してみましょう。
例として、正規分布に従うサンプルを作ってプロットする作業を扱います。詳しく理解しなくて構いませんが、サンプルとはここでは数値の集団のことです。正規分布に従うサンプルとは、例えば下図1のオレンジ線のような平均が0、標準偏差が1の正規分布の場合、0付近の数字が最も頻繁に現れ、そこから離れるほど出現頻度が少なくなるような集団です(釣鐘型の分布などと言われます)。下図1の青が「平均が0、標準偏差が1の正規分布に従うサンプル」のヒストグラムで、オレンジの線が正規分布の形です。
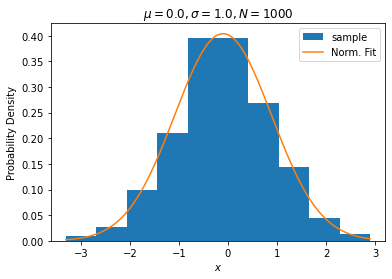
今回の例では、
- サンプル1: μ = 0, σ = 1
- サンプル2: μ = 1, σ = 2
- サンプル3: μ = −3, σ = 4
の3つのサンプルを作って、ヒストグラムを図示するコードを書いてみましょう。ちなみに統計学の世界では平均をμ(ミュー)、標準偏差をσ(シグマ)というギリシャ文字で表すことが多いです。μは平均(真ん中の場所)、σは標準偏差(真ん中からの広がり具合)とおぼえておきましょう。
python notebookの新規作成
まずはpython notebookを用意しましょう。いつものpython_practiceのディレクトリに「practice_func_intro」という名前のpython notebookを作成してください。ターミナルを立ち上げて~/python_practiceに移動、jupyter notebookを起動し、ブラウザから新規→Python3でpython notebookを開いて、ファイル→リネームでファイル名を決定します。
もしやり方がわからなければ、過去記事「python入門講座|pythonを使ってみよう2(Jupyter Notebookを使う方法)」で詳しく解説しているので、これを見ながらやってみてください。
python notebookを起動したら、適宜Markdownセルに説明書きを加えながら下記の説明に沿ってコードを書いて実行していきましょう。Markdownセルやコードセルなどの用語やこれらの使い方についても、過去記事「python入門講座|pythonを使ってみよう2(Jupyter Notebookを使う方法)」を参照してください。練習問題の後にpython notebookの例を掲載します。もし書き方がわからなければそちらを見てください。
ライブラリのインポート
まずは今回必要となるライブラリをインポートします。今回は
- NumPy: 数値計算のためのライブラリ
- matplotlib: 作図のためのライブラリ
- scipy: 科学計算のためのライブラリ
の3つをインポートします。以下を実行してください。
# import
import numpy as np
import matplotlib.pyplot as plt
from scipy import pi
関数を使わない場合のプログラム: ヒストグラムをプロットする例
関数を使わない場合、3つのサンプルを作成してプロットするプログラムがどのようになるか見てみましょう。
サンプル1: μ = 0, σ = 1の正規分布に従うサンプル
まずサンプル1です。下記を実行すると、サンプルを作ってプロットする一連の作業ができます。詳しいことは理解しなくて良いです。行数が多く、少し複雑なプログラムを書く必要があることが理解できればOKです。
# prepare sample
## set parameter: mean, standard deviation, sample size
mu, sigma, N = 0.0, 1.0, 1000
## get sample
data_sample = np.random.normal(loc = mu, scale = sigma, size = N)
# plot the sample
## set figure and axes
fig = plt.figure()
ax = plt.subplot(111)
ax.set_xlabel('$x$')
ax.set_ylabel('Probability Density')
ax.set_title('$\mu = %.1f, \sigma = %.1f, N = %d$' % (mu, sigma, N))
## plot probability density with histogram
ax.hist(data_sample, density = True, label = 'sample')
## plot Normal distribution from the sample
### get parameters
mu_smp = np.mean(data_sample)
sig_smp = np.std(data_sample)
### prepare x and y. y = Norm(x, mu_smp, sig_smp)
x = np.linspace(np.min(data_sample), np.max(data_sample), 1000)
y = np.exp(-0.5 * ((x - mu_smp)/sig_smp)**2) / ((2*pi)**(0.5) * sig_smp)
### plot
ax.plot(x, y, label = 'Norm. Fit')
## set legend
ax.legend()実行すると、下図2のような図が表示されます。

この処理を1回行うだけであれば、コメントも適宜記入していますし、どこで何をやっているか知識があればわかるでしょう。
サンプル2, 3: μ = 1, σ = 2の正規分布に従うサンプルとμ = 3, σ = 4の正規分布に従うサンプル
上記の処理を他の2つサンプルについてもやってみましょう。上記のコードをコピペしてから、
## set parameter: mean, standard deviation, sample size mu, sigma, N = 0.0, 1.0, 1000
の部分を書き換えて、以下を実行してみましょう。
# - Sample2 Norm(1,2) - #
# prepare sample
## set parameter: mean, standard deviation, sample size
mu, sigma, N = 1.0, 2.0, 5000
## get sample
data_sample = np.random.normal(loc = mu, scale = sigma, size = N)
# plot the sample
## set figure and axes
fig = plt.figure()
ax = plt.subplot(111)
ax.set_xlabel('$x$')
ax.set_ylabel('Probability Density')
ax.set_title('$\mu = %.1f, \sigma = %.1f, N = %d$' % (mu, sigma, N))
## plot probability density with histogram
ax.hist(data_sample, density = True, label = 'sample')
## plot Normal distribution from the sample
### get parameters
mu_smp = np.mean(data_sample)
sig_smp = np.std(data_sample)
### prepare x and y. y = Norm(x, mu_smp, sig_smp)
x = np.linspace(np.min(data_sample), np.max(data_sample), 1000)
y = np.exp(-0.5 * ((x - mu_smp)/sig_smp)**2) / ((2*pi)**(0.5) * sig_smp)
### plot
ax.plot(x, y, label = 'Norm. Fit')
## set legend
ax.legend()
# - Sample3 Norm(3,4) - #
# prepare sample
## set parameter: mean, standard deviation, sample size
mu, sigma, N = 3.0, 4.0, 10000
## get sample
data_sample = np.random.normal(loc = mu, scale = sigma, size = N)
# plot the sample
## set figure and axes
fig = plt.figure()
ax = plt.subplot(111)
ax.set_xlabel('$x$')
ax.set_ylabel('Probability Density')
ax.set_title('$\mu = %.1f, \sigma = %.1f, N = %d$' % (mu, sigma, N))
## plot probability density with histogram
ax.hist(data_sample, density = True, label = 'sample')
## plot Normal distribution from the sample
### get parameters
mu_smp = np.mean(data_sample)
sig_smp = np.std(data_sample)
### prepare x and y. y = Norm(x, mu_smp, sig_smp)
x = np.linspace(np.min(data_sample), np.max(data_sample), 1000)
y = np.exp(-0.5 * ((x - mu_smp)/sig_smp)**2) / ((2*pi)**(0.5) * sig_smp)
### plot
ax.plot(x, y, label = 'Norm. Fit')
## set legend
ax.legend()とっても長いコードになりました。上記を実行すると、下図3, 4が表示されます。
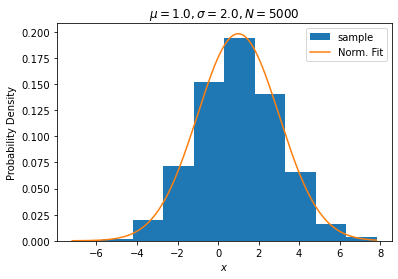
図3. サンプル2のヒストグラム(青)と正規分布の形(オレンジ)。
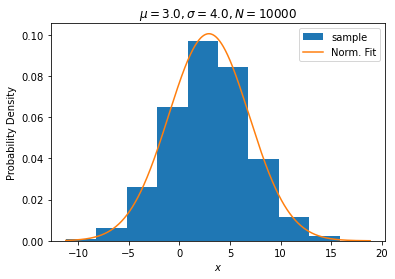
関数を使わずに長いコードを書くことの問題点
プログラムを書くときにはコピー&ペーストして少し編集するだけで済みますが、これだけ長い処理が一つのコードセルに入っていると、スクロールしてコードを見直すのも大変です。また、同じ処理が何度も出てきますが、それが同じ処理なのか前の処理と同じものなのかいちいち判断するのも大変です。あとで見返したときにどこでなにをしているのか把握するのに時間がかかります。
Medthod | 関数として処理をまとめる
繰り返し登場する処理を関数としてまとめておくことでプログラム全体をスッキリさせることができます。
関数を使う場合も実際に体験してみる
関数を使う場合の例を見てみましょう。先程と同じ3つのサンプルをプロットする例です。
関数の準備
まず、ある程度のまとまりで処理をまとめた関数を準備します。どこからどこまでをひとまとまりとするかで、準備する関数は異なってきます。ここでは、
- サンプルを得る関数
- サンプルをプロットする関数
- サンプルから正規分布の形を得る関数
- 正規分布の確率密度を得る関数
- サンプルを得てプロットするまでをひとまとまりにした関数
の5つを準備することにします。
サンプルを得る関数
サンプルを得る関数では下記を入力と出力とします。
- 引数(入力): 平均μ, 標準偏差σ, サンプルサイズN
- 返り値(出力): サンプルのデータ(NumPy配列: data_sample)
この関数を定義しておくことで、「np.random.normal(…)」の長い一文をいちいち書き下さなくて済むようになります。以下を実行しておきましょう(実行しても何も出力されません)。
# get sample following normal distribution
def get_sample_from_normal(mu, sigma, N):
'''
arguments:
mu <float>: mean for Normal distribution
sigma <float>: standard deviation for Normal distribution
N <int>: sample size
returns:
<1d array>: sample from the Normal distribution
'''
return np.random.normal(loc = mu, scale = sigma, size = N)ちなみに冒頭の「”’」で囲まれたコメント部分では、引数(入力)と返り値(出力)の簡単な説明を書いています。
これで「get_sample_from_normal(mu, sigma, N)」というおまじないを書くだけで、正規分布に従うサンプルを得ることができるようになりました。
正規分布の確率密度を得る関数
この関数では、平均μ, 標準偏差σとxが与えられたときに、xにおける正規分布の確率密度関数の値(Probability Density)を返します。引数と返り値は以下です。
- 引数(入力): NumPy配列x, 平均μ, 標準偏差σ
- 返り値(出力): xにおける正規分布(平均μ, 標準偏差σ)の確率密度
この関数を用意しておくことで
$$
\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp\left( – \frac{1}{2} \left(\frac{x-\mu}{\sigma}\right)^{2} \right)
$$
という正規分布の確率密度関数を表す複雑な数式をいちいち書かなくて済みます。
この関数は「サンプルから正規分布の形を得る関数」で使用されるので、それより先に定義しておく必要があります。以下を実行しておきましょう。
# get Normal distribution pdf
def get_normal_pdf(x, mu, sigma):
'''
arguments:
x <array>: x at which probability density is computed
mu <float>: mean for Normal distribution
sigma <float>: standard deviation for Normal distribution
returns:
<array>: Probability density at x
'''
return np.exp(-0.5 * ((x - mu)/sigma)**2) / ((2*pi)**(0.5) * sigma)
サンプルから正規分布の形を得る関数
この関数では、サンプルのデータ(data_sample)が与えられたときに、そのサンプルを表す正規分布の形(x, y)を返します。xはdata_sampleの最小値から最大値までのN個の点、yはそこにおける確率密度です。
- 引数(入力): サンプルのデータ(NumPy配列: data_sample), 点の数N
- 返り値(出力): x, y
以下を実行しておきましょう。
# get Normal distribution pdf from sample
def get_NormalPdf_from_sample(data_sample, N = 10000):
'''
arguments:
data_sample <array> sample from which Normal distribution probability density is computed
N <int>: number of points between min and max of data_sample
returns:
x <1d arrray [N]>: sampling point along x
y <1d arrray [N]>: probability density at x
'''
# get parameters
mu_smp = np.mean(data_sample)
sig_smp = np.std(data_sample)
# prepare x and y. y = Norm(x, mu_smp, sig_smp)
x = np.linspace(np.min(data_sample), np.max(data_sample), N)
y = get_normal_pdf(x, mu_smp, sig_smp)
# end
return x, yこの関数ではまず、サンプルのデータ(data_sample)の平均と標準偏差を求め、mu_smpとsig_smpという変数に格納しています。それから、data_sampleの最小値から最大値までのN個の点として変数xを作成します。そして、先程作成した関数get_normal_pdfを使って変数yを作っています。
サンプルをプロットする関数
サンプルのデータ(data_sample)が与えられたときに、そのサンプルのヒストグラムと正規分布をプロットする関数を準備します。
- 引数(入力): サンプルのデータ(NumPy配列: data_sample), μ, σ, N, N_x
- 返り値(出力): なし
この関数の引数はdata_sampleに加え、data_sampleを作ったときに使った平均μ、標準偏差σ, サンプルサイズN, 正規分布の形の描画に使う点の数N_xです。μ, σ, Nはグラフのタイトルに値を書くためだけに使い、N_xは正規分布の描画だけに使うので必ずしも与える必要はありません。なので、「mu = None」のようにデフォルト値を定義することで、オプション引数としておきます。ここでは詳しく理解する必要はありませんので、そんなものかと思ってください。
以下を実行しておきましょう。
# plot sample with normal distribution
def plot_sample_with_normal(data_sample, mu = None, sigma = None, N = None, N_x = 10000):
'''
arguments:
data_sample <array> sample from which Normal distribution probability density is computed
mu <float>: mean for Normal distribution for data_sample
sigma <float>: standard deviation for Normal distribution for data_sample
N <int>: sample size of for data_sample
N_x <int>: number of points between min and max of data_sample
returns:
None
'''
## set figure and axes
fig = plt.figure()
ax = plt.subplot(111)
ax.set_xlabel('$x$')
ax.set_ylabel('Probability Density')
ax.set_title('$\mu = %.1f, \sigma = %.1f, N = %d$' % (mu, sigma, N))
## plot probability density with histogram
ax.hist(data_sample, density = True, label = 'sample')
## plot Normal distribution from the sample
### prepare x and y. y = Norm(x, mu_smp, sig_smp)
x,y = get_NormalPdf_from_sample(data_sample, N = N_x)
### plot
ax.plot(x, y, label = 'Norm. Fit')
## set legend
ax.legend()詳しい説明はしませんが、「ax.hist(…)」のところでサンプルのヒストグラムを、「ax.plot(…)」で正規分布の形をプロットしています。
サンプルを得てプロットするまでをひとまとまりにした関数
最後に、サンプルのデータ(data_sample)を習得してプロットするまでをひとまとまりにした関数を準備しておきます。作りたいサンプルの平均μ、標準偏差σ、サンプルサイズNを与えるだけで、サンプルの作成からプロットまでできるようにします。引数と返り値は以下です。
- 引数(入力): 平均μ, 標準偏差σ, サンプルサイズN, 正規分布の点数N_x(オプション引数)
- 返り値(出力): なし
以下を実行しておきましょう。
# get sample and plot
def get_plot_sample_from_normal(mu, sigma, N, N_x = 10000):
'''
arguments:
mu <float>: mean for Normal distribution for data_sample
sigma <float>: standard deviation for Normal distribution for data_sample
N <int>: sample size of for data_sample
N_x <int>: number of points between min and max of data_sample
returns:
None
'''
# get sample
data_sample = get_sample_from_normal(mu, sigma, N)
# plot sample
plot_sample_with_normal(data_sample, mu = mu, sigma = sigma, N = N, N_x = N_x)この関数の内容はパット見ただけで「get_sample_from_normal」で正規分布に従うサンプルを作っていて、「plot_sample_with_normal」で図をプロットしていることがわかると思います。一つ一つは複雑なプロセスでも関数でまとめることで、シンプルにわかりやすくすることができます。
サンプルをプロットする処理の実行
関数が準備できたので、サンプルを作ってプロットする処理を実行しましょう。処理自体は一行で完了します。
サンプル1: μ = 0, σ = 1の正規分布に従うサンプル
まずはサンプル1です。以下を実行すれば完了です。
# sample 1
get_plot_sample_from_normal(0.0, 1.0, 1000)関数「get_plot_sample_from_normal」を呼び出すだけです。実行すると、先程の図2と同じ図が出力されます。
サンプル2, 3: μ = 1, σ = 2の正規分布に従うサンプルとμ = 3, σ = 4の正規分布に従うサンプル
残りのサンプルもプロットしてみましょう。以下を実行すれば終わりです。
# sample 2
get_plot_sample_from_normal(1.0, 2.0, 5000)
# sample 3
get_plot_sample_from_normal(3.0, 4.0, 10000)実行すると図3と同じものが出力されます。
Results | コーディング例
上記のコーディングの例を掲載します。参考にしてください。
おつかれさまでした!
今日はここまでです。Python Notebookを終了しておきましょう。もしPython Notebookを終了方法がわからなければ過去記事「python入門講座|pythonを使ってみよう2(Jupyter Notebookを使う方法)」の「Python Notebookの起動・終了方法」の章を参照してください!
Conclusion | まとめ
最後までご覧いただきありがとうございます!
関数を使うことで、繰り返し出現する処理をまとめることができ、コードをシンプルかつわかりやすくするできることを紹介しました。ある程度複雑な処理を行うのに必要な使うテクニックです。次回以降、詳しい方法を解説しますのでお楽しみに!
以上「python入門講座 | 関数の基礎1(関数を使う意義)」でした!
またお会いしましょう!Ciao!
References | 参考
以下の教科書を参考にして進めています!より詳しく学びたい方は購入して読んでみてください!
Pythonの参考教科書
- 現場で使える! Python深層学習入門 Pythonの基本から深層学習の実践手法まで (AI & TECHNOLOGY)
深層学習をpythonで学ぶための教科書ですが、最初の60ページぐらいがpythonの基礎的な解説に割かれています。簡潔にまとまっていてわかりやすいです。
コメント