Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
今回はPythonデータ解析、exp(x)を高速に計算する方法を紹介します。Exponential(exp(x)やeのx乗)の計算は統計学やデータ解析で頻出の計算です。Pythonでは、numpy.expやe**xなど、実装方法がいくつかあるので、いくつかの実装方法について計算速度を比較します。
この記事を読めば、データサイエンスで頻出のexp(x)を高速に計算する方法がわかります。

この記事はこんな人におすすめ
- Pythonでデータ解析をしている
- Numpyでexp(x)を高速に計算したい
Abstract | exp(x)の計算はnp.exp(x)が高速
Pythonでは、一つの計算を様々な方法で実現することができ、計算結果は同じでも計算速度が方法によって異なります。データサイエンスでは、大きな配列xに対して\(\exp(x)\)の計算を行う場面が多くあり、np.exp(x)、e**xなど複数の実装方法が存在します。
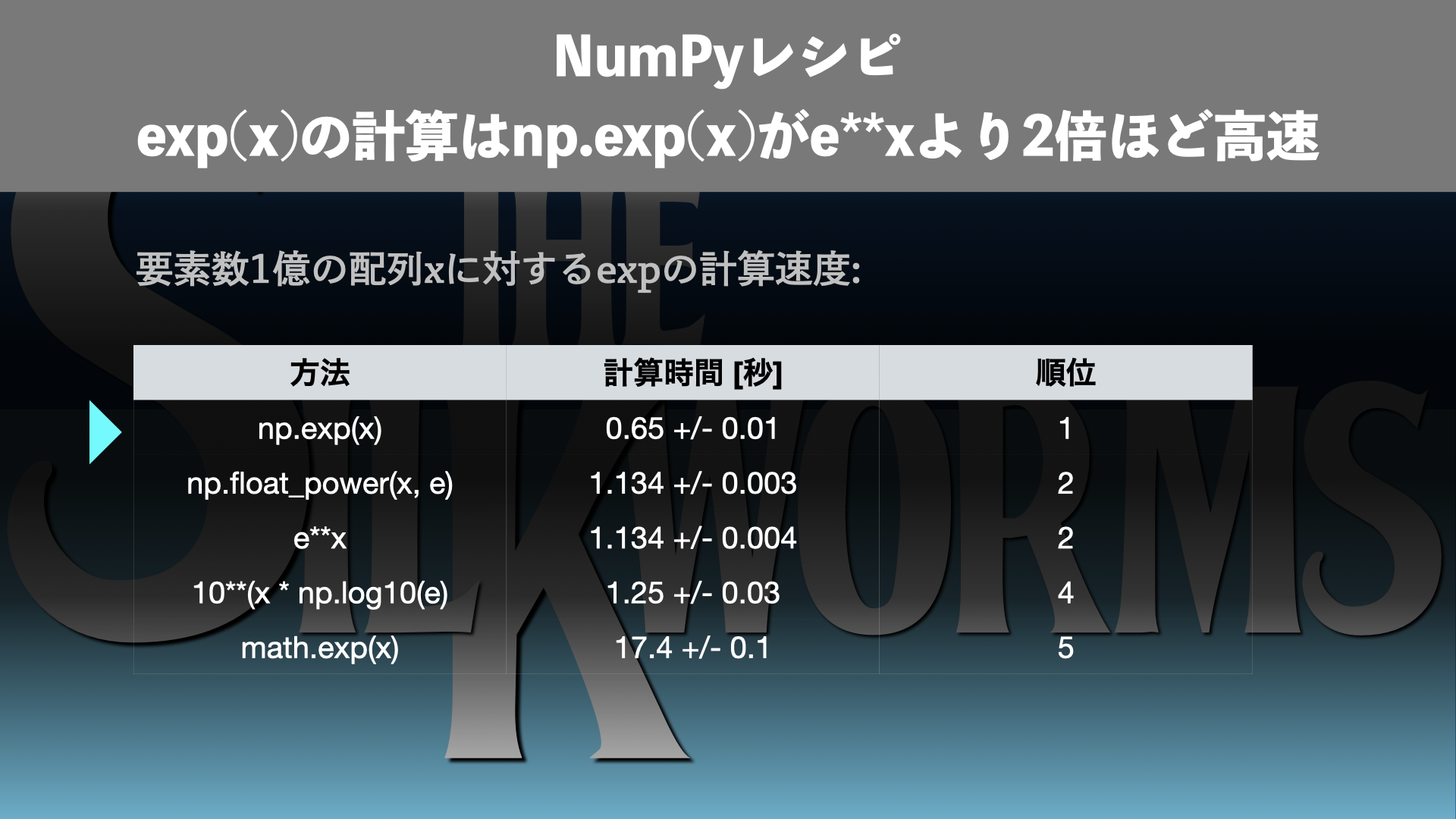
そこで、今回は大きな配列xに対して\(\exp(x)\)の計算を行う場面で、3つ(+おまけ2つ)の実装方法の計算速度を測定しました。結果、np.exp(x)がe**xなどの方法よりも約2倍高速であることがわかりました。
Pythonで\(\exp(x)\)の計算を少しでも高速化したいという方はぜひ最後までご覧ください!
Background | やりたいこと
サイズの大きな配列xについて、各要素のExponentialを計算するということを行います。例えば、10000 x 10000の2次元配列で、要素が合計1億個あるとき、1億個のExponentialをどのように計算すれば高速かを考えていきます。
配列計算のポイント | NumPyに対応した方法を使う
配列計算の高速化でポイントとなるのは、NumPyに対応した方法を使うことです。NumPyに対応した方法であれば、NumPy配列に対してforループなどを使わずに高速計算できます。
NumPy対応のExponentialの計算方法の例
Exponentialの計算であれば、
np.exp(x)np.float_power(e, x)e**x
といった方法はNumPyに対応しています。すなわち、変数xはNumPy配列として定義されていてもそのまま計算できます。
NumPyに対応していないExponentialの計算方法の例
逆に、NumPyに対応していない計算方法も紹介しておきます。例えば、数値の計算と聞いて、mathライブラリの関数
math.exp(x)
の利用を考える方も多いかもしれません。しかし、mathライブラリはNumPyに対応していないので、変数xはNumPy配列ではなくfloat型でなければなりません。したがって、要素数の数だけループを回す必要があります。
Method | exp(x)を計算する3手法で計算速度を測定する
さて、実際にJupyter Notebookでコードを書き、NumPy対応の3手法
np.exp(x)np.float_power(x, e)e**x
を実装し、計算速度を測定していきます。
準備 | ライブラリ、変数x、関数群
まずは準備として、
- 必要なライブラリのインポート
- 配列変数
xの準備 - 計算に用いられる関数群の準備
をしていきます。
ライブラリのインポート
まずは必要なライブラリをインポートします。Jupyter Notebookのコードセルで以下を実行します。
import numpy as np
from scipy import e
import time当然NumPyを使うのでnpとしてインポートしておきます。また、e**xなどで用いるeはSciPyからインポートしておきます。Timeライブラリは計算時間の測定に使います。
配列変数xの作成
サイズの大きな配列xを作っておきます。ここでは[10000, 10000]の2次元配列とし、値は標準正規分布に従うランダムな数値としておきます。以下を実行して変数xを作成しておきます。
# define array: x
x = np.random.normal(0, 1, size=(10000, 10000))
関数群の準備
Exponentialの計算
np.exp(x)np.float_power(x, e)e**x
を実行する関数と時間を測定する関数を用意しておきます。以下を実行します。
# np.exp
def func_np_exp(x):
return np.exp(x)
# np.power
def func_np_float_power(x, e=e):
return np.float_power(e, x)
# e**x
def func_e_pow_x(x, e=e):
return e**x
# measure runtime
def mes_run_time(fnc, *args, n=5):
# time array
t_dat = np.zeros([n])
# loop for n
for i in range(n):
# get start UNIX time
t0 = time.time()
# run process
ret = fnc(*args)
# get end time
t1 = time.time()
# to array
t_dat[i] = (t1-t0)
# - show result - #
print(' results:', ret.ravel()[:3])
# - avg, std - #
t_avg = np.average(t_dat)
t_std = np.std(t_dat)
# - verb - #
print(' delta t [s] = %f +/- %f' % (t_avg, t_std))
# - end - #
return t_avg, t_std関数mes_run_time(fnc, *args, n=5)は時間を測定する関数です。任意の関数fncを任意の引数*argsを与えて実行し、n回測定したときにの平均の計算時間と計算時間の標準偏差を返す関数です。デフォルトでは5回測定して平均と標準偏差を計算し、実行時間を標準出力に表示します。また、fnc(*args)の計算結果の最初の3つも念のため表示します。なお、*argsのようにargsの前に*をつけるのは、複数の引数をfncにわたすことを想定しているためです。
Exponentialを計算するための3つの関数
func_np_exp(x)func_np_float_power(x, e=e)func_e_pow_x(x, e=e)
を定義しておく理由はこの後のコードをシンプルにするためです。すなわち、時間を測定する関数mes_run_time(fnc, args, n=5)のfncにこれら3つの関数を、xに配列xを与えるだけで時間の測定をするためです。np.expだけはこのように独自関数でラップしなくても関数mes_run_time(fnc, args, n=5)に与えることができますが、他の2つnp.float_power(x, e)とe**xについては、このように独自関数でラップし、fnc(args)という形で実行できるようにしておく必要があります。
exp(x)の計算時間の測定
3手法
np.exp(x)np.float_power(x, e)e**x
の計算時間を測定していきます。
np.exp(x)の計算時間 | 0.65 +/- 0.01 秒
まずはnp.exp(x)の場合です。以下を実行します。
# np.exp
_ = mes_run_time(func_np_exp, x)実行結果は
results: [0.83700662 0.88622568 4.62454792] delta t [s] = 0.655137 +/- 0.010341
となりました。0.65 \(\pm\) 0.01秒という結果です。
なお、この結果は実行環境によって変化するのでご留意ください。また、resultsに表示される結果もxによって変化します。配列xがランダムな値なので、xを作成するたびに変化しますが、そうでない限りresultsの表示は変化しないので、他の手法でも同じ値になることを確認できます。
np.float_power(x)の計算時間 | 1.134 +/- 0.003 秒
次にnp.float_power(x)の場合です。以下を実行します。
# np.float_power
_ = mes_run_time(func_np_float_power, x)実行結果は
results: [0.83700662 0.88622568 4.62454792] delta t [s] = 1.134152 +/- 0.002630
となりました。1.134 \(\pm\) 0.003 秒なので、np.exp(x)の倍近い時間がかかることがわかりました。
e**xの計算時間 | 1.134 +/- 0.004 秒
最後にe**xの場合の実行時間を測定します。以下を実行します。
# e**x
_ = mes_run_time(func_e_pow_x, x)結果は
results: [0.83700662 0.88622568 4.62454792] delta t [s] = 1.134401 +/- 0.003872
となりました。1.134 \(\pm\) 0.004 秒なので、np.float_power(x)を使った場合と誤差の範囲で一致しています。こちらもnp.exp(x)の倍近い時間がかかります。
おまけ1: 10**(np.log10(e)*x)の実行時間 | 1.25 +/- 0.03 秒
ここからはおまけです。「e**xよりも10**Xの方が計算速度が速いかもしれない」という仮説のもと、10**Xを使った計算も試してみます。以下の計算から、Xの部分はnp.log10(e)*xとすれば、e**xと10**Xは同値となります。
$$
\begin{align}
y &= e^{x} \\
\ln(y) = \frac{\log(y)}{\log(e)} &= x \\
\log(y) &= x \log(e) \\
y &= 10^{x \log(e)}
\end{align}
$$
ただし、\(\ln\)は\(e\)を底とする自然対数、\(\log\)は10を底とする常用対数。
この計算を実行する関数func_ten_pow_Xを定義し、実行時間を測定します。以下を実行します。
# define function for 10**X
def func_ten_pow_X(x, e=e):
return 10**(np.log10(e)*x)
# measure time
_ = mes_run_time(func_ten_pow_X, x)実行結果は
results: [0.83700662 0.88622568 4.62454792] delta t [s] = 1.251330 +/- 0.029141
です。1.25 \(\pm\) 0.03 秒なので、e**xよりも遅いことがわかりました。
おまけ2: math.exp(x)の実行時間 | 17.4 +/- 0.1 秒
おまけとして、NumPy対応でないmath.expを使う場合も調べてみましょう。前述のとおり、math.exp(x)の引数xにNumPy配列を与えることができないため、配列に対してループを回す必要があります。そのため、上記で紹介した方法に比べてとんでもなく時間がかかります。
これまで同様、実行のための関数を用意して実行時間を測定します。以下を実行してみましょう。
# import math
import math
# define function for math.exp(x)
def func_math_exp(x:np.array):
"""
Args:
x (2d array): 2d numpy array
Returns:
exp(x): 2d numpy array
"""
# prepare output array
y = np.zeros_like(x)
# loop for 2d array
for i1 in range(len(x)):
for i2 in range(len(x[i1])):
y[i1,i2] = math.exp(x[i1,i2])
# end
return y
# measure time
_ = mes_run_time(func_math_exp, x)Mathライブラリが必要なのでここでインポートしています。関数func_math_expの引数xはNumPy配列ですが、ループを回すために2次元配列を前提とします(これまで出てきた関数では、そのような前提は不要だったことからもNumPyの利便性が伺えます)。
実行結果は、
results: [0.83700662 0.88622568 4.62454792] delta t [s] = 17.442881 +/- 0.113327
となります。17.4 \(\pm\) 0.1 秒なので、他の方法よりも遥かに時間がかかっています。配列に対して計算する際に、NumPy対応の関数を使ってループを排除する重要性がわかります。
Result | 3手法の計算速度の測定結果まとめ
サイズの大きな配列xについて\(\exp(x)\)を計算する方法3つ(+おまけ2つ)の計算速度の測定結果をまとめると以下のようになります。
| # | 方法 | 計算速度 [秒] | 順位 |
| 1 | np.exp(x) | 0.65 +/- 0.01 | 1 |
| 2 | np.float_power(e, x) | 1.134 +/- 0.003 | 2 |
| 3 | e**x | 1.134 +/- 0.004 | 2 |
| おまけ1 | 10**X | 1.25 +/- 0.03 | 4 |
| おまけ2 | math.exp(x)+loop | 17.4 +/- 0.1 | 5 |
この結果から、np.exp(x)が一番高速であることがわかります。np.exp(x)ではe**xの半分程度の処理時間で済みます。np.float_power(x)とe**xの実行時間は誤差の範囲で一致しており、内部的には同じ処理が行われていると推測されます。10**Xはe**xよりも遅く、`X = np.log10(e)*x`の計算の分だけ余計に時間がかかると推測されます。math.exp(x)を使うためにループする方法は桁違いに遅く、NumPy対応の計算を行う重要性が理解できます。
今回作成したPythonコードのサンプル
今回書いたPythonコードを載せます。参考にしてください。
Conclusion | まとめ
最後までご覧頂きありがとうございます!
Pythonで、サイズの大きな配列xについて、\(\exp(x)\)を高速に計算するをご紹介しました!
Pythonでは、一つの計算を様々な方法で実装することができます。計算結果は同じでも計算速度は実装方法によって差があり、対象が配列なのか一つの値なのかなど、条件によっても変化します。今回\(\exp(x)\)についてはnp.exp(x)がe**xよりも約2倍高速であることがわかりました!データサイエンスなど統計学の計算や科学計算では\(\exp(x)\)は頻出なので、np.exp(x)を使うことでなるべく高速なコードを書くことができます。
以上「NumPyレシピ | np.exp(x)はe**xよりも2倍ほど高速!」でした!
またお会いしましょう!Ciao!
コメント