みなさんこんにちは!このブログでは主に
の4つのトピックについて発信しています。
今回はPythonデータ解析です!Matplotlib軸のスケールシリーズ第2回として、Matplotlib側で予め用意されている7種類のスケールをご紹介します!Matolitibにはlinear, log, logit, symlog, asinh, function, fuctionlogという7つが用意されており、これらは簡単に設定することができます!
この記事を読めば、作図する際、適切な軸のスケールに簡単に変更する方法を知ることができます!ステップ・バイ・ステップで、サンプルコード付きで解説するので、マネしてコーディングできます!ぜひ最後までご覧ください。

この記事はこんな人のお悩み解決に役立ちます!
- Pythonの作図で軸のスケールを変えたいけどどうやる?
- 負の値も対数スケールでプロットできないの?
- 散布図のデータ点が潰れて見にくいのはどうしたら良い?
Abstract | Matplotlibで予め用意されたスケール
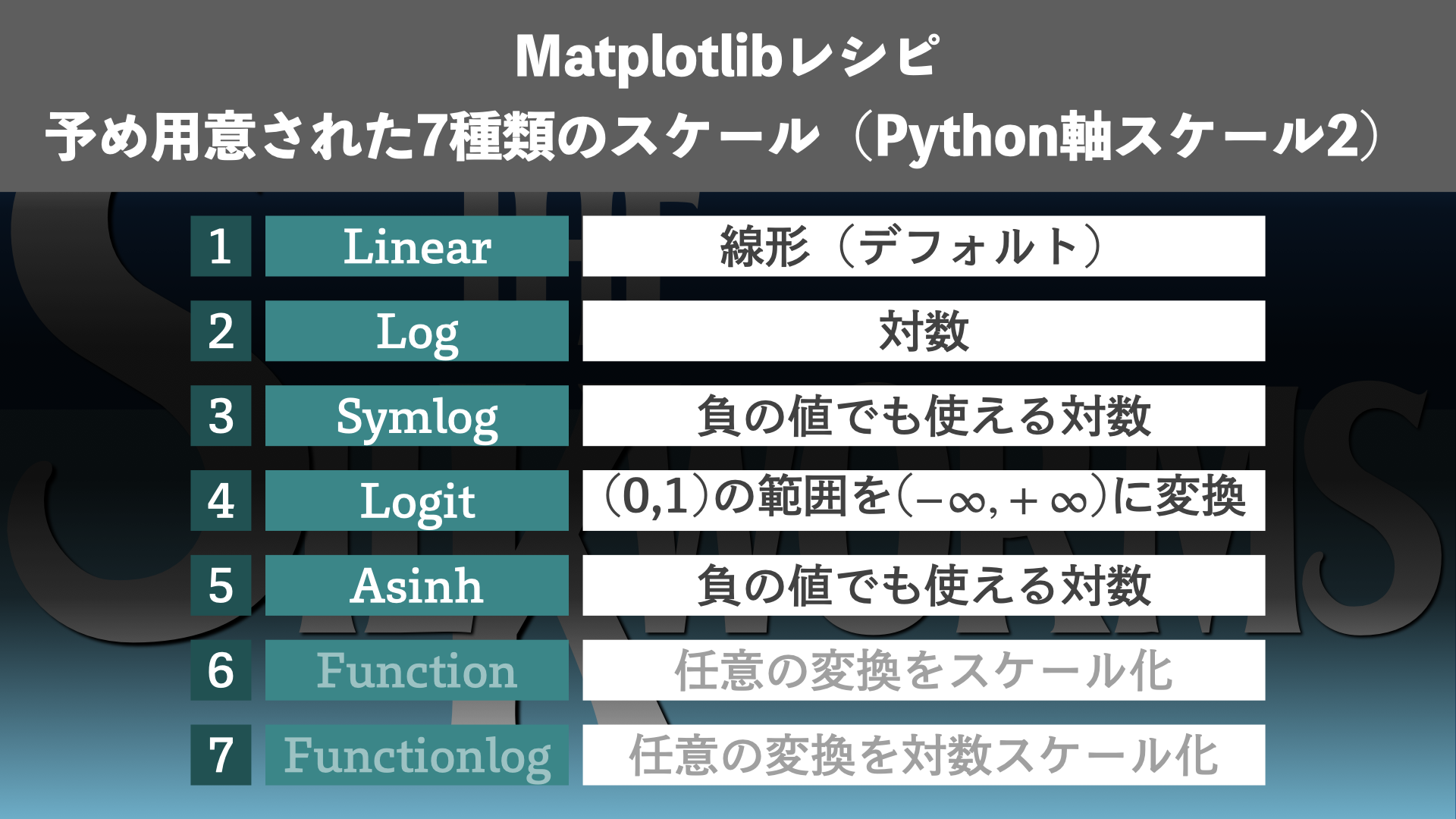
Matplotlibでは、予め7種類のスケール
- Linear: 線形(デフォルト)
- Log: 対数
- Logit: 0から1の範囲を\(-\infty\)から\(+\infty\)に変換
- Symlog: 負の値でも使えるlog変換
- Asinh: 負の値でも使えるlog変換
- Function: 任意の関数で変換
- Functionlog: 任意の関数で変換+log
が用意されています。これらのスケールであれば、軸のスケールを設定する際に
ax.set_yscale("log")などとすることで、簡単に設定することができます。
以下では上記のうち特に実用的なLog, Logit, Symlog, Asinhの4つについて、定義、挙動、使い方などの詳細を解説します!末尾にはPythonコードのサンプルも付けるのでご覧ください!
Background | 見やすい図を描くには適切な軸のスケール設定が必要
散布図やヒストグラム、その他さまざまな図を作る際、軸のスケールを適切に設定する必要があります。Pythonの作図ライブラリMatplotlibでは、デフォルトの線形スケール以外に様々スケールでプロットすることができます。プロットしたいデータの分布に合わせて適切なスケールを選ぶことが必要です。
前回記事「Matplotlib | Python作図での軸のスケール設定の必要性(Python軸スケール 1. 知識編)」では、具体例を交えて、
- 線形スケールで済む場面
- 対数(Log)スケールが必要な場面
- 対称対数(Symmetrical-log; symlog)スケールが必要な場面
をご紹介しました。どのような場合に線形スケールのままでよく、どのような場合にLogやSymlogを使う必要があるのかを知りたい方は前回記事をご覧ください!
今回の記事では、軸のスケール設定の必要性を理解したうえで、Matplotlibで予め用意されたスケールを実際に使う方法をコードのサンプル付きでご紹介します!
Method | 予め用意されたスケールの設定方法
Matplotlibで予め用意された7つのスケールのうち、実用的な4つ
- Log: 対数
- Logit: 0から1の範囲を\(-\infty\)から\(+\infty\)に変換
- Symlog: 負の値でも使えるlog変換
- Asinh: 負の値でも使えるlog変換
の定義と特徴を確認しつつ、実際のコードの書き方も紹介していきます。Jupyter Notebookを準備して一緒に進めていきましょう!参考までにJupyter Notebookの基本的な使い方は過去記事「python入門講座|pythonを使ってみよう2(Jupyter Notebookを使う方法)[第5回]」をどうぞ!
各種事前準備と確認
それぞれのスケールの紹介に入る前に、まずは準備や確認をしておきます。
ライブラリの準備
今回のコードで使うライブラリをインポートしておきます。以下をJupyter Notebookのコードセルで実行しておきます。
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspecなお、ライブラリは予めインストールしておく必要があります。ライブラリをインストールする方法については、過去記事「python入門講座 | Anacondaでpython3をMチップMacにインストールする方法[番外編]」と記事内のリンクをご参照ください。
Matplotlibのバージョン確認
ライブラリをインポートしたところでMatplotlibのバージョンを確認しておきます。以下を実行してみてください。
mpl._version.version以下のように出力されるはずです。
'3.8.0'
バージョン3.8以降では、今回紹介するスケールが全て用意されています。3.8未満では用意されているスケールの数が少ないのでご注意ください。バージョンが3.8未満になっている場合はアップデートをおすすめします。
予め用意されたスケールを確認する
Matplotlibで予め用意されたスケールは
mpl.scale.get_scale_names()で確認することができます。以下のように出力されるはずです。
['asinh', 'function', 'functionlog', 'linear', 'log', 'logit', 'symlog']
出力されるスケールの種類がこれよりも少ない場合にはMatplotlibのバージョンが3.8より古い可能性があるので確認してください。
さて、ここから各種スケールの定義と挙動を紹介していきます!
Linearスケール(線形)→省略
Linear(=線形)スケールはスケール変換を行わないことなので解説を省略します。MatplotlibのデフォルトのスケールはLinearスケールなので、何もしなければLinearスケールでプロットできます。
Logスケール(対数)
Logすなわち対数スケールを解説します。Logスケールは、プロットしたいデータの値の範囲が広い場合、すなわち値が10倍、100倍などと桁で異なる場合に適用すると綺麗に描画することができます。過去記事「Matplotlib | Python作図での軸のスケール設定の必要性(Python軸スケール 1. 知識編)」で例に上げた、
- 恒星の密度
- 鉱物の塊粒の寸法・重量
- 音の強さ
- 材料の寿命
- 生物群の個体数
- 生物個体の寸法・重量
- 市町村の人口
- 個人所得額
など、Logスケールは天文、地質、物理、生物、社会分野の様々なデータをプロットするのに適しています。以下で定義や関数型、プロット例を紹介します。
Log変換の定義の確認
Logスケールでは
$$
f(x) = \log_{a}(x) \tag{1}
$$
という変換が行われます。Matplotlibのデフォルトの底は\(a=10\)、すなわち常用対数スケールです。ここで、もとのデータ\(x\)の値は正つまり\(x>0\)である必要があります。
Log変換の関数型の確認
関数の様子をプロットして確認しておきましょう。以下を実行してください。
ax = plt.subplot(111)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title(r'$f(x) = \log_{10}(x)$')
x = np.logspace(-3,3,1000)
y = np.log10(x)
ax.plot(x, y)実行すると図1のような図が表示されます。Log変換では、10倍、100倍といった倍々の変化が+1、+2といった線形な変化に変わります。したがって、10倍、100倍と変化するものを比較するときにはLogスケールが便利です。過去記事「Matplotlib | Python作図での軸のスケール設定の必要性(Python軸スケール 1. 知識編)」も参考にご覧ください。
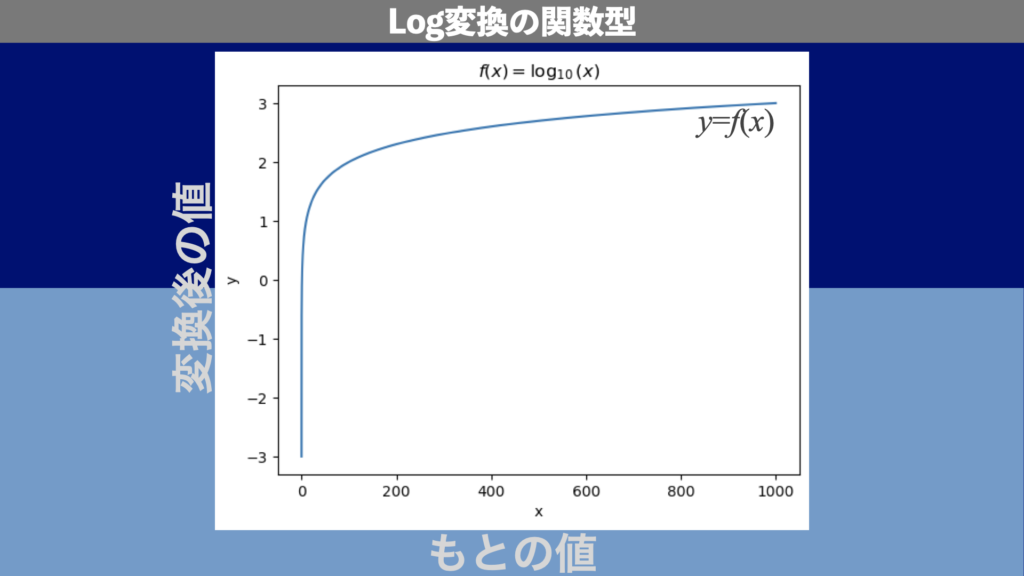
スケール設定の例をプロットする関数の用意
Logスケールの一例をプロットしてみましょう。プロットに際して、このあとLog以外にLogit, Simlog, Asinhでも同様にプロットするので関数を用意しておきます。線形スケールと所望のスケールで散布図を表示して比較する関数を作ります。あとでLogit, Simlog, Asinhの一例をプロットするときも同じ関数を呼び出します。
スケール設定の例をプロットする関数
以下を実行して関数`plot_example_scale`を定義しておいてください。スケール変換された状態で綺麗にプロットできる分布となっているデータを作成し、線形スケールと変換後のスケールそれぞれの散布図をプロットして比較します。引数に所望のスケール名称の文字列を取ります。
# plot example
def plot_example_scale(scale_trg:str):
# get x
x = np.random.normal(size=1000)
# get scale object
ax = plt.subplot(111)
mpl_scl = mpl.scale.scale_factory(scale_trg, ax)
plt.close('all')
# inverted transformer
mpl_invtrn = mpl_scl.get_transform().inverted()
y = mpl_invtrn.transform(x+np.random.normal(size=np.shape(x)))
# get figure
# plot with target-scale y
fig = plt.figure(figsize=[12,5])
gs = gridspec.GridSpec(1, 2, wspace=0.3)
axs = {}
# linear scale
i = 0
axs[i] = plt.subplot(gs[i])
axs[i].set_title('Example in linear scale')
axs[i].set_xlabel('x')
axs[i].set_ylabel('y')
axs[i].scatter(x, y)
# target scale
i = 1
axs[i] = plt.subplot(gs[i])
axs[i].set_title('Example in %s scale' % (mpl_scl.name))
axs[i].set_xlabel('x')
axs[i].set_ylabel('y')
axs[i].set_yscale(scale_trg)
axs[i].scatter(x, y)この関数plot_example_scaleでは、ランダムな1000個のデータ点の散布図を描画します。1000個のデータ点の\(x\)の値は正規分布に従い、\(y\)の値はスケール変換された状態で\(x\)と相関するようにします。1枚目のパネル(axs[0])では\(y\)軸はLinear(線形)スケール、2枚目のパネル(axs[1])では所望のスケールとなります。
x軸やy軸を所望のスケールに変更する方法
関数plot_example_scaleでは、y軸のスケールを
axs[i].set_yscale(scale_trg)の部分で設定しています。axs[i]はplt.subplotで生成されたMatplotlibのaxisオブジェクト、scale_trgは文字列”log”です。iは1です。つまり、
axs[1].set_yscale("log")と同じです。x軸をLogスケールにしたい場合には
axs[1].set_xscale("log")などとすればOKです。
Logスケールのプロット例
さきほど作成した関数`plot_example_scale`を実行して、Logスケールの場合のプロットを作ってみましょう。以下を実行します。
# plot
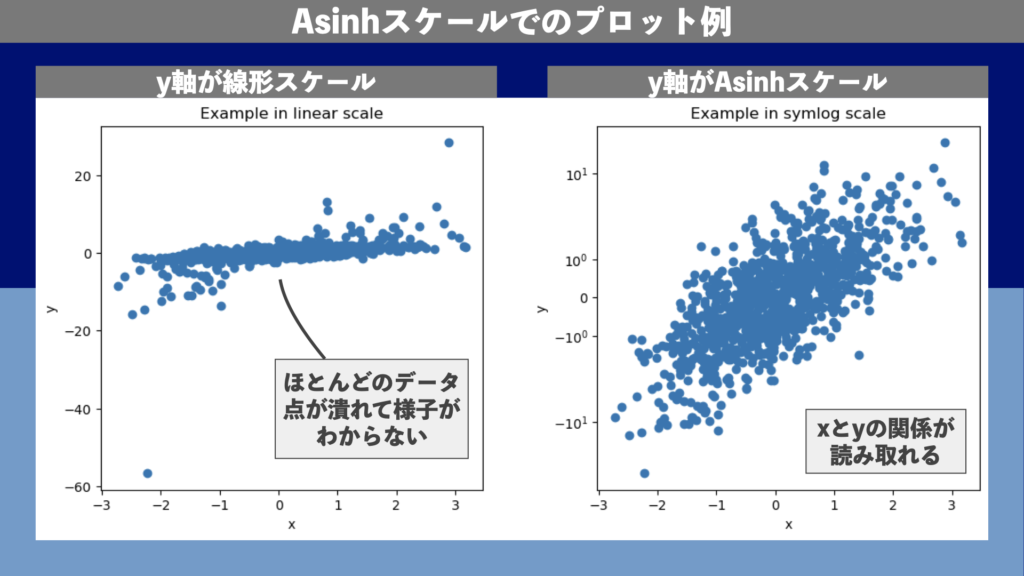
plot_example_scale('log')実行すると、図2のような図が生成されます。1枚目のパネルでは\(y\)軸が線形となっているため、ほとんどのデータ点が潰れてしまって、分布の様子がわかりません。ところが2枚目のパネルでは\(x\)と\(y\)の関係を読み取ることができます。
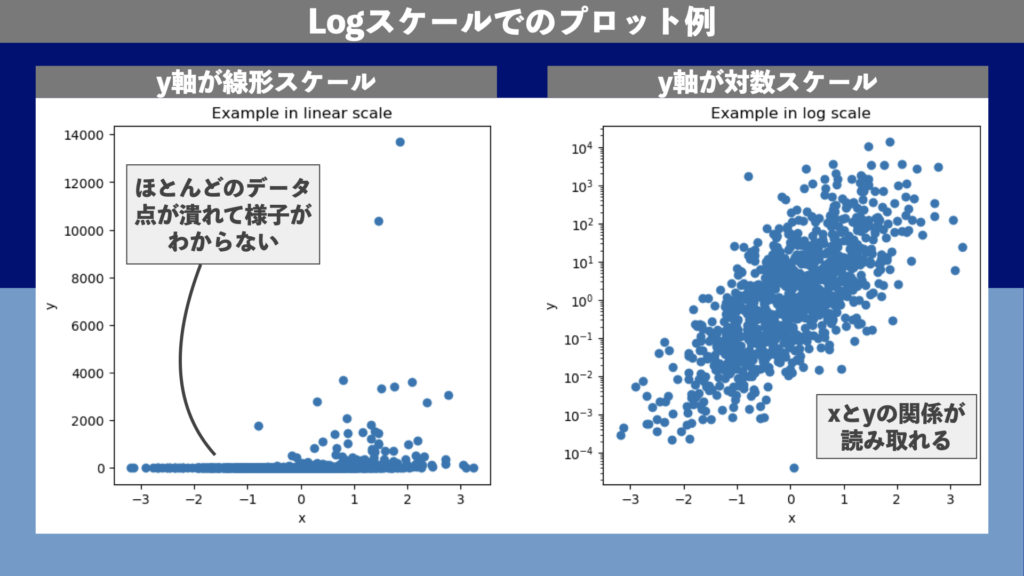
Logitスケール
Logitスケールを解説します。Logitスケールは(0,1)の範囲を(\(-infth, +infty\))に変換する関数です。データの値が(0,1)の範囲に収まる場合に適したスケールです。例えば、確率が当てはまります。以下で、定義と関数型、プロット例を紹介します。
Logit変換の定義の確認
Logitスケールでは
$$
f(x) = \log \left( \frac{x}{1-x} \right) \tag{2}
$$
という変換が行われます。対数の底は10すなわち常用対数です。Logit変換では、変換前の値が0.5付近では線形に近く、0と1付近ではLogスケールに近くなるように変換されます。変換の結果\((0,1)\)の範囲が\(-infty, +infty\)に変換されます。
Logit変換の関数型の確認
関数の様子をプロットして確認しておきましょう。以下を実行してください。
ax = plt.subplot(111)
ax.set_xlabel('x')
ax.set_ylabel('y')
x = np.r_[
np.logspace(-3,np.log10(0.5),1000),
np.logspace(np.log10(0.5),1-10**(-3),1000),
]
y = np.log10(x/(1-x))
ax.plot(x, y)実行すると図3のような図が表示されます。Logit変換では、0から1の範囲が\(-infty, +infty\)の範囲に変わります。例えば、0から1の範囲の値をとる確率と別の変数との相関を取りたい場合、確率の値をLogit変換しておくと良い場合があります。
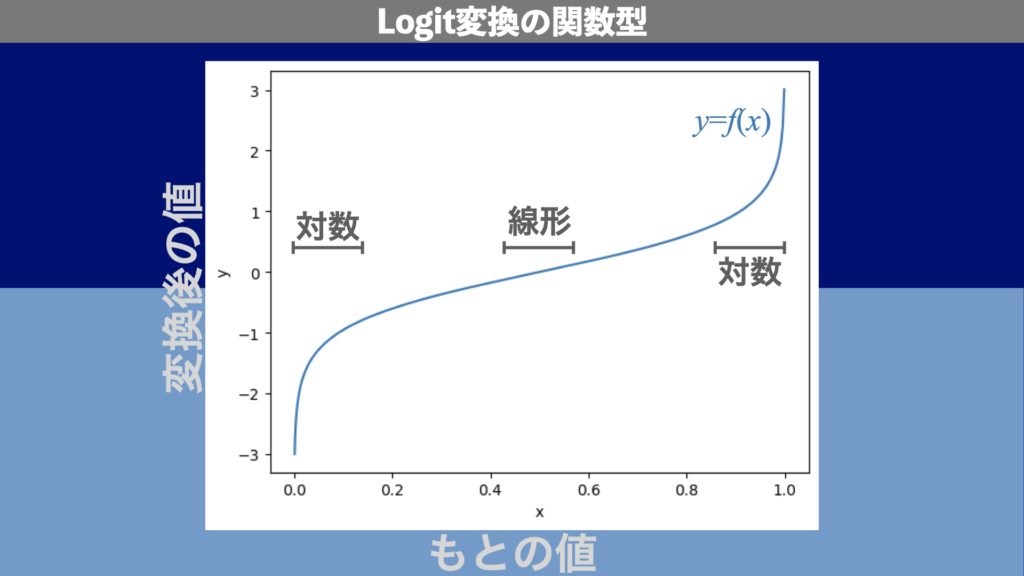
Logitスケールのプロット例
関数`plot_example_scale`を実行して、Logitスケールの場合のプロットを作ってみましょう。以下を実行します。
# plot
plot_example_scale('logit')引数に”logit”を取っているので、関数`plot_example_scale`の中では、
axs[1].set_yscale("logit")という操作が行われてy軸がLogitスケールに設定されます。
実行結果は図4のようになります。図2と比べると、左側のy軸が線形のパネルでも\(x\)と\(y\)に相関関係があることは読み取りやすいですが、Logitスケールの右側のパネルのほうが、\(x\)と\(y\)の関係を明確に読み取ることができます。
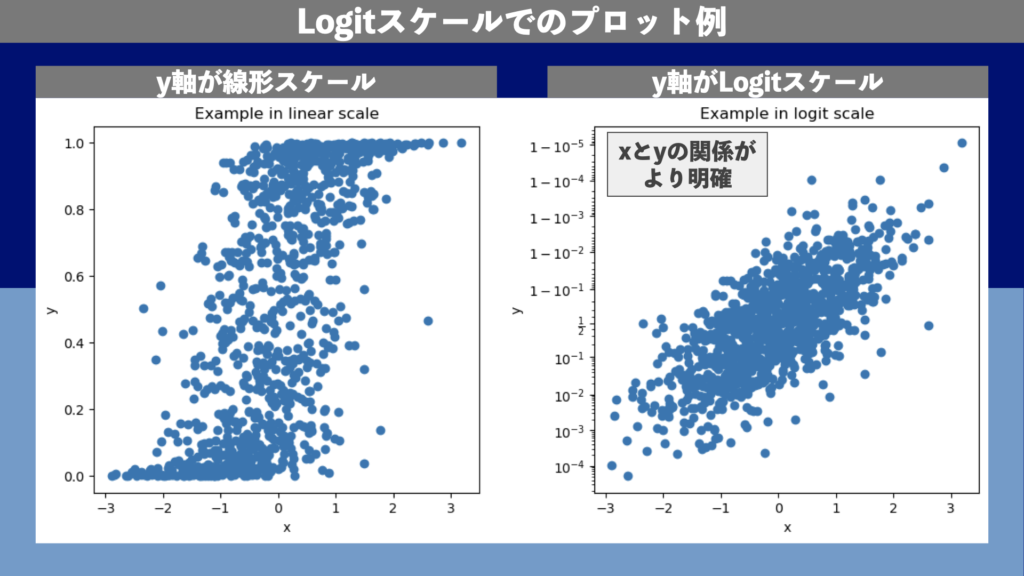
Symlogスケール(対称対数)
対象対数(Symmetrical-log; Symlog)スケールを解説します。Symlogスケールを使うと、負の値でもLogスケールでプロットすることができます。過去記事「Matplotlib | Python作図での軸のスケール設定の必要性(Python軸スケール 1. 知識編)」で例に上げた、市区町村の人口増減数はSymlogスケールでのプロットが適しています。Symlogスケールは
- データの値が10倍、100倍と桁で変わり、
- プラスの値もマイナスの値も取る
ような場合に適しています。もともと値の範囲が大きいものの変化率(速度や加速度)をプロットするのに適しています。以下では定義、関数型、プロット例を見ていきます。
Symlog変換の定義の確認
Symlogスケールでは
$$
\begin{align}
f(x) &=
\begin{cases}
\alpha x & (|x| < c)\\
\mathrm{sign}(x) c \left(
\alpha + \log_{a}(\frac{|x|}{c})
\right) & (|x| \geq c) \tag{3}
\end{cases} \\
\alpha &=
\frac{c}{1 – \frac{1}{a}} \tag{4}
\end{align}
$$
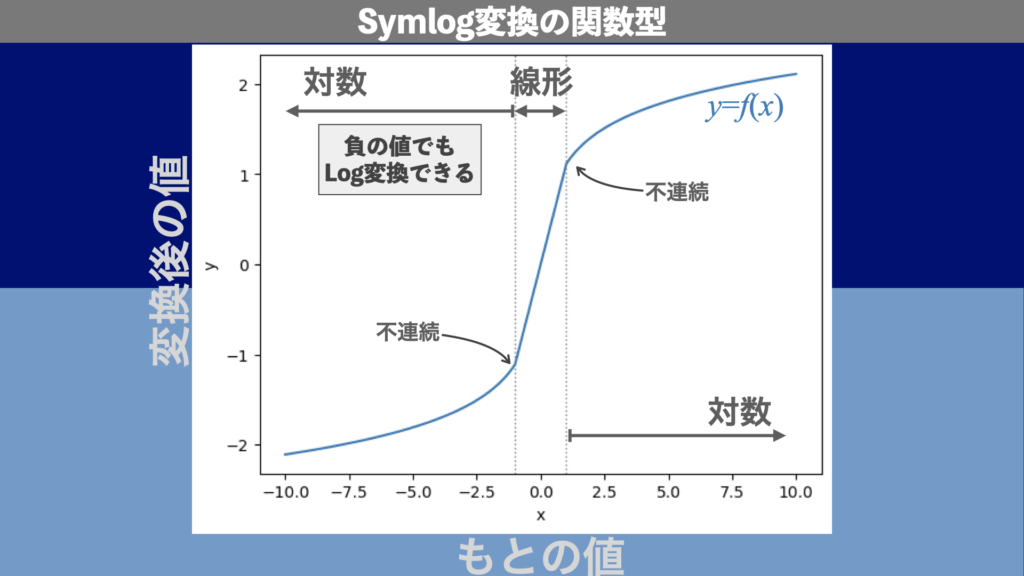
という変換が行われます。\(x\)が\(-c < x < c\)の範囲においては線形(\(f(x)=\alpha x\))に保たれ、\(x < -c\)や\(c < x\)の範囲においてはlogスケールに変換されます。
注意点としては\(x=c\)において、関数が連続でなくなります。簡単に言えば関数の形がカクッとなります。以下で関数型を確認して、この様子を確認してみましょう。
Symlog変換の関数型の確認
関数の様子をプロットして確認しておきましょう。以下を実行してください。
# set parameters
base = 10
linthresh = 1
linscale = 1
_linscale_ajd = (linscale / (1.0 - base**(-1)))
_log_base = np.log(base)
# set x
x = np.r_[
-np.logspace(1,np.log10(linthresh),1000),
np.linspace(-linthresh,linthresh,1000),
np.logspace(np.log(linthresh)/_log_base,1,1000)
]
# get y
y = _linscale_ajd * x
idx_log = np.where((x < -linthresh) | (x > +linthresh))
y[idx_log] = np.sign(x[idx_log]) * linthresh * (
_linscale_ajd +
np.log(np.fabs(x[idx_log])/linthresh) /
_log_base
)
# plot
ax = plt.subplot(111)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.plot(x, y)
# show threshold
ax.axvline(-linthresh, ls='dotted', lw=1.0, c='grey')
ax.axvline(+linthresh, ls='dotted', lw=1.0, c='grey')実行すると図5のような図が表示されます。Symlog変換では、負の値でもLog変換をすることができます。-cからcの範囲(図5ではc=1)で線形、その外側で対数という理解しやすい変換です。難点を挙げるとすれば、\(c\)を外から与える必要があるということと\(x=\pm c\)で不連続になることでしょう。これらが気になる場合には次に出てくるAsinhスケールを使いましょう。
Symlogスケールのプロット例
関数`plot_example_scale`を実行して、Symlogスケールの場合のプロットを作ってみましょう。以下を実行します。
# plot
plot_example_scale('symlog')引数に”symlog”を取っているので、関数`plot_example_scale`の中では、
axs[1].set_yscale("symlog")という操作が行われてy軸がSymlogスケールに設定されます。
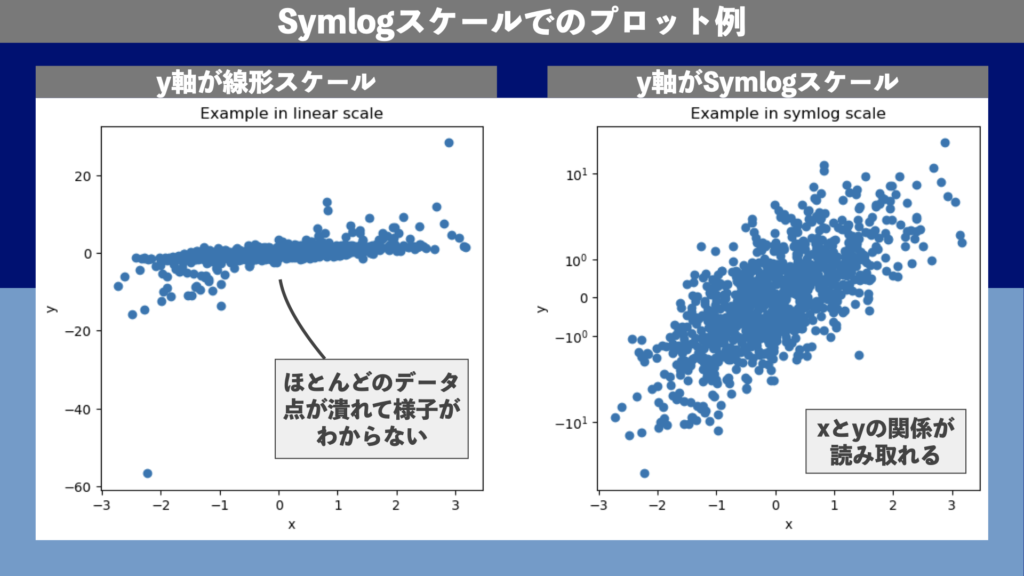
実行結果は図6のようになります。図6のデータには、\(y\)の値がプラスにもマイナスにも大きいものが少数存在します。そのため、左側の線形スケールのパネルでは、\(y\)の値が小さい大多数のデータが潰れてしまい、分布の様子がほとんどわかりません。一方、右側のSymlogスケールのパネルでは、分布の様子をはっきりと読み取ることができ、\(x\)と\(y\)の相関関係もよくわかります。
Asinhスケール
Asinhスケールは、Symlogと同様に、データの値がプラスにもマイナスにもなり、かつ10倍、100倍と桁で変化するような場合のプロットに適したスケールです。Symlogと同じように、もともと値の範囲が大きいものの変化率(速度や加速度)をプロットするのに適しています。Symlogとの違いは、変換関数が不連続になることがないことです。以下では、定義、関数型、プロット例を見ていきます。
Asinh変換の定義
Asinhスケールでは
$$
f(x) = x_0 \mathrm{arcsinh} \left(\frac{x}{x_0}\right) \tag{5}
$$
という変換が行われます。Symlogに比べるとシンプルです。後ほど詳しく述べますが、\(x \ll x_{0}\)の領域では線形に近づき、\(x \gg x_{0}\)では対数に近づきます。
ちなみに、Asinhは双曲線関数\(\sinh\)(ハイパボリックサイン)の逆関数(逆双曲線関数)のことです。双曲線関数\(\sinh\)は
$$
\sinh(x) = \frac{e^{x} – e^{-x}}{2} \tag{6}
$$
で、逆双曲線関数arcsinhは
$$
\mathrm{arcsinh}(x) = \ln \left( x + \sqrt{x^{2} + 1} \right) \tag{7}
$$
と表されます(\(\ln\)は底が\(e\)の自然対数)。
Asinh変換の関数型の確認
関数の様子をプロットして確認しておきましょう。以下を実行してください。
# set parameter
c = 1
# set x, y
x = np.r_[
-np.logspace(1,np.log10(c),1000),
np.linspace(-c,c,1000),
np.logspace(np.log10(c),1,1000)
]
y = c * np.arcsinh(x/c)
# plot
ax = plt.subplot(111)
ax.set_xlabel('x')
ax.set_ylabel('y')
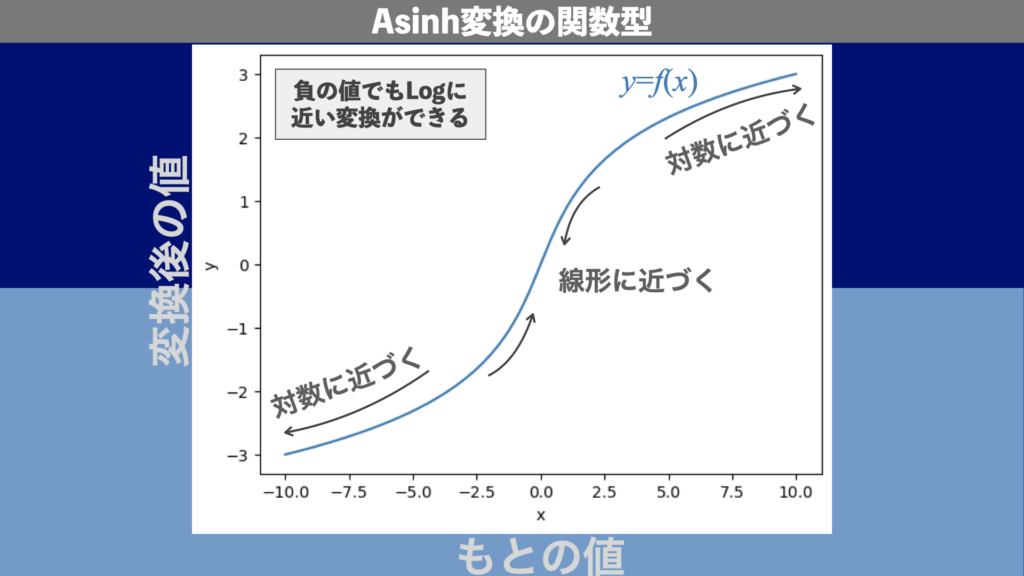
ax.plot(x, y)実行すると図7のような図が表示されます。図7を図5と比較すると、Asinh変換はSymlog変換を滑らかにしたような形になっていることがわかります。Asinh変換は負の値でも滑らかにLogに近い変換をすることができます。
Asinhスケールの特徴
AsinhスケールはSimlogと同様に、変数が正負どちらであっても用いることができ、絶対値が小さな値は線形が保たれ、大きな値はLogスケールに近い形に変換されます。数式で表すと
$$
f(x) \rightarrow
\begin{cases}
x & (|x| \ll x_{0})\\
x_{0} \mathrm{sign}(x) \ln|2 x| & (|x| \gg x_{0}) \tag{8}
\end{cases}
$$
となります。\(\ln\)は自然対数(対数の底は\(e\))です。
Asinhスケールの近似の確認
Asinhの近似式(8)が正しいことをプロットして確認しておきます。以下を実行してみてください。
# set parameter
c = 1
# set x, y
x = np.r_[
-np.logspace(1,np.log10(c),1000),
np.linspace(-c,c,1000),
np.logspace(np.log10(c),1,1000)
]
y = c * np.arcsinh(x/c)
# plot original asinh
ax = plt.subplot(111)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.plot(x, y, lw=6, c='silver', label='asinh')
# plot linear regime
c_lim = 0.5 * c
x1 = x[np.fabs(x) < c_lim]
y1 = x1
ax.plot(x1, y1, lw=4, label='linear')
# plot log regime
c_lim = 2 * c
x2 = np.array([x[x < -c_lim], x[x > c_lim]]).T
y2 = np.sign(x2) * c * np.log(2 * np.fabs(x2)) / c
ax.plot(x2, y2, lw=4, c=plt.rcParams['axes.prop_cycle'].by_key()['color'][2], label=['log', None])
# legend
ax.legend()変数cが式(8)の\(x_{0}\)なので、Asinhの関数型を\(- \frac{1}{2} x_{0} < x < \frac{1}{2} x_{0}\)の範囲では線形と、\(x < – 2 x_{0}, 2 x_{0} < x\)の範囲では対数と比較するプロットを作成しています。上記を実行すると図8が得られます。図8では、Asinhを灰色、線形(\(y=x\))を
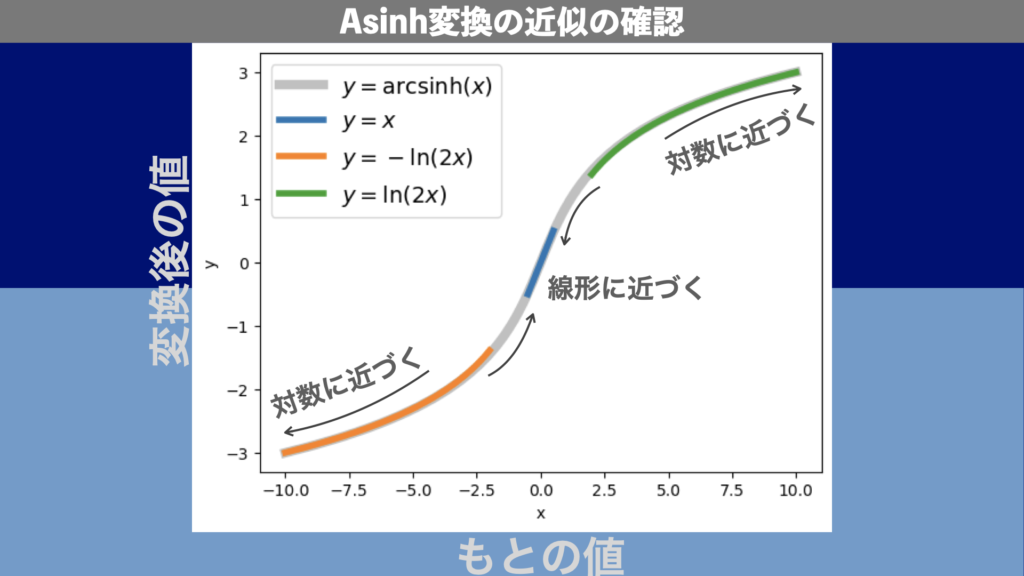
Asinhのメリット・デメリット(Symlogとの比較)
Asinh変換は、値の正負にかかわらずlogに近い変換を行うことができる点において、Symlog変換とよく似ています。AsinhはSymlogと比較して、
- \(x = c\)で連続になる
というメリットがある一方で、
- \(|x| \gg x_{0}\)で近似される対数領域において、任意の底(特に常用対数)を取ることができない
というデメリットもあります。変換関数の連続性を保ちたい場合にはAsinhを使い、常用対数を採用したい場合にはSymlogを使うなどと、状況に応じてAsinhとSymlogを使い分けるのが良いでしょう。
Asinhスケールのプロット例
関数`plot_example_scale`を実行して、Asinhスケールの場合のプロットを作ってみましょう。以下を実行します。
# plot
plot_example_scale('asinh')引数に”symlog”を取っているので、関数`plot_example_scale`の中では、
axs[1].set_yscale("asinh")という操作が行われてy軸がAsinhスケールに設定されます。
実行結果は図9のようになります。Simlogのプロット例の図6とほぼ同じプロットとなっていることがわかるはずです。Asinhスケールでは、Symlogスケールのときと同様、プロットしたいデータがプラスとマイナス両方の値を取り、かつ10倍、20倍と倍々で増加・減少するようなダイナミックレンジの広い場合でもわかりやすくプロットすることができます。
FunctionスケールとFunctionlogスケール
Matplotで予め用意されているスケールは、これまでに紹介してきた5つに加えて
- Functionスケール
- Functionlogスケール
の2つを加えた7つです(matplotlib version 3.8)。Functionスケールでは、任意の関数とその逆関数を与えることで、任意の変換のスケールを使うことができます。またFunctionlogスケールでは、任意の関数で変換したものをさらにLog変換するというスケールを使うことができます。
FunctionスケールとFunctionlogスケールは使い勝手が良くない
ただし、FunctionスケールとFunctionlogスケールは使い勝手が悪く、私自身は実用性を感じたことがないので、ここでは詳細を解説しません。具体的には
- 複数の任意のスケールを登録できない
- 文字列でスケールを呼び出すことができない
- 軸の目盛りを適切に調整することができない
といったデメリットがあり、あえてFunctionスケールやFunctionlogスケールを使おうとは思いませんでした。
任意の変換をスケールとして使うならCustom Scaleを作成したほうが良い
もし任意の変換をスケールとして使うならCustomスケールの機能を使って、独自の名前のスケールを作ったほうが使いやすいです。Customスケールについては次回以降で解説するので、どうぞお楽しみに!
Result | Pythonのサンプルコード
今回のPythonコードの実装例を掲載します(Jupyter Notebook)。参考にどうぞ!
Conclusion | まとめ
最後までご覧頂きありがとうございます!
Pythonの作図ライブラリMatplotlibで予め用意されたスケールを紹介しました!
Matplotlibでは、予め7種類のスケールが用意されています。これらのスケールであれば、軸のスケールを設定する際に「ax.set_yscale("log")」などと記述することで、簡単に設定することができます。Logスケールだけでなく、負の値でもLogに近い表示ができるSymlogやAsinh、確率のプロットに適したLogitスケールなど、便利なものが用意されています。状況に応じて使い分け、説得力のある図を作りましょう!
以上「Matplotlib | 予め用意された7種類のスケール(Python軸スケール2)」でした!
またお会いしましょう!Ciao!

コメント