Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
今回はpythonで綺麗な散布図を描く方法の第2回です!2次元の散布図上の点の密度をカラーで表示する方法8つを、背景の考え方とともにまとめてご紹介します!密度カラー散布図の描き方は、密度計算の方法やスムージング、個々の点への密度の割当方法で8つに分類することができます。今回はこれらを網羅的にご紹介します。
この記事を読めば、pythonで綺麗な2次元散布図をプロットする方法を知ることができます!ぜひ最後までご覧ください。

この記事はこんな人におすすめ
- Pythonでデータ解析をしている
- 散布図を綺麗に描きたい
- Abstract | カラー密度散布図を描く8つの方法
- Method | 密度カラー散布図を描く方法のポイントと分類
- Result | 綺麗な散布図を描く方法8分類
- 8つの方法による密度カラー散布図の描画例
- 方法1 | 2次元ヒストグラム(密度計算: ヒストグラム、スムージング: なし、点への割振り: なし)
- 方法2 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: なし、点への割振り: 線形補間)
- 方法3 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: なし、点への割振り: Digitize)
- 方法4 | 2次元ヒストグラム(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: なし)
- 方法5 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: 線形補間)
- 方法6 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: Digitize)
- 方法7 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: KDE、点への割振り: N/A)
- 方法8 | 密度カラー散布図(密度計算: KDE、スムージング: N/A、点への割振り: N/A)
- 今回の図を作成したコードのサンプル
- 8つの方法による密度カラー散布図の描画例
- Conclusion | まとめ
- References | 参考文献と関連記事
Abstract | カラー密度散布図を描く8つの方法
データ点が多い場合に、2次元散布図を綺麗に表示するには点の密度をカラーで表示する「密度カラー散布図」が便利です。密度カラー散布図の描き方は
- 密度の計算方法
- スムージングの方法
- 個々の点への密度の割当方法
によって8つに分類することができます(図1)。
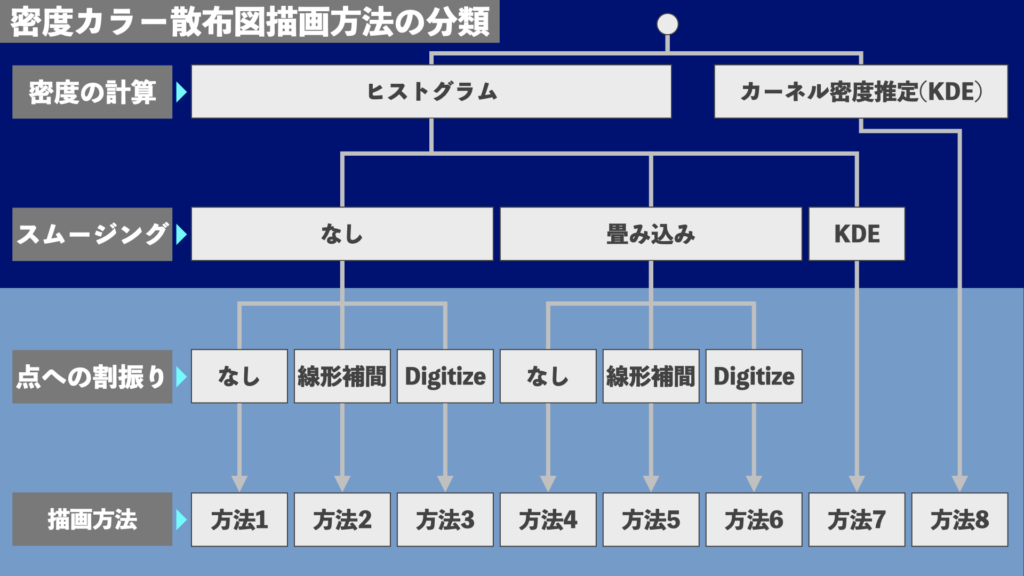
この記事では8つの方法の概要とそれぞれのメリット・デメリットをご紹介します。それぞれ、実装しやすさ、様々なデータへの対応のしやすさ、計算速度などに一長一短があります。私の見解としては、方法5
- ヒストグラムで密度を計算
- 畳み込みでスムージング
- Digitizeで点に割振り
が様々な場面で使えるのでおすすめです。ただし、実装する際のコードが長くなるデメリットもあります。今回、一通りの方法をご紹介するので、それぞれどのようなメリット・デメリットがあるかご理解いただければ幸いです。
なお、この記事は理論編として概要を説明します。実際のコードの書き方を知りたい方は本シリーズ次回以降の下記記事
をご覧ください!
Method | 密度カラー散布図を描く方法のポイントと分類
密度カラー散布図を描く上でポイントとなるのが、
- 密度の計算方法
- スムージングの方法
- 個々の点への密度の割当方法
の3点です。以下ではこの3点について詳しく見ていきます。
密度の計算方法 | ヒストグラム or カーネル密度推定(KDE)
密度カラー散布図を描く際には、\((x,y)\)のデータ点から、座標上の各点における密度を計算します。密度を計算するために
- 2次元ヒストグラムを使う
- カーネル密度推定(Kernel Density Estimation, KDE)を使う
という選択肢があります。
それぞれの密度計算方法のメリット・デメリット
ヒストグラムとKDEには、それぞれメリットとデメリットがあるので、状況に合わせて使い分ける必要があります。ヒストグラムとKDEの主なメリットとデメリットは表1のとおりです。特にKDEは計算速度が大きな弱点です。データ点の数が多い場合、KDEでは時間がかかりすぎるのでヒストグラムを使うことになります。
| メリット | デメリット | |
| ヒストグラム | 1. 計算が速い 2. 非線形なx, yスケール(logなど)にも対応可 | 1. 滑らかに描画するには後工程でスムージングが必要 2. 低密度の領域を描画するには後工程で点への割振りが必要 |
| KDE | 1. 後工程なしで滑らかに描画できる 2. 後工程なしで低密度の領域も描画できる | 1. 計算が遅い 2. 非線形なx, yスケールへの対応が複雑になる |
2次元ヒストグラムを使った密度計算の概要
2次元ヒストグラムを使って、座標上の各点における密度を計算する概要を示します。\(x, y\)座標上にメッシュ状のビンを設定して、ビンあたりのデータ点の数を計測することで密度を計算します(図2)。
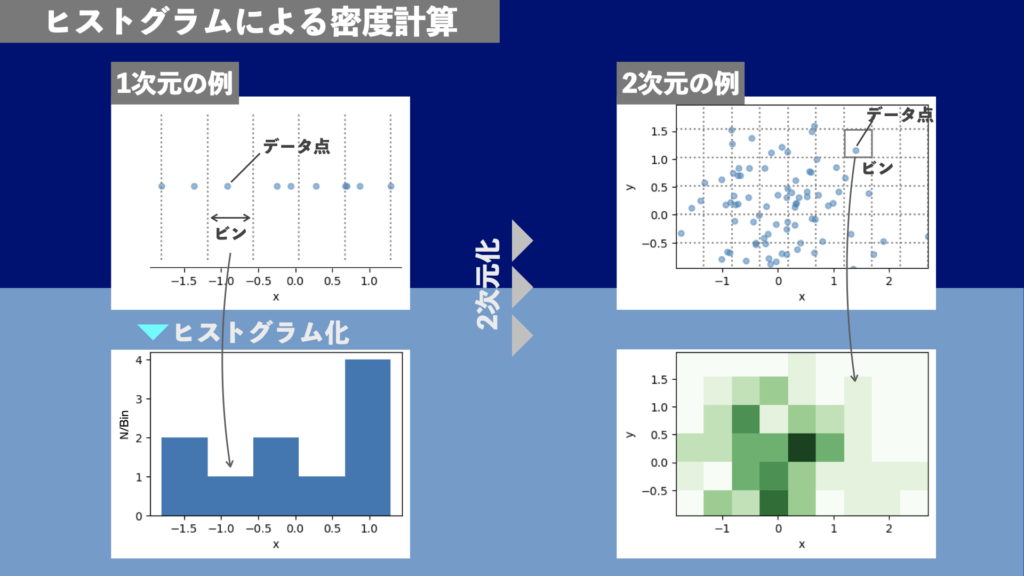
カーネル密度推定(KDE)による密度計算の概要(方法8)
座標上の密度を計算するもう一つの方法として、カーネル密度推定(Kernel Density Estimation, KDE)があります。密度の計算にKDEを使う場合、後段のスムージングや点への割当を考慮する必要はありません(図1)。KDEで密度分布を推定し、各点での密度を計算するだけで密度カラー散布図を描くことができます。これは図1の分類では方法8にあたります。
KDEによる密度の計算は、ヒストグラムを使う方法に比べて少し複雑なので詳しく説明していきます。
KDEでは、母集団の密度分布を推定する
KDEは、サンプルの母集団(データ点の集合が抽出されたもととなる集合)の密度分布を推定する方法、つまりデータ点の背景にある密度分布を推定する手法です(データ点そのものの分布を示すためのものではありません)。KDEはノンパラメトリックな母集団の密度分布の推定方法の代表的な方法です。ノンパラメトリックとは、母集団の密度分布の形を事前に仮定しない方法です。これとは逆のパラメトリックな手法としては、母集団の密度分布として正規分布、指数分布、ガンマ分布といった特定の分布関数を仮定するものが挙げられます。
KDEの定義
KDEでは、母集団の密度がそれぞれのデータ点が形成するカーネルの重ね合わせとして表現されます。データが1次元の場合、KDEによる密度推定では、密度関数\(\hat{p}(x)\)はカーネル関数\(K\)を用いて
$$
\hat{p}(x) = \frac{1}{n h}\sum_{i}^{n}K\left(\frac{x-X_{i}}{h}\right) \tag{1}
$$
と表されます。\(n\)はデータ点の数、\(h\)はバンド幅と呼ばれ、事前に適切に設定すべきパラメータ、つまりKDEにおけるハイパーパラメータです。この式から、\(p(x)\)はそれぞれのデータ点が張るカーネル\(K\left(\frac{x-X_{i}}{h}\right)\)の重ね合わせ(=足し算)となっていることがわかります。KDEの中でも、カーネル関数がGaussianであるものをGaussian KDEと呼びます。Pythonではscipy.stats.gaussia_kde()で実装されています。
KDEの概念図
KDEによる密度推定の様子を図にしたものが図3です。図3左側の1次元の例では、3つのデータ点それぞれが作るGaussianカーネルの重ね合わせとなっていることが良くわかります。これを2次元に拡張したものが図3右側です。こちらは10個のデータ点があり、それぞれが2次元のGaussianカーネルを形成し(図3右中段)ます。最終的な密度はこれらのカーネルの重ね合わせ(図3右下段)として表現されます。
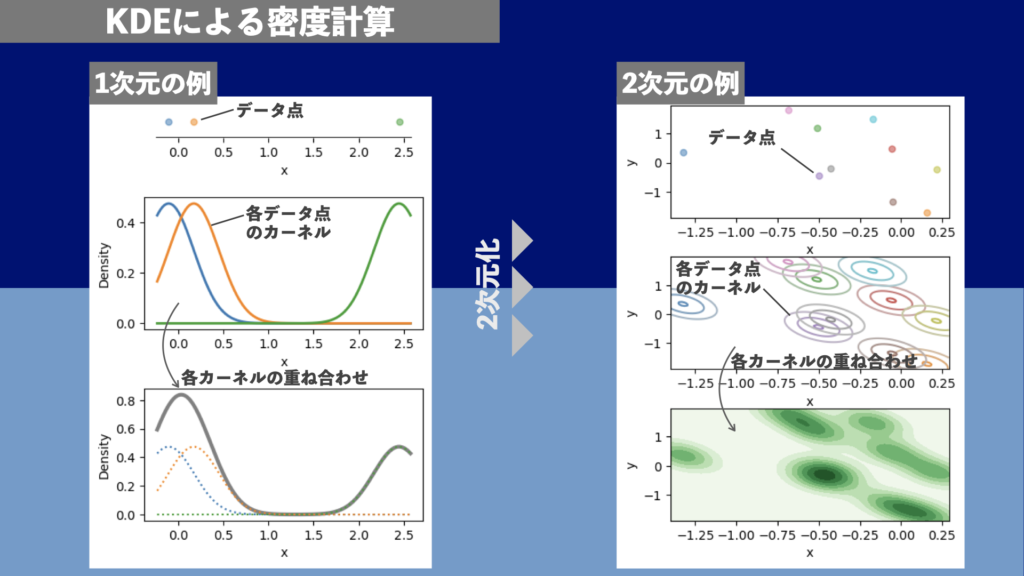
KDEについてもっと知りたい方は末尾の参考文献をご覧ください。東京大学の講義資料はわかりやすく、バンド幅の推定方法まで掲載されています。ご興味がある方は目を通していただくと良いでしょう。
スムージング方法 | なし or 畳み込み or KDE
ヒストグラムで密度の計算を行った場合、スムージングを行うことで滑らかに描画することができます。スムージングの方法として、
- スムージングなし
- 畳み込み(convolution)
- カーネル密度推定(KDE)
があります。
それぞれのスムージング方法のメリット・デメリット
スムージングを行うか行わないか、スムージングを行う場合に畳み込みを使うかKDEを使うかには一長一短があります。主なメリット・デメリットは表2の通りです。
| メリット | デメリット | |
| スムージングなし | 1. 実装が単純 2. 追加の計算がないため最も高速 | 1. 滑らかな密度分布とならない |
| 畳み込み | 1. 滑らかな密度分布が得られる 2. KDEよりも計算が高速 3. 非線形なx, yスケールへの対応が容易 | 1. 実装の手間がかかる 2. スムージングの計算時間がかかる |
| KDE | 1. 滑らかな密度分布が得られる 2. カラーに密度以外を割り当てる際に有効(応用編) | 1. 実装の手間がかかる 2. 畳み込みよりも計算が遅い 3. 非線形なx, yスケールへの対応が複雑になる |
密度カラー散布図を描く場合、ここでKDEを使うメリットはあまりなく、畳み込みで事足ります。ただし、カラーに密度以外の量を割り当てる場合はKDEが有効なことがあります。これは密度カラー散布図の応用で、(\(x, y, z\))というデータが存在するとき、各(\(x, y\))での\(z\)の平均値を知りたい場合や\(z\)と(\(x, y\))との関係を調べる場合に有効です。ここでは詳しくは扱いませんが、このシリーズの最後に扱う予定です。
スムージングなしの場合
スムージングをしない場合、前段のヒストグラムを作成した際のビンの形が密度カラー散布図にそのまま現れることになります。後段の点への割当で線形補間を使うと滑らかに描画ができますが、そうでない場合はヒストグラムのビンの形がくっきりと描画されます。
畳み込みでスムージングする場合
ヒストグラムを2次元画像として、畳み込みを使ってスムージングをすることで、滑らかに描画することができます。ヒストグラムの畳み込みを理解するため式を書いてみます。まず1次元の畳み込みは、\(x_{i}\)でのヒストグラムの値を\(p(x_{i})\)、畳み込みのカーネル関数を\(K\)として、
$$
q(x_{i}) = \sum_{j} p(x_j) K\left(x_{i} – x_{j}\right) \tag{2}
$$
と表すことができます。式(2)は、位置\(x_{j}\)での値\(p(x_{j})\)が、畳み込み後の位置\(x_{i}\)での値\(q(x_{i})\)にどの程度寄与するかを表しています。寄与の割合がカーネル関数\(K\)で与えられます。すなわち\(K\)は\(p(x_j)\)の重みを与えます。\(K\)は重みの和が1になる条件すなわち\(\sum K\left(x_{i} – x_{j}\right) = 1\)を満たす必要があります。\(K\)としては例えばGaussianが想定されます。
式(2)を2次元に拡張すると、
$$
q(x_{i}, y_{j}) = \sum_{k,l} p(x_{k}, y_{l}) K(x_{i} – x_{k}, y_{j} – y_{l}) \tag{3}
$$
となります。この式は2次元の画像の畳み込みの式です。この式も、位置\((x_{k}, y_{l})\)での値\(p(x_{k}, y_{l})\)が、畳み込み後の位置\((x_{i}, y_{j})\)にどの程度寄与するかを表すしています。
ヒストグラム畳み込みの概念
1次元と2次元のヒストグラムを畳み込みでスムージングする概念図を図4に示します。
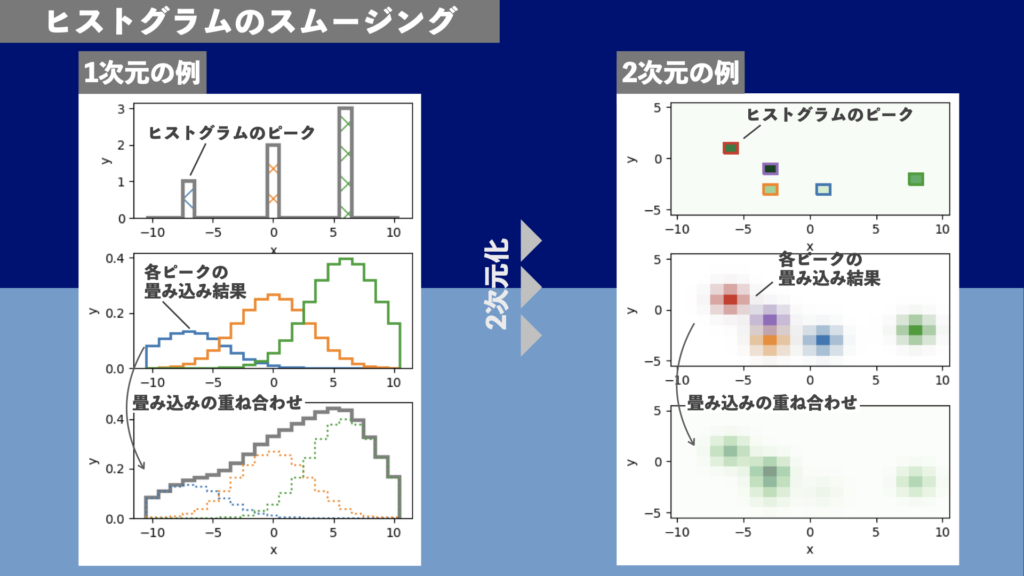
図4左側の1次元の例は3つのピークを持つヒストグラムです(図4左上)。このヒストグラムに畳み込みを掛けると、ヒストグラムの各点の畳み込み結果が得られます(図4左中)。この例では3つのピーク以外の値はゼロなので、3つのピークそれぞれをGaussianで畳み込んだ結果が得られます。オレンジの分布を見るとGaussianの形がよくわかります。ヒストグラム上のすべての点について畳み込みを行い、それを重ね合わせたものがスムージングされたヒストグラムとなります(図4左下)。この例ではつのピーク以外の値はゼロなので、3つのピークそれぞれを畳み込んだ結果を足し上げたものが得られます。
図4右側は2次元に拡張した例です。図4右上は2次元ヒストグラムで、緑色の濃いセルほど値が大きいことを表しています。色線で囲まれた5つのセル以外の値はすべて0です。この2次元ヒストグラムを畳み込みます。5つのピークそれぞれを畳み込んだ結果が図4右中です。2次元のGaussianで畳み込んでいるので、描くピークの周りにガウシアンの形が現れています。すべての点について畳み込んだ結果を重ね合わせたのが図 4右下です。この例では、5つのピーク以外はすべて0なので、5つのピークを畳み込んだ結果を足し合わせた結果となります。
ヒストグラムの畳み込み = データ点の圧縮 + KDE
ヒストグラムを畳み込むことは、データ点を圧縮してからKDEを行うことと同義です。式(2)をKDEの式(1)と比べてみてください。式(2)は式(1)と同じ形をしており、\(p(x_j)\)が追加されたにすぎません。KDEの式(1)も、各点が持つ重み\(w(X_{i})\)を含めて書くと
$$
\hat{p}(x) = \frac{1}{n h}\sum_{i}^{n} w(X_{i}) K\left(\frac{x-X_{i}}{h}\right) \tag{4}
$$
となります。これは式(2)と全く同じです。最初からKDEを使う方法8(図1の分類参照)と、ヒストグラム化してからスムージング(+点への割当)を行う方法5, 方法6, 方法8は本質的には同じことになります。ちなみに次に紹介するヒストグラムにKDEを適用する方法7も同じ式になります。
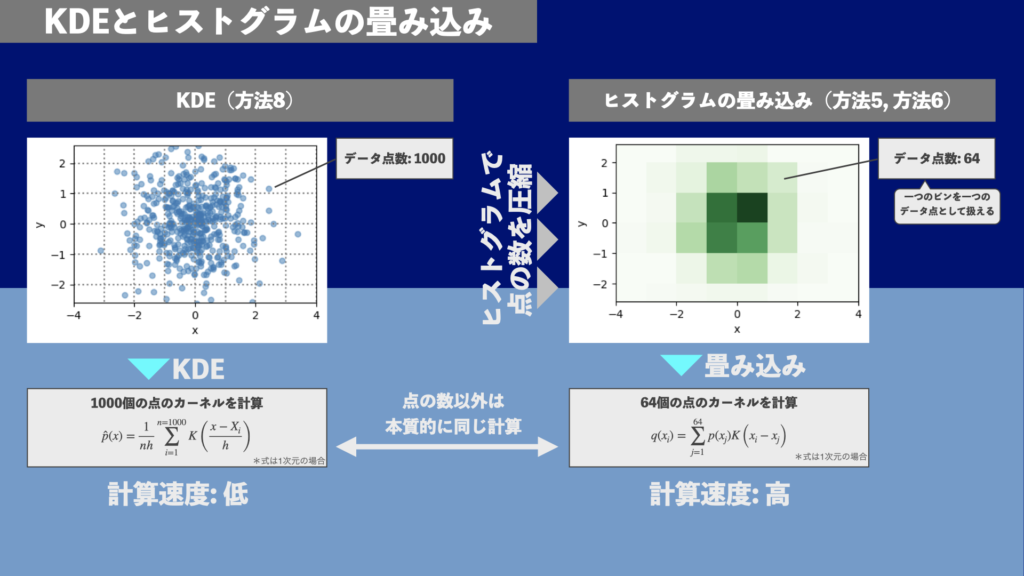
ヒストグラムのスムージングがKDEと同義なので、データ数が多くてKDEをしようとすると時間がかかりすぎる場合には、ヒストグラムのスムージングが有効な対策となります。ヒストグラムのスムージング(図1: 方法5, 方法6, 方法7)とKDE(図1: 方法8)は本質的には同じ計算をしていることになりますが、ヒストグラム化しておくことでデータ点の数をビンの数に圧縮することができます(図5)。2次元のデータ点を2次元ヒストグラムにしてデータ点を圧縮ことで、KDEの弱点である
- データ点が多いときに計算速度が遅くなる
ことを克服することができます。データ点の数が少なくためヒストグラムのスムージングのほうが計算速度が圧倒的に早くなります。
KDEでスムージングする場合
ヒストグラムを2次元画像として畳み込む以外に、ヒストグラムの各点をデータ点として扱ってKDEを適用することもできます。ビンの中心座標をデータ点の座標\((x, y)\)、重み\(w(x,y)\)をヒストグラムの値としてKDEを適用します。概念図を図6に示します。図5とほとんど変わらないことがわかります。ヒストグラムのKDEも本質的にはヒストグラムの畳み込みと同様に、ヒストグラム化することによるデータ点の数の圧縮です。ヒストグラムの畳み込みと同様、KDEをそのまま使う方法8(図1の分類参照)と比べて計算の高速化の恩恵を受けることができます。
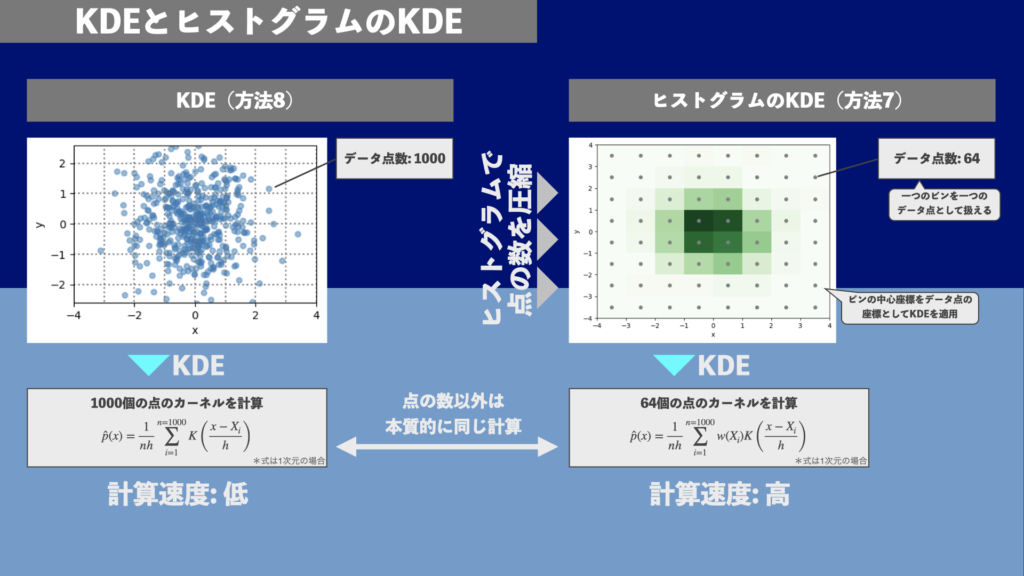
図6では、1000個のデータを8\(\times\)8のビンでヒストグラム化することで64個のデータに圧縮しています。簡単のためビンの中心をデータ点の座標としました。もとのデータにKDEを適用するのと、ヒストグラム化後にKDEを適用するのでは、もとのデータ点の座標とビンの中心座標のズレの分だけ結果が変わります。ただし、この例では見やすくするため粗いビンを切りましたが、ビンが十分に細ければ座標のズレは小さくなります。また、少し応用になりますが、ヒストグラム化後のデータの座標をビンの中心ではなく、ビンの中のデータ点の重心とすることでより厳密にもとのデータのKDEに近づけることも可能です。
点への割振り方法 | なし or 線形補間 or Digitize
ヒストグラムを使う場合、点への割振りを行うか否かで密度カラーヒストグラムの見え方が変わります。ここでの選択肢は
- 点への割振りを行わない
- 線形補間で割振り
- Digitizeで割振り
の3つです。
それぞれの点への割振り方法のメリット・デメリット
点への割振りを行うか否か、行う場合に線形補間かDigitizeかのメリット・デメリットをまとめます。
| メリット | デメリット | |
| 点への割振りなし | 1. 実装が単純 | 1. 密度が低い場所の様子がわからない |
| 線形補間 | 1. 密度の低い場所まで描画できる 2. ヒストグラムのビンの形が現れない | 1. 実装の手間がかかる 2. 座標軸のスケールが線形でないときの対応がDigitizeに比べて面倒 |
| Digitize | 1. 密度の低い場所まで描画できる 2. 座標軸のスケールが線形でなくても同じように実装できる | 1. 実装の手間がかかる 2. ヒストグラムのビンの形が現れる |
点への割振りを行わない場合、普通のヒストグラムのプロットになります。普通のヒストグラムは、実装は単純ですが、データ点の密度が低い領域の様子がわからなくなるデメリットがあります。線形補間やDigitizeを使って点への割振りを行うことで、密度の高いところから低いところまで高い視認性で描画することができるようになります。線形補間とDigitizeの違いは、ヒストグラムのビンの形が描画に現れるか否か、座標軸のスケールが非線形の場合に対応しやすいか否かといったところになります。
点への割振りなしの場合 | 方法1・方法4
点への割振りを行わない場合、普通にヒストグラムを描くのと同じことになります。点への割振りを行わないパターンは、図1の方法1と方法4に該当します。表4に方法1と方法4についての、密度の計算、スムージング、点への割振りのパターンをまとめました。
| 方法1 | 方法4 | |
| 密度の計算 | ヒストグラム | ヒストグラム |
| スムージング | なし | 畳み込み |
| 点への割振り | なし | なし |
点への割振りを行わないプロットの例(方法1・方法4)
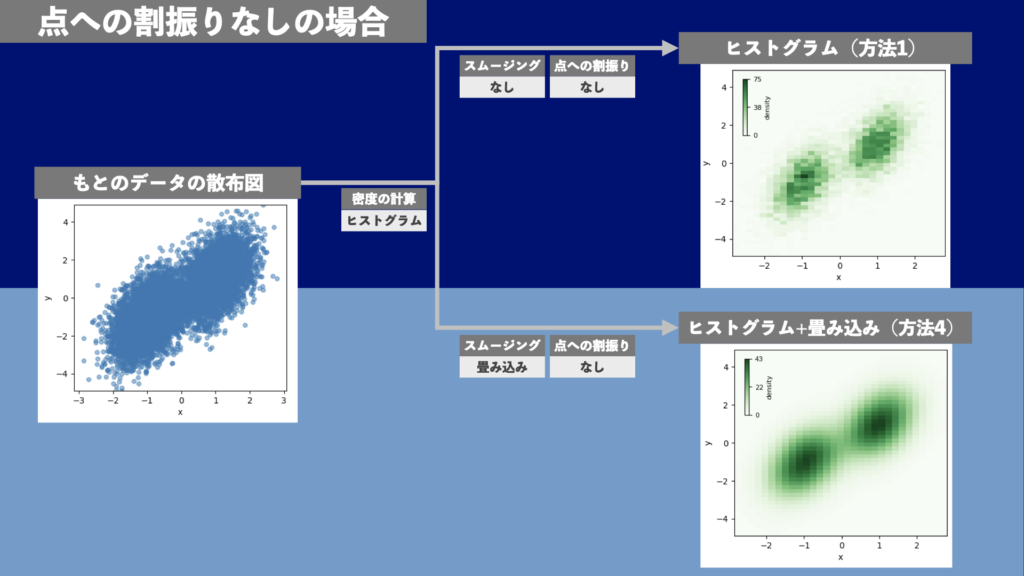
方法1と方法4で描画した例を図7に示します。データは前回記事「Matplotlib | 綺麗な2次元散布図の描き方1(概要編)」の「データ2: 普通の散布図では様子がわかりにくい双峰分布の例」です。ヒストグラムやヒストグラム+畳み込みで描画すれば、双峰分布であることがわかります。一方で、点への割振りを行わない場合、点が少ない場所の様子がわからなくなります。ヒストグラムをそのままプロットしたもの(図7右上)と畳み込んだもの(図7右下)を比べると、畳み込んだものは滑らかになっていることがわかります。このデータは正規分布2つを合わせた双峰分布なので、背景の分布は滑らかなものです。畳み込みを行うほうが、データ点の裏側にある本来の背景の分布に近いものを表示できていると言えます。
線形補間で点への割振りを行う場合 | 方法2・方法5
点への割振りを行うことで、密度カラー散布図を描くことができます。ヒストグラムで計算した密度をデータ点に割り振る際、線形補間を使うことができます。この方法では、ビンの中心座標における密度の値をそのビン内の密度とします。任意の点での密度の値は、周囲のビンの中心座標における密度から線形補間で求めます。1次元の場合を例にとって線形補間を式にすると、ビンの中心座標を\(X_{i}\)、そこでの密度を\(Y_{i}\)とすると、任意の点\(x\)(\(X_{i} \leq x \leq X_{i+1}\))での密度は
$$
y = Y_{i} \frac{X_{i+1} – x}{X_{i+1} – X_{i}} + Y_{i+1} \frac{X_{i} – x}{X_{i+1} – X_{i}}
$$
と計算されます。つまり、任意の点からその両側の2つのビンの中心座標までの距離に応じて配分(天秤算)されます。詳細は割愛しますが、2次元の場合はこれが任意とその点の周りの4つのビンの中心座標までの面積に応じて配分されることになります。
線形補間は密度の積分が保存することで正当性が担保される
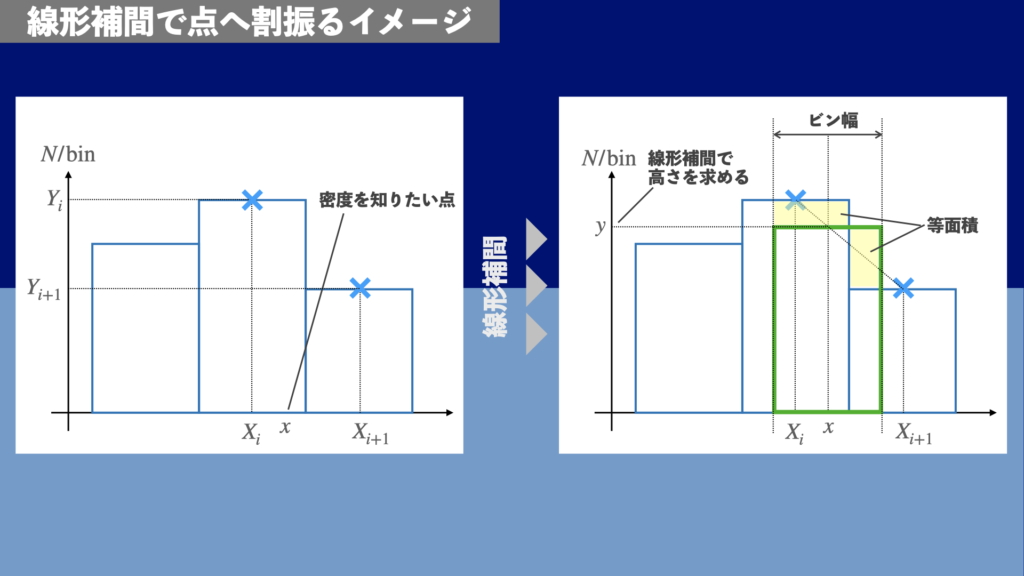
線形補間の利点は積分が保存するため、密度の補間方法として原理的な正しさが担保されることにあります。図8は線形補間の様子を図示したものです。図8の右側のように\(x\)の周りにビン幅分を仮定します。すると、このビン幅に含まれる元の密度(青い線の内部)を均すと緑の長方形の範囲になります。つまり図8右側の2つの黄色部分の面積は等しいです。このとき、緑の長方形の高さは\(Y_{i}\)と\(Y_{i+1}\)から線形補間したものと一致します。このように線形補間を行うことで、密度の積分、つまり点の数が保存します。
線形補間で点への割振りを行う密度カラープロットのパターン(方法2・方法5)
線形補間で点への割振りを行うパターンは図1の方法2、方法5に該当します。表5に方法2と方法5について、密度の計算、スムージング、点への割振りのパターンをまとめました。
| 方法2 | 方法5 | |
| 密度の計算 | ヒストグラム | ヒストグラム |
| スムージング | なし | 畳み込み |
| 点への割振り | 線形補間 | 線形補間 |
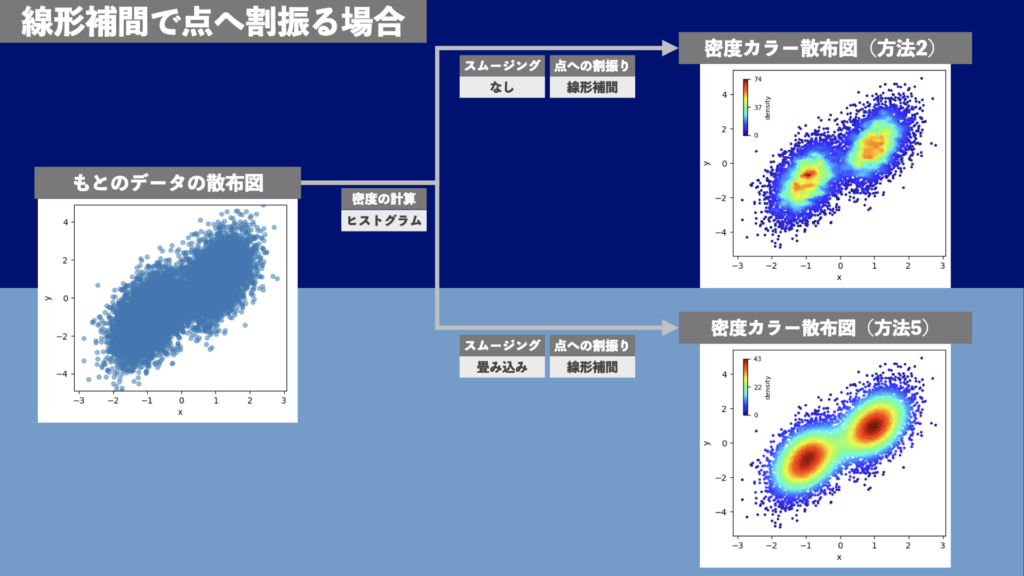
線形補間で点への割振りを行う密度カラープロットの例(方法2・方法5)
方法2と方法5で描画した例を図9に示します。データは図7と同じものです。点への割振りを行わなかった図7と比べると、点の密度が低い場所の様子もよくわかります。また、点の密度が高い場所もカラーで表示されるので様子がよくわかります。図9の右上と右下の違いはスムージングだけです。スムージングを行った右下のほうが、背景の双峰分布(正規分布2つ)をよく表していると言えそうです。
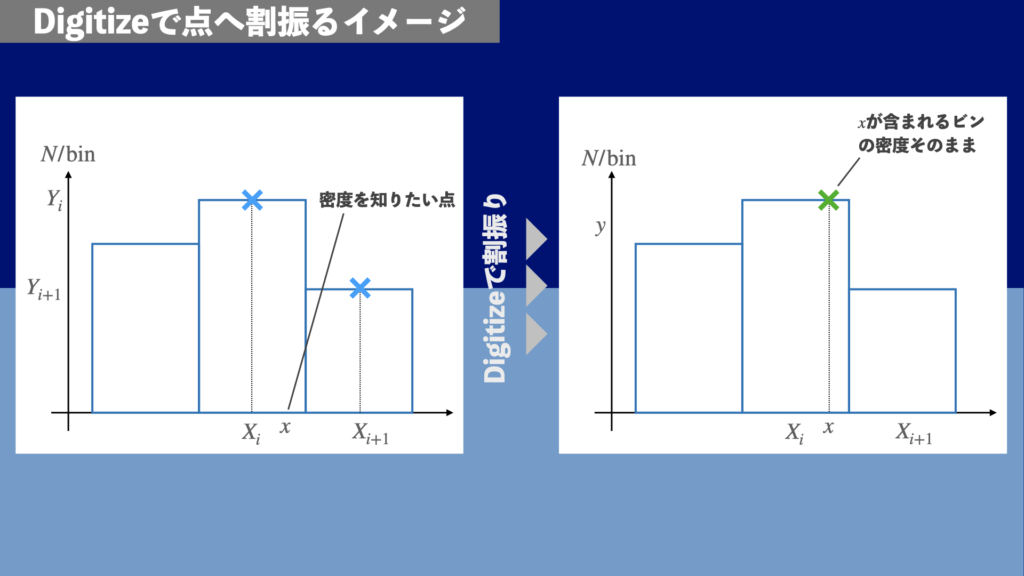
Digitizeで点への割振りを行う場合 | 方法3・方法6
Digitizeを使って、ヒストグラムで計算した密度をデータ点に割り振ることもできます。この方法は前述の線形補間とは異なり、補間を行いません。任意の点の密度は、その点が含まれるビンの密度となります。1次元の場合のイメージを図10に示します。元のヒストグラムの形がそのまま保存されるので、この方法でも原理的な正当性が担保されます。
Digitizeで点への割振りを行う密度カラープロットのパターン(方法3・方法6)
Digitizeで点への割振りを行うパターンは図1の方法3、方法6に該当します。表5に方法3と方法6について、密度の計算、スムージング、点への割振りのパターンをまとめました。
| 方法3 | 方法6 | |
| 密度の計算 | ヒストグラム | ヒストグラム |
| スムージング | なし | 畳み込み |
| 点への割振り | 線形補間 | 線形補間 |
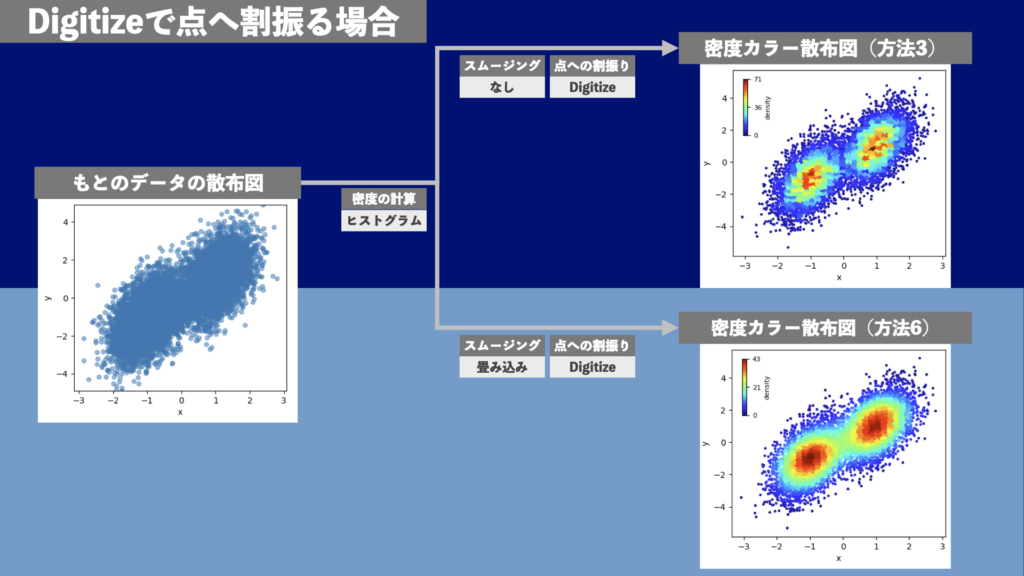
Digitizeで点への割振りを行う密度カラープロットの例(方法3・方法6)
方法3と方法6で描画描画した例を図11に示します。データは図7や図9と同じものです(ただし乱数が異なるため厳密には一致しません)。線形補間で点への割振りを行った図9と同様、点の密度が低い場所の様子も点の密度が高い場所の様子もよくわかります。図9と比べるとヒストグラムのビンの形が現れており、若干ガタガタする感じになります。
Result | 綺麗な散布図を描く方法8分類
綺麗な散布図すなわち密度カラー散布図を各方法は、ここまで解説した
- 密度の計算方法
- スムージング方法
- 点への割当方法
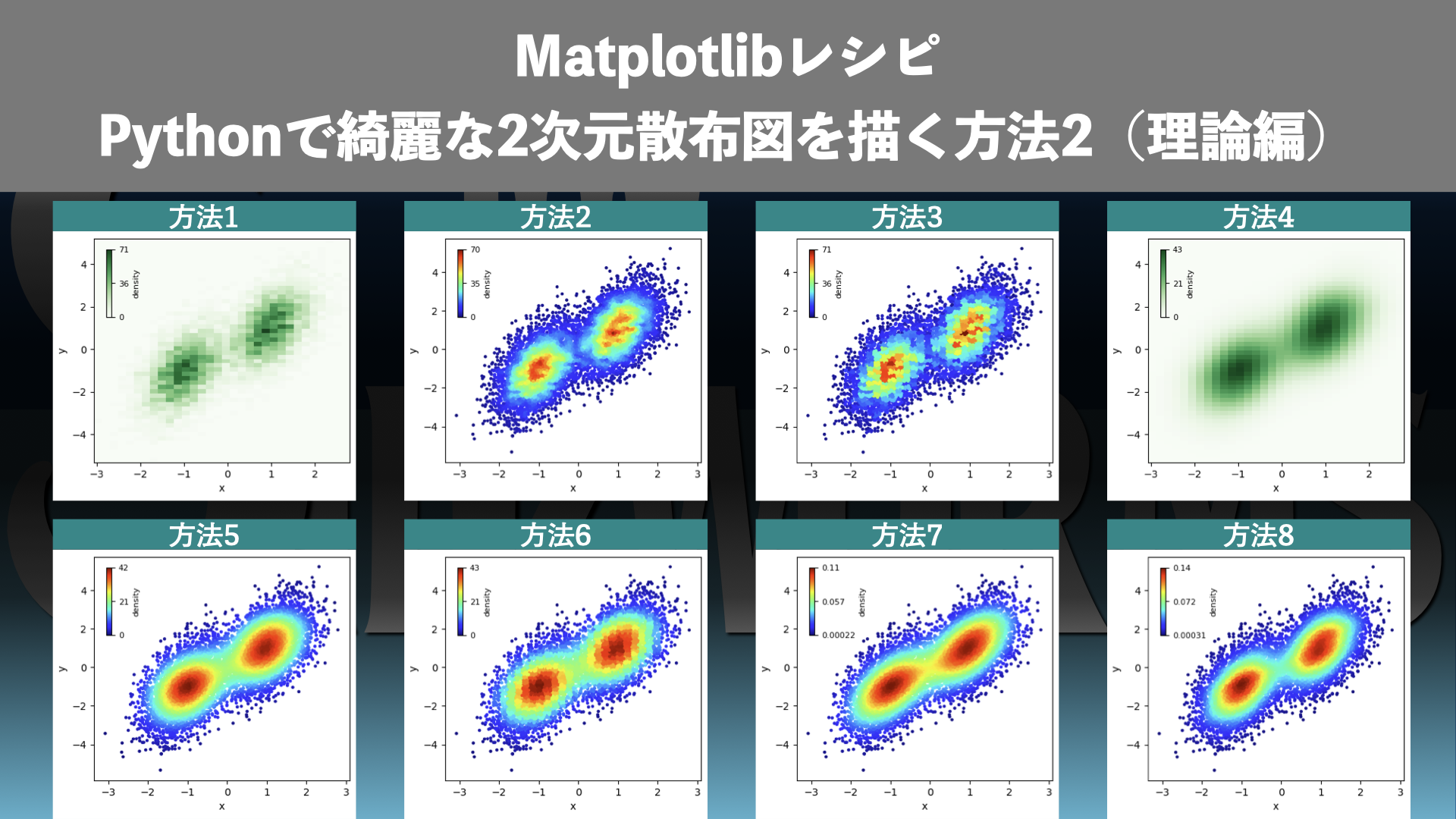
によって8つに分類できます。8つの方法を図12に再掲します(図1と同じもの)。

8つの方法による密度カラー散布図の描画例
密度カラー散布図を描く方法8分類で双峰分布を描画した例をまとめます。データは図7と同じ前回記事「Matplotlib | 綺麗な2次元散布図の描き方1(概要編)」の「データ2: 普通の散布図では様子がわかりにくい双峰分布の例」です。
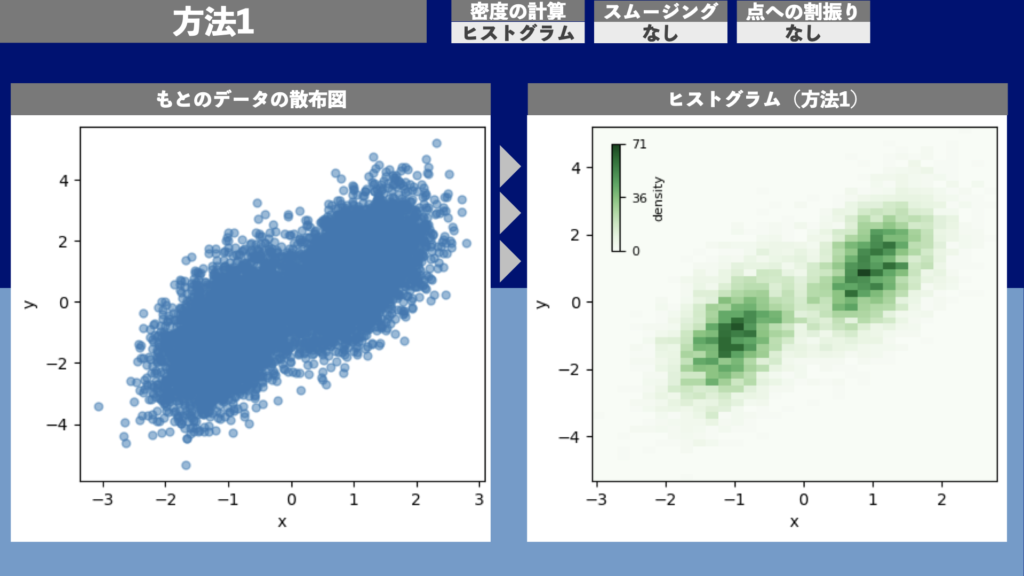
方法1 | 2次元ヒストグラム(密度計算: ヒストグラム、スムージング: なし、点への割振り: なし)
図13は方法1による2次元ヒストグラムの描画例です。1万点のデータ点について描画するのに約0.02秒の計算時間がかかりました。
方法2 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: なし、点への割振り: 線形補間)
図14は方法2による密度カラー散布図の描画例です。1万点のデータ点について描画するのに約0.02秒の計算時間がかかりました。
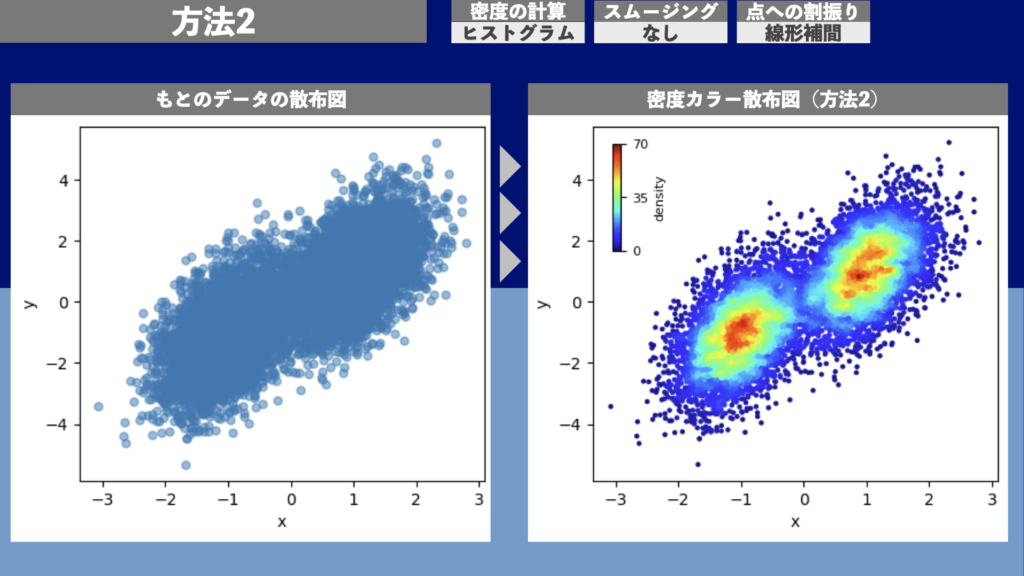
方法3 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: なし、点への割振り: Digitize)
図15は方法3による密度カラー散布図の描画例です。1万点のデータ点について描画するのに約0.02秒の計算時間がかかりました。
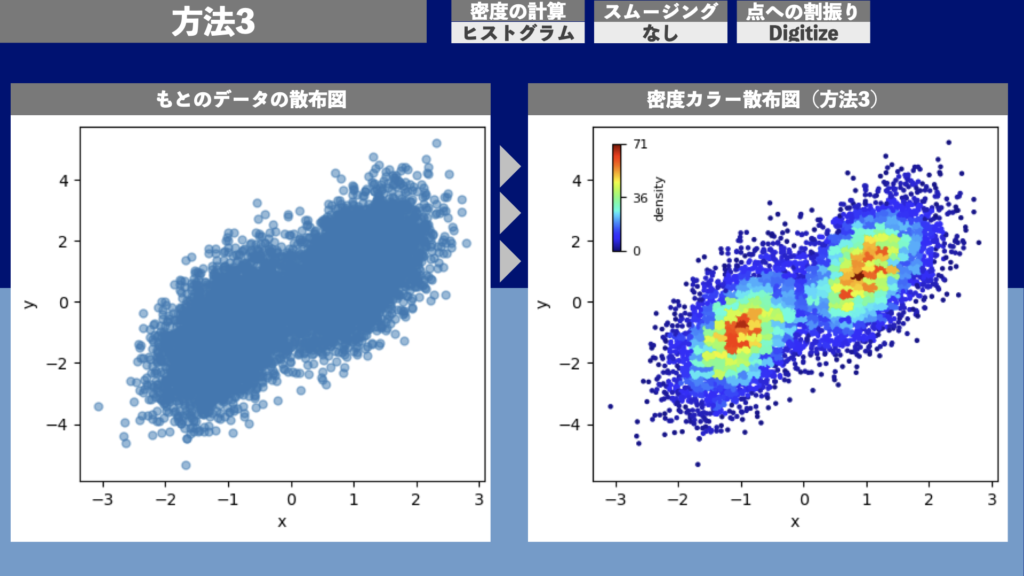
方法4 | 2次元ヒストグラム(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: なし)
図16は方法4による2次元ヒストグラムの描画例です。1万点のデータ点について描画するのに約0.02秒の計算時間がかかりました。
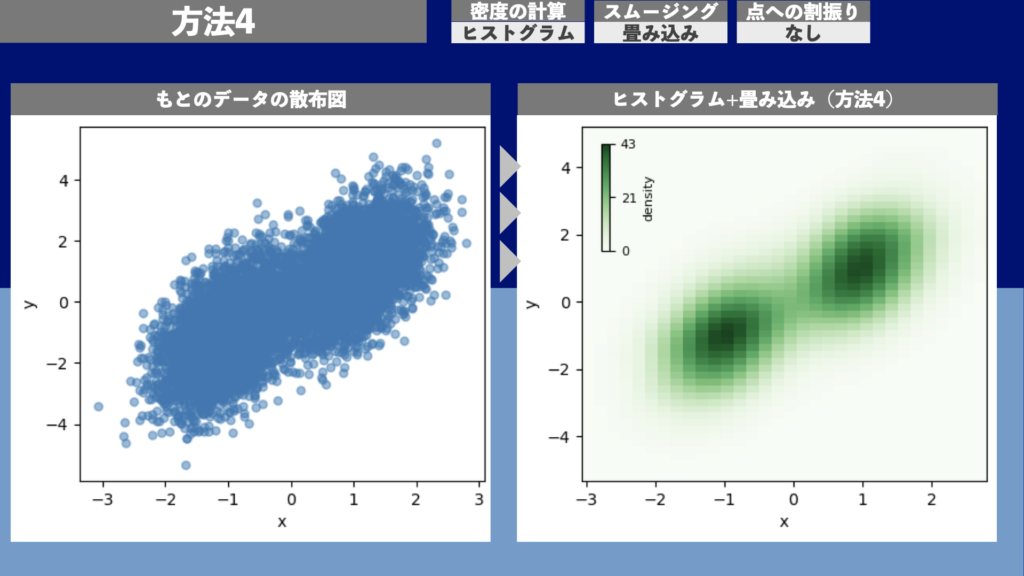
方法5 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: 線形補間)
図17は方法5による密度カラー散布図の描画例です。1万点のデータ点について描画するのに約0.02秒の計算時間がかかりました。
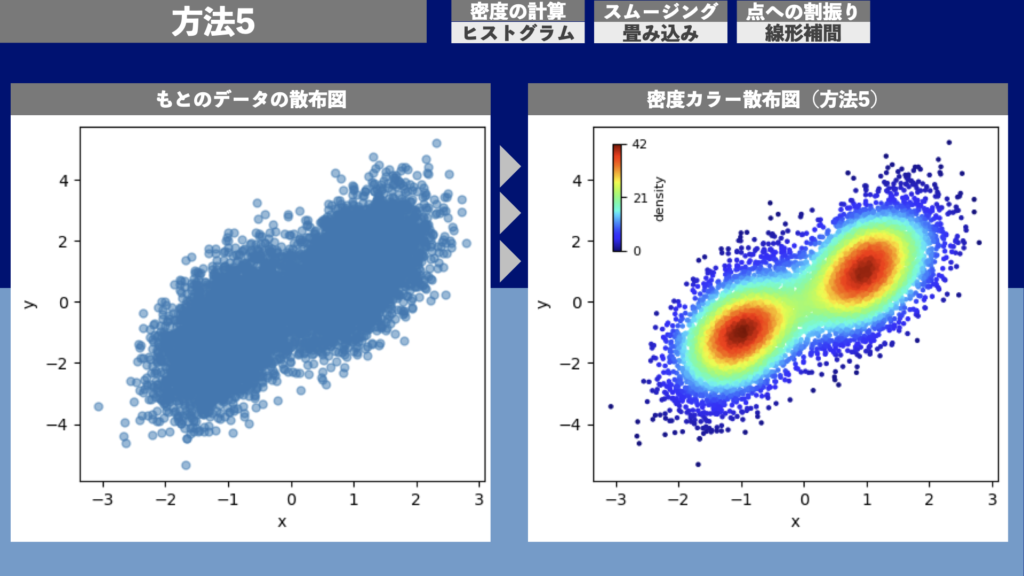
方法6 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: Digitize)
図18は方法6による密度カラー散布図の描画例です。1万点のデータ点について描画するのに約0.02秒の計算時間がかかりました。
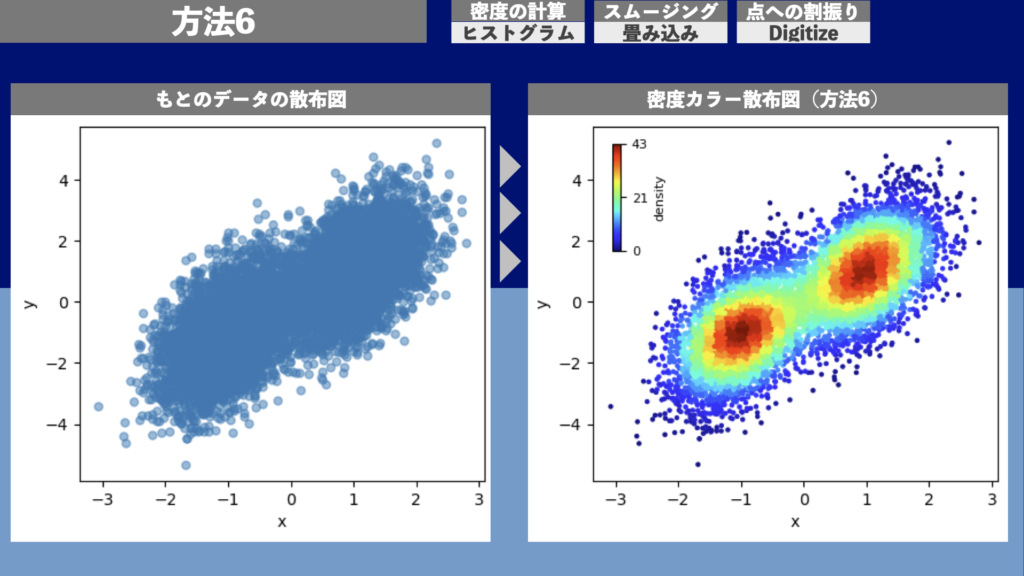
方法7 | 密度カラー散布図(密度計算: ヒストグラム、スムージング: KDE、点への割振り: N/A)
図19は方法7による密度カラー散布図の描画例です。1万点のデータ点について描画するのに約0.1秒の計算時間がかかりました。計算時間は方法1から方法6までの約50倍ということになります。
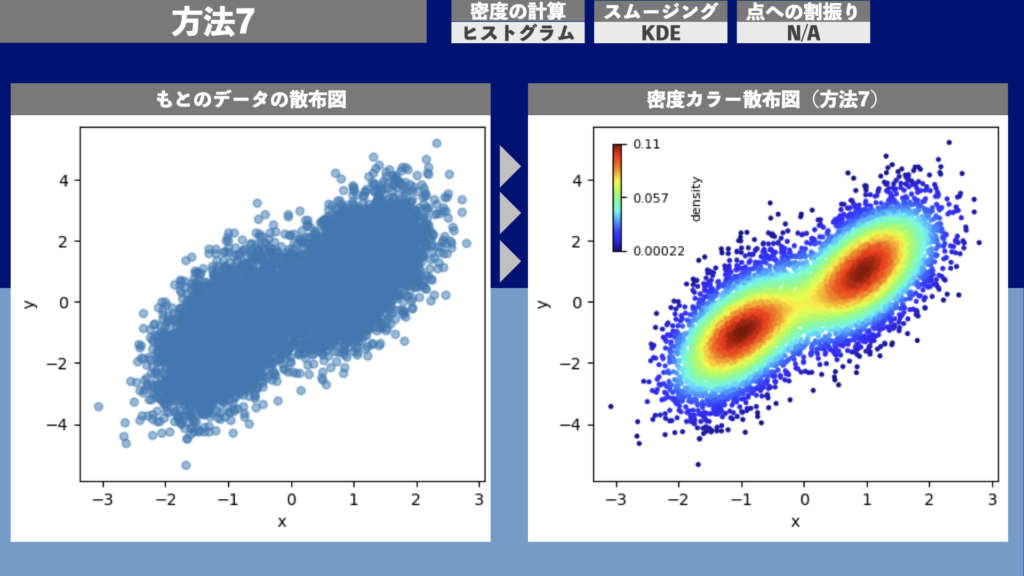
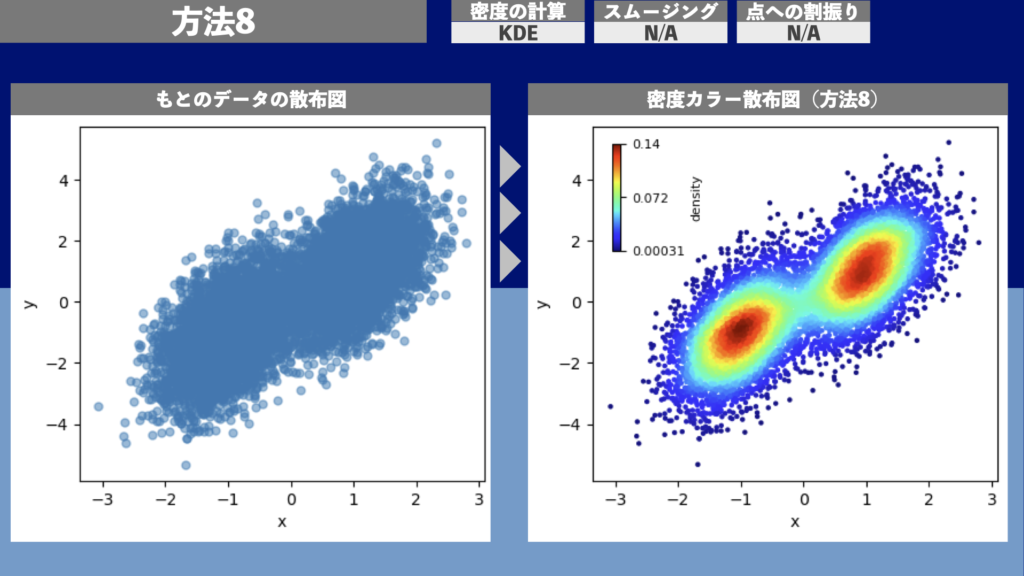
方法8 | 密度カラー散布図(密度計算: KDE、スムージング: N/A、点への割振り: N/A)
図20は方法8による密度カラー散布図の描画例です。1万点のデータ点について描画するのに約0.5秒の計算時間がかかりました。計算時間は方法7の5倍、方法1から方法6までの約250倍ということになります。
今回の図を作成したコードのサンプル
今回の図を作成したコードのサンプルを掲載します。それぞれの方法でプロットを作成するコードも含まれているので、ご利用ください!次回以降、それぞれの方法についてより実践的なコードを描いていくのでそちらもご期待ください!
Conclusion | まとめ
最後までご覧頂きありがとうございます!
Pythonで綺麗な散布図(=密度カラー散布図)を描く方法8分類をご紹介しました!
密度カラー散布図を描く方法は、
- 密度の計算方法
- スムージング方法
- 点への割振り方法
に着目することで8つに分類できます。基本的には、
- 方法5(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: 線形補間)
- 方法6(密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: Digitize)
あたりを使っておけば、計算速度も速く様々な場合に対応することができます。方法6の方が\(x\), \(y\)のヒストグラムビンのスケールが線形でない場合にも簡単に対応できるメリットがあります。状況に応じて使い分けても良いかもしれません。
以上「Matplotlib | Pythonで綺麗な2次元散布図を描く方法(2. 理論編)」でした!
またお会いしましょう!Ciao!
References | 参考文献と関連記事
今回の参考文献と本シリーズの関連記事もご覧ください。
参考文献
- カーネル密度推定: Wikipedia
- ノンパラメトリック密度推定(KDE): 東京大学の講義資料
- KDEのライブラリ: scipy.stats.gaussian_kde
本シリーズの関連記事
本シリーズ「Pythonで綺麗な2次元散布図を描く方法」の関連記事は以下です。 第1回の概要編に加え、密度カラー散布図の描き方の分類(2. 理論編)、基本的な実装方法(3. 基礎編)、1次元のヒストグラムと同時に描画する方法(4. 応用編)、軸のスケール設定を組み合わせる実装方法(5. 発展編)、任意の軸スケールで1次元ヒストグラムと同時に描画する方法(6.特別編)など詳しく扱っておりますので参考にどうぞ!
- Matplotlib | Pythonで綺麗な2次元散布図を描く方法(1. 概要編)
- Matplotlib | Pythonで綺麗な2次元散布図を描く方法(2. 理論編)
- Matplotlib | Pythonで綺麗な2次元散布図の実装方法(3. 基礎編)
- Matplotlib | Pythonで散布図を1次元ヒストグラムと同時にプロットする方法(4. 応用編)
- Matplotlib | 任意の軸スケールで密度カラー散布図をプロットする方法(Python散布図 5. 発展編)
- Matplotlib | 密度カラー散布図を任意の軸スケールで1次元ヒストグラムと同時にプロットする方法(Python散布図 6. 特別編)

コメント