Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信していきます。
今回はpythonデータ解析編、知っていると便利な確率分布、JohnsonのSU分布の第2回、基礎編です!
基礎編では、JohnsonのSU分布の確率密度関数、そのパラメータを変化させると分布の形がどう変わるかなどの性質をご紹介します。
第1回の導入編ではJohnsonのSU分布が必要になる現実のデータの例をご紹介しました。
まだ導入編を見ていない方は、ぜひそちらも御覧ください!
導入編: https://the-silkworms.com/ds_stat_johnsons-su_intro/94/
Abstract | JohnsonのSU分布は正規分布 + 非対称性 + 裾野調整
JohnsonのSU分布は、正規分布に非対称性と裾野を調整するパラメータを追加したものです。
正規分布は中心位置と全体の広がりを調整する2つのパラメータで制御しますので、SU分布ではこれに2つパラメータを足して、4パラメータで分布を制御することになります。
JohnsonのSU分布の定式は以下のようになります。
$$f(x, \gamma, \xi, \delta, \lambda) = \frac{\delta}{\sqrt{1 + \left(\frac{x – \xi}{\lambda}\right)^{2}}} \phi \left(\gamma + \delta \sinh^{-1} \left( \frac{x – \xi}{\lambda} \right) \right) \tag{4}$$
ここで、\(\phi\)は正規分布の確率密度関数です。
かなり複雑な式ですが、4つのパラメータの役割
- \(\xi\): 分布の左右位置を決定する
- \(\lambda\): 分布の全体的な広がりを決定する
- \(\gamma\): 分布の左右非対称性(歪度)を決定する
- \(\delta\): 分布の裾野の広がり(尖度)を決定する
を頭に入れておけば、JohsonのSU分布を使いこなすことができます!
Method | JohnsonのSU分布の関数形(読み飛ばしてくださいw)
JohnsonのSU分布は、1949年にNorman Lloyd Johnson教授が正規分布の変数変換として考案したものです。
JohnsonのSU分布の関数形は複雑なので、
- 正規分布の変数変換
- 4つのパラメータをもつ
ということと、4つのパラメータは分布の
- 左右の位置を決定する
- 全体的な広がりを決定する
- 左右非対称性(歪度)を決定する
- 裾野の広がり(尖度)を決定する
ことを頭に入れておきましょう。
一応、以下に関数形を紹介しておきます。
実用上はpythonの科学計算ライブラリscipyで計算できてしまうので、複雑な式を覚える必要はありません。
SU分布の確率密度関数の関数形
JohnsonのSU分布の確率分布関数は以下のように定式化されます。
$$f(x, \gamma, \xi, \delta, \lambda) = \frac{\delta}{\lambda \sqrt{2 \pi}} \frac{1}{\sqrt{1 + \left(\frac{x – \xi}{\lambda}\right)^{2}}} \exp \left[-\frac{1}{2} \left( \gamma + \delta \sinh^{-1} \left( \frac{x – \xi}{\lambda} \right) \right)^{2} \right] \tag{1}$$
\(\gamma, \xi, \delta>0, \lambda>0\)はSU分布の4つのパラメータです。「ガンマ、グザイ、デルタ、ラムダ」と読みます。
また、 \(\sinh^{-1}\)は双曲線関数\(\sinh\)(ハイパボリックサイン)の逆関数で
$$\sinh^{-1}(x) = \log(x + \sqrt{x^2+1} ) \tag{2}$$
です。
逆関数を取る前の、\(\sinh\)関数は
$$ \sinh(x) = \frac{\exp(x) – \exp(-x)}{2} \tag{3}$$
です。
式(1)を変換すると、以下の形になります(詳細割愛)。
$$f(x, \gamma, \xi, \delta, \lambda) = \frac{\delta}{\sqrt{1 + \left(\frac{x – \xi}{\lambda}\right)^{2}}} \phi \left(\gamma + \delta \sinh^{-1} \left( \frac{x – \xi}{\lambda} \right) \right) \tag{4}$$
ここで、\(\phi\)は正規分布の確率密度関数です。「ファイ」と読みます。
かなり複雑な式ですが、正規分布が変数変換された形になっていることがわかります。
式を覚えたり、完全に理解する必要はありません。
しかし、\(\gamma, \delta, \xi, \lambda\)の4つのパラメータの以下の役割は抑えておきましょう。
このあと、図を使って分布の形状を眺めると理解が深まるはずです。
- \(\xi\): 分布の左右位置を決定する
- \(\lambda\): 分布の全体的な広がりを決定する
- \(\gamma\): 分布の左右非対称性(歪度)を決定する
- \(\delta\): 分布の裾野の広がり(尖度)を決定する
SU分布の累積分布関数の関数形
累積分布関数は
$$ \Phi\left( \gamma + \delta \sinh^{-1}\left( \frac{x – \xi}{\lambda} \right) \right) \tag{5}$$
と表されます。
ここで、\( \Phi \)は標準正規分布の累積分布関数です。こちらは大文字の「ファイ」です。
SU分布の平均値・中央値・分散
平均値は
$$\mu = \xi – \lambda \exp \left( \frac{\delta^{-2}}{2} \right) \sinh \left( \frac{\gamma}{\delta} \right) \tag{6}$$
となります。\(\mu\)は「ミュー」と読みます。
\(\gamma = 0\)、つまり左右非対称性がないとき、\(\sinh\)の項が0なので、平均値は正規分布の平均値に相当するパラメータ\(\xi\)と一致します。
逆に\(\gamma \neq 0\)、つまり左右非対称性のときには、\(\xi\)が平均値となるわけではなく、SU分布の平均値は\(\xi\)からずれることに注意が必要です。
中央値は
$$\nu = \xi + \lambda \sinh \left( – \frac{\gamma}{\delta} \right) \tag{7}$$
で与えられます。\(\nu\)は「ニュー」と読みます。
\(\gamma = 0\)のとき、平均値と一致し\(\xi\)とも一致します。
\(\gamma\)がゼロでないときには、平均値や\(\xi\)からずれます。
分散は
$$\sigma^{2} = \frac{\lambda^{2}}{2} \left( \exp\left( \delta^{2} \right) -1 \right) \left( \exp \left( \delta^{2} \right) \cosh \left( \frac{2 \gamma}{\delta} \right) +1 \right) \tag{8}$$
で与えられます。
正規分布の分散に相当する\(\lambda^{2}\)とは一致しません。
\(\lambda^{2}\)からのズレの程度は歪度と尖度に依存します。
ちなみに式(8)の\(\cosh\)は双曲線関数ハイパボリックコサインで、
$$ \cosh(x) = \frac{\exp(x) + \exp(-x)}{2} $$
と表されます。
上記の他に、分布の形状を表す特徴量である尖度や歪度も定式化することができます。
これらは、\(\gamma\)と\(\delta\)が組み合わさった式で表されますが、\(\xi\)と\(\lambda\)は現れません。
つまり、尖度と歪度は分布の中心位置(\(\xi\))や全体的な広がり(\(\lambda\))には依存しません。
尖度と歪度の式はここでは紹介しませんが、気になる方は調べてみてください。
参考になるウェブページを最後に紹介します!
Result | JohnsonのSU分布を眺めてみよう!
複雑な数式を完全に理解する必要はありませんが、どのパラメータを動かすと分布の形状がどのように変化するのかを知っておくことは、実用する上で役に立ちます。
実際にJohnsonのSU分布のパラメータを変えてみてして、非対称性や裾野がどのように変化するか、形状を確かめてみましょう!
分布の左右位置と全体的な広がりを決定する\(\xi, \lambda\)は、非対称性と裾野には無関係なので、それぞれ0と1で固定します(正規分布で言えば標準正規分布)。
非対称性を入れない場合 | 非対称性のパラメータ(\(\gamma = 0\))
まず、非対称性を入れない、すなわち\(\gamma=0\)の場合の分布形状を見てみましょう。
裾野を調整するパラメータ\(\delta\)を変化させます。
\(\delta\)を変化させることで裾野の広がり方が変わることを確認してください。
裾野を調整するパラメータ\(\delta = 1\)の場合
\(\delta=1\)のときの、Johnson SU分布(赤実線)と比較用に正規分布(シアン点線)を以下にプロットします。
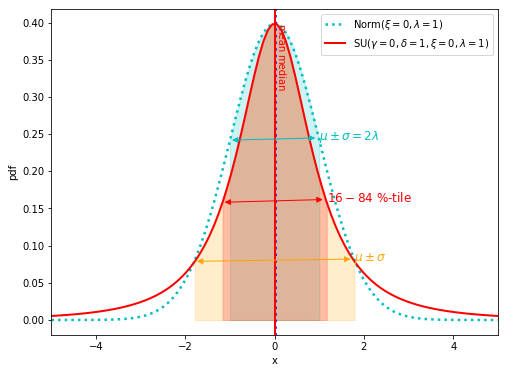
正規分布に比べて、裾野が広がっています。
そのため、分散を比較するとSU分布の方が大きいです。
これは、正規分布の標準偏差の範囲(シアン矢印)とSU分布の標準偏差の範囲(オレンジ矢印)を比較するとわかります。
オレンジ矢印の方がだいぶ長いですよね。
また、ピークの値が正規分布とSU分布とで一致していることにも注目しましょう。
裾野を調整するパラメータを増やした場合\(\delta = 2\)
\(\delta=2\)に増加させると、ピークが高く、裾野の狭い分布になります。
Johnson SU分布(赤実線)と正規分布(シアン点線)のプロットを御覧ください。
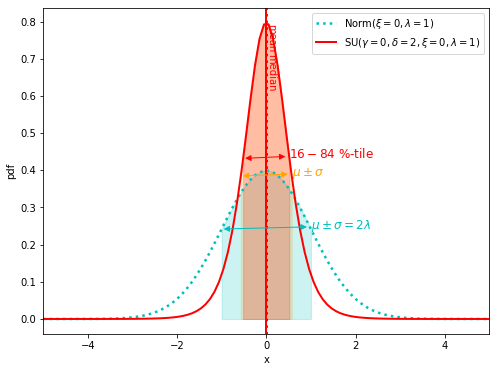
\(\delta = 1\)のときと比べて、鋭く尖っており、分散も小さいです。
また、標準偏差2つ分(2\(\sigma\))の範囲(オレンジ矢印)と16 %-tileから84 %-tileの範囲(赤矢印)が近づいています。
これは裾野が狭くなっている(あるいは薄くなっている)ことを意味します。
裾野を調整するパラメータを減らした場合\(\delta = 0.5\)
\(\delta=0.5\)に減少させると、ピークが低く、裾野の広がった分布になります。
Johnson SU分布(赤実線)と正規分布(シアン点線)のプロットを御覧ください。
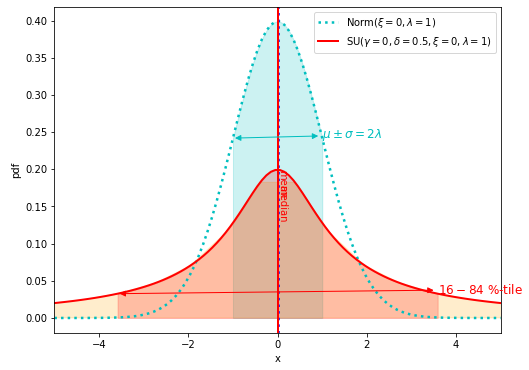
\(\delta = 1\)のときと比べて、なまった形になっており、分散も大きいです。
また、標準偏差2つ分(2\(\sigma\))の範囲(オレンジ矢印)と16 %-tileから84 %-tileの範囲(オレンジの塗色範囲で画面外まではみ出ている)の乖離が大きくなっています。
これは裾野が広くなっている(あるいは暑くなっている)ことを意味します。
非対称性を入れる場合 | 非対称性のパラメータ(\(\gamma \neq 0\))
今度は\(\gamma\)を変化させることで、分布の左右非対称性が変化することを確認しましょう!
\(\gamma = 1\)の場合
\(\gamma=1\)のとき、Johnson SU分布は左側に偏ります。
Johnson SU分布(赤実線)と比較用に正規分布(シアン点線)を以下にプロットします。
ここでは\(\delta\)は1に固定します。
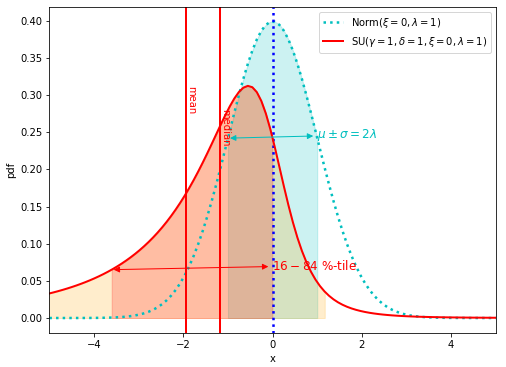
非対称性がないときと比べて、左側に偏った分布となっています。
ピークや平均、中央値も左側に偏ります。
また、ピークが小さく、裾野が広がった分布になっています。
標準偏差2つ分(2\(\sigma\))の範囲(オレンジ矢印)と16 %-tileから84 %-tileの範囲(オレンジの塗色範囲で画面外まではみ出ている)の乖離が大きくなっていることからも、裾野が広がっていることがわかります。
\(\gamma = -1\)の場合
\(\gamma=-1\)のとき、Johnson SU分布は右側に偏ります。
Johnson SU分布(赤実線)と比較用に正規分布(シアン点線)を以下にプロットします。
ここでも\(\delta\)は1に固定します。
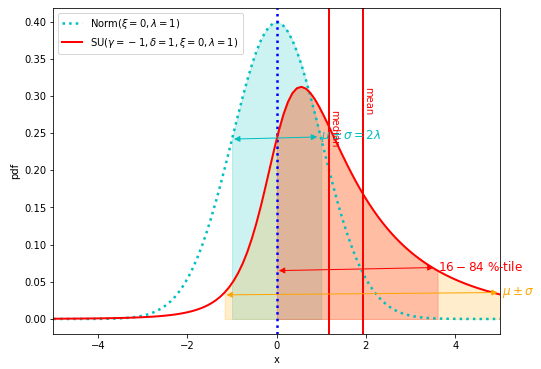
非対称性がないときと比べて、右側に偏った分布となっています。
ピークや平均、中央値も右側に偏ります。
裾野が広がり具合は\(\gamma = 1\)のときと同じです。
\(\gamma = -1\)で裾野パラメータ\(\delta\)を増加させた場合
最後に、\(\gamma=-1\)のまま、\(\delta=2\)に増やしてみましょう。
Johnson SU分布のピークは右側に偏っているものの、平均値や中央値の偏りは少なくなります。
Johnson SU分布(赤実線)と比較用に正規分布(シアン点線)を以下にプロットします。
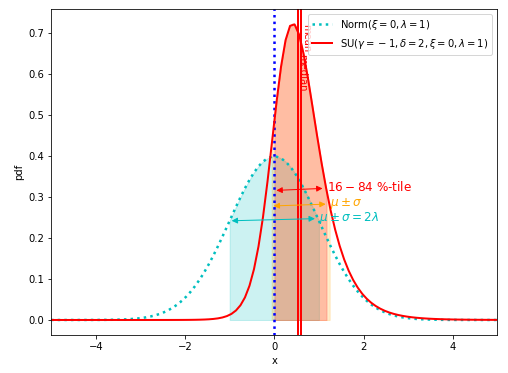
裾野調整パラメータ\(\delta\)が小さいときと比べて、平均、中央値の偏りが小さくなります。
\(\delta\)を大きくすると裾野が狭くなるため、右側に偏って広がっていた裾野の影響が小さくなるためです。
Conclusion | 基礎編のまとめ
JohnsonのSU分布の第2回基礎編、最後まで読んでいただきありがとうございます!
式で見るととても複雑に見えますが、JohnsonのSU分布の解釈は単純です。
正規分布に歪度(非対称性)と尖度(裾野の具合)が加わっているだけです。
4つのパラメータの以下の役割、
- \(\xi\): 分布の左右位置を決定する
- \(\lambda\): 分布の全体的な広がりを決定する
- \(\gamma\): 分布の左右非対称性(歪度)を決定する
- \(\delta\): 分布の裾野の広がり(尖度)を決定する
とそれぞれのパラメータを変化させたときの分布形状の変化を頭に入れておけば、実用上問題なくJohnsonのSU分布を使いこなせるはずです!
以上、「統計学レシピ|正規分布を超えたいあなたに捧げるJohnsonのSU分布(基礎編)」でした!
次回の実践編ではpythonを使って、JohnsonのSU分布の作図例や、実際のデータへのフィット例をご紹介します!
お楽しみに!Ciao!
References | 参考
Wikipedia (英語版のみ): https://en.wikipedia.org/wiki/Johnson’s_SU-distribution
よくまとまったExcellアドインのサイト: http://www.ntrand.com/jp/johnson-su-distribution/
scipyのマニュアル: https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.johnsonsu.html
コメント
式(4)の、φの前のδは不要じゃないでしょうか。
コメントありがとうございます!
恐らく式(4)の最初のδは必要です。式(1)の最初のδが残るかと思います。
また、x-ξ=0のとき確率密度関数(PDF)が最大となりますが、最大値がδによって変化するはずです。最初のδがない場合、尖度によらずPDFの最大値が一定になってしまうので直感と反すると思います。x-ξ=0のとき、sinh^{-1}(0) = log(1) = 0となるので、標準正規分布の密度関数φ部分(φ(λ))はδに依存しなくなるためです。
なんか材料物理数学再武装で有名なクボタメソッドでは確率密度関数の対称、非対称に成分を分けてそれぞれの情報からもともとの正規分布がどのような曲線を経ているかを解析する手法があったな。