Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
今回は統計学&pythonレシピです!
本シリーズでは、任意の確率分布から任意の個数のランダムサンプルを得る方法をご紹介しています!
第4回の今回は本シリーズ最終回となります!
これまでのシリーズ第2回(前々回)と第3回(前回)では、そのための2つの手法
- 棄却サンプリング (rejection sampling)
- MHサンプリング (Metropolis-Hastings sampling)
のご紹介しました。
シリーズ第1回では、任意の確率分布からのサンプリングが必要になる例をご紹介しました。
シリーズ第4回の今回は、棄却サンプリングをnumpyで高速実装する方法をご紹介します!
棄却サンプリングはマルコフ連鎖を使わない単純かつ直感的なサンプリング方法です。
マルコフ連鎖を使わない(すなわち再帰的な処理が不要)ため、numpyによる実装が簡単にできます。
第2回でのnumpyを使わない実装方法では、loop処理を行うため多大な計算時間が必要でした。
numpy等の高速ライブラリを利用し、python高速実装のポイントは明示的なloop処理を書かないことです。
numpyを使う今回の方法では、計算時間は第2回の方法の1/100近くまで短縮されます!
今回は、「棄却サンプリングが便利なことはわかった。でも流石に計算時間がかかりすぎるからなんとかしたい!」というみなさんのお悩みを解決します!
ぜひ最後までお付き合いください!
Abstract | NumPyでループ処理を避けて高速棄却サンプリング!
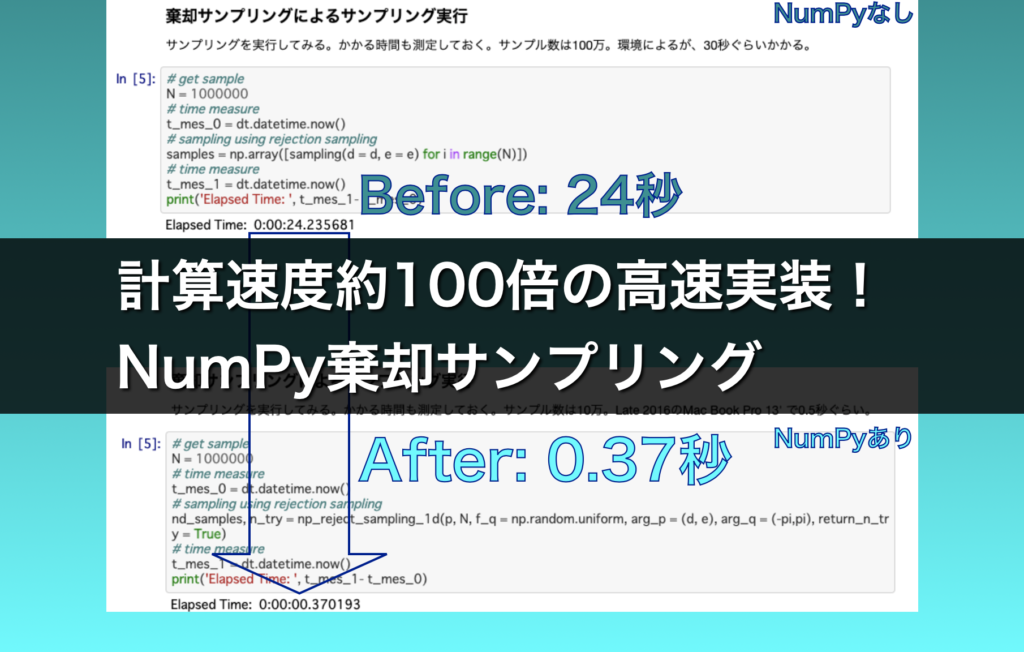
第2回でご紹介した棄却サンプリングの実装方法は、100万サンプル得るのに私の環境で30秒近く時間がかかる遅いものでした。
計算時間がかかってしまう理由は、ループ処理を行っているためです。
pythonのループ処理(forループやwhileループ)は、C言語などコンパイル言語と比べて時間がかかることが知られています。
NumPyライブラリは、pythonの計算時間を短縮するための強力な手法です。
NumPyライブラリは裏側でC言語のプログラムが動いているため、計算が高速です。
また、ループ処理をコード上に書く必要がなく、コードの見た目もスッキリします。
今回は、NumPyを使って棄却サンプリングを実装する方法をご紹介します。
この方法では100万サンプル得るのにかかる時間は、私の環境では0.5秒以下となりました。
NumPyを使わない方法と比べて1/100近くに短縮されたことになります。
NumPyによる実装方法をマスターして高速な棄却サンプリングを使っていきましょう!
Background | pythonのループ処理は遅い
pythonのループ処理は遅いです。これはpythonだけでなく、Rなどのいわゆるインタプリタ言語に共通する特徴です。
何に比べて遅いかというと、FortranやCなどのいわゆるコンパイル言語に比べて遅いことが知られています。
pythonのループ処理が遅い要因は主に以下の2つのようです。
- インタプリタ言語だから
- 動的な型変換を行うから
コンパイル言語に比べてインタプリタ言語のループ処理が早いのは、コーディングと実行の間にコンパイル作業を挟むことで、計算機の動作に最適化された形に翻訳されるためです。
コンパイルとは、人間が読める言語で書かれたコードを計算機が読める機械語に翻訳する作業です。
FortranやCと言った言語は、
- コーディング
- コンパイル
- 実行
という手順を踏みます。
一方、pythonやRなどのインタプリタ言語は、コンパイル作業を間にはさみません。
コーディングから実行まで段階が一つ少ないので手軽です。
しかし、計算機の動作に最適化された形に翻訳されない状態で実行が行われるので、複雑な処理を行うときにどうしても処理が遅くなります。
また、pythonでは動的な型変換を行いながら処理が行われるようです。
例えばある変数aに値を代入する際には、float型かint型か等々のチェックがいちいち行われるために処理に時間がかかります。
C言語の場合には最初に型の宣言をして、そのとおりの型を代入しないとコンパイルでエラーになります。
pythonではコンパイルを省いている分、実行時にしわ寄せが来ていると考えることができます。
型変換が動的であるということは、参照するメモリ領域がいちいち変わる可能性があるということです。
メモリとはコンピュータ上の一時記憶領域、作業台のようなものです。
配列などを宣言すると、この領域上に配列のデータ置き場が作られます。
ループ処理で配列を参照するには際、メモリが「整然と並んでいる」方が高速に処理されます。
n個の要素のベクトルならば、n個が一列に並んでいる状態の方が処理が早いのです。
C言語で配列を宣言する場合、mallocなどの関数でメモリを割り当てますが、配列はメモリ上に「整然と」確保されます。
一方、pythonで、例えばリストを定義した際には、メモリ上の空いているところに割り当てられます。
ループ処理で、いろいろなところに散らばったメモリを参照しようとすると、時間がかかるわけです。
このような理由で、pythonのループ処理はC言語等に比べて遅いのです。
Contents | NumPyによる棄却サンプリングの高速実装
NumPyを使って棄却サンプリングを高速実装する方法をご紹介します!
NumPyによる高速化の概要
pythonのループ処理を高速化する強力な手法の一つが、NumPyの配列を使うことです。
NumPyは背後でCのプログラムが動いているため、配列の繰り返し計算を高速に行うことができます。
しかも、配列の繰り返し計算を行う際に、forループやwhileループを明示的に書く必要がないため、コードの見た目もスッキリします。ただ、NumPyの書き方に慣れていないとどんな処理をしているか全くわからないかもしれません。
第2回で紹介した棄却サンプリングの実装では、複数のランダムサンプルを得るための繰り返し処理にNumPyを使わず、whileループを使っていました。
100万個のサンプルを得るのに30秒近くかかっていましたが、このような繰り返し処理は工夫するとNumPyで実装できます。
NumPyを使って繰り返し処理を高速化するには、予め定義された配列に対して同じ処理をさせることで、forループを書かないようにする必要があります。
棄却サンプリングでは、すべての候補点\(x_{i}\)の配列を予め用意します。
これは棄却される分も含めて用意します。
結局は使われない分まで配列を定義する必要があるため、メモリの無駄遣いといえば無駄遣いですが、その分CPUの処理時間を節約することになります。
NumPyで繰り返し処理を高速化するコツは、メモリを使ってCPUを節約することです。
NumPyによる棄却サンプリングの実装例
ソースコードは以下です。
コピー&ペーストして使っていただいて構いません。自己責任でご利用ください。
matplotlibはversion3.3.4が必要です(それ以前はhistogramにdensityパラメータがない)。
↓スクロールしてご覧ください。
ソースコードの最後に書いてあるとおり、100万サンプル得るのに0.5秒かからないぐらいです。
第2回で紹介した方法と比べて1/100近くまで計算時間が短縮されます。
コーディングのポイント
コーディングのポイントを解説します。
かなり細かいので読み飛ばして構いません。
上のコードをご利用の際に、参考にしていただけるようにポイントを書いておきます。
1変数棄却サンプリング関数
棄却サンプリングは「np_reject_sampling_1d」という関数で、以下の箇所に実装されています。
この関数は1変数であれば、様々な目標分布を提案分布を受け入れることができるようにしてあります。
# numpy rejection sampling
def np_reject_sampling_1d(f_p, N, f_q = np.random.uniform, arg_p = None, arg_q = None, N0 = 1000, N_factor = 2.0, return_n_try = False):
##############################################
# arguments:
# f_p <object>: function proportional to probability density function
# N: sample size
# f_q <object> : function for proposal distribution
# arg_p <tuple>: arguments passed to f_p other
# arg_q <tuple>: arguments passed to f_q other than the "size" argument
# N0 <int>: tentative sample size to estimate acceptance rate (r_a)
# N_factor <float> : tentative sample size will be 1/r_a * N_factor
# return_ntry <bool> : If try number of trial for sample generation is returned
# return:
# 1d array with size N
##############################################コードのコメントにも書いてありますが、主な引数は以下のとおりです。
- f_p: 目標分布\(P(x)\)を与える関数
- N: 所望のランダムサンプルのサイズ(\N\)
- f_q: 提案分布\(Q(x)\)を与える関数
- arg_p: 目標分布\(P(x)\)の変数\(x\)とサンプルサイズ\(N\)以外で、f_pに渡す引数
- arg_q: サンプルサイズ\(N\)以外で提案分布\(Q(x)\)に渡す引数
上記以外の引数(N0, N_factor, return_ntry)はとりあえず無視して構いません。
np_reject_sampling_1d()を呼び出す際には、f_pとf_qは別途定義された関数を渡します。
f_qはnp.random.uniform()のように、サンプル数を引数に取る関数であり、NumPy配列(numpy array)を返す関数である必要があります。
np.random.uniform()は、第1引数、第2引数に最大値と最小値を、最後の引数にサンプル数を受け付けます。
f_qに渡す引数は、arg_qとサンプル数です。
arg_qはタプルで、サンプル数以外の引数をタプルにして渡します。
arg_q、サンプル数の順番で渡すので、f_qにはサンプル数が最後の引数として渡される必要があります。
Nサンプル採択されるための候補点数の決定
np_reject_sampling_1d()内の以下の箇所では、予め用意する候補点の数を決めています。
# - get acceptance rate - #
x = f_q(*arg_q, N0)
## get unnormalized probability
p_x = f_p(x, *arg_p)
## get k factor which makes k * f_q(x) > f_p(x) for all x.
k = np.max(p_x)
## get sampling from [0, k * f_q(x)]
u = k * np.random.uniform(0, 1.0, N0)
## get acceptance rate
r_a = float(len(np.where((p_x > u))[0])) / float(N0)
# - define tentative sample size - #
Nt = int(N / r_a * N_factor)NumPyを用いた実装では、候補点を一つ一つ抽出し採択か棄却かを決定するということはしません。
すなわち、前もって棄却される点も含めて配列に格納しておく必要があります。
したがって、予め、どのくらいの候補点を用意しておけば所望の\(N\)個のランダムサンプルが得られるのか調べておく必要があります。
まずは採択率(acceptance rate)を調べます。
採択率が高ければ、\(N\)個のランダムサンプルを得るための候補点の数は\(N\)に近い値になり、低ければ\(N\)よりも沢山の候補点を用意する必要があるということです。
採択率の測定には、N0個の候補点を試しに提案分布から抽出して使います。
np_reject_sampling_1d()の引数N0は、この測定のために使う候補点の数です。\(N\)よりも小さいことが想定されます。デフォルトでは1000です。
測定された採択率は、r_aという変数に格納されています。
用意する候補点の数はNtという変数に格納されます。
所望のランダムサンプル数\(N\)をr_aで割った数にN_factorという値を乗じた数がNtです。
採択率がr_aなので、\(N\)個の採択を得るには\(N\)/r_a程度の候補点があれば良いはずです。
ただしr_aの測定にもばらつきがあるので、あまりぎりぎりだと\(N\)個の採択が得られない可能性もあります。
それを防ぐために、N_factorを余裕をもたせるための係数として入れています。デフォルトでは2となっています。
棄却サンプリングのNumPy実装部分
棄却サンプリングがNumPy実装されているのは以下の箇所です。
# - prepare array to return - #
ary_sample = np.zeros([0])
N_current = 0
# - loop until sampling number exceeds N - #
n_try = 0
while (N_current < N):
# - get sample - #
x = f_q(*arg_q, Nt)
## get unnormalized probability
p_x = f_p(x, *arg_p)
## get k factor which makes k * f_q(x) > f_p(x) for all x.
k = np.max(p_x)
## get sampling from [0, k * f_q(x)]
u = k * np.random.uniform(0, 1.0, Nt)
## select x whose p_x exceeds u and append to returned array
tmp_sample = x[ np.where(p_x > u) ]
ary_sample = np.r_[ ary_sample, tmp_sample ]
## length of the selected array
N_current = len(ary_sample)
## increment for n_try
n_try += 1
# - adjust array size - #
ary_sample = ary_sample[:N]このwhileループがサンプル数に対して回っていないことがポイントです。
ループの回数はたいてい1回で済みます。
whileループの中では以下のような処理をしています。
- Nt個の候補点を提案分布から抽出する: x = f_q(*arg_q, Nt)
- 全ての候補点の目標分布関数の値を計算する: p_x = f_p(x, *arg_p)
- 提案分布が目標分布を覆えるための係数kを決める: k = np.max(p_x)
- \(k \times Q(x)\)の一様分布を得る: u = k * np.random.uniform(0, 1.0, Nt)
- p_xがuより大きい候補点を採用する: tmp_sample = x[ np.where(p_x > u) ]
- 採用された候補点たちをary_sampleという配列に追加する: ary_sample = np.r_[ ary_sample, tmp_sample ]
- 現在までに採択されたサンプル数を求める: N_current = len(ary_sample)
- 採択されたサンプル数が所望のサンプル数を以上ならループ終了
ここで、f_q()はデフォルトではnp.random.uniform()なので、numpy配列を返します。
すなわちxはnumpy配列になります。
すると以降の計算もnumpy配列として計算が進みます。
処理5の棄却の処理もnumpyで行われます。
ループ終了後には、得られた採択サンプルの配列をN個に切り落とします。
これをreturnで返すことで棄却サンプルによる目標分布からのランダムサンプリングを終了します。
NumPy実装の利点 | 目標分布\(P\)の最大値が未知でも良い
第2回で紹介したNumPyを使わない実装方法では、提案分布が目標分布を覆うために、目標分布の最大値が既知である、あるいは解析的に計算できる必要がありました。
しかし、今回紹介した方法ではその必要はありません。
今回の実装方法では、予め全ての候補点の配列を作成します。
全ての候補点が求まっているために、これらの候補点の場所においてのみ、提案分布が目標分布を覆っていれば棄却サンプルを行うことができます。
したがって、全ての候補点における目標分布\(P\)の最大値を係数\(k\)とすれば良いわけです。
言い換えると、解析的にではなく、数値的に最大値を求めているわけです。
目標分布の設定
今回の例で、np_reject_sampling_1d()にf_pとして渡す目標分布は以下の箇所で定義されています。
# 目標の分布
def p(theta, d=100*1000., e=0.1):
return (d * (1-e**2) / (1-e))**1.5 / (1 + e*np.cos(theta))**2単に
$$
p(\theta) \propto \frac{\left(d_{P} \left(1 + e\right)\right)^{1.5}}{\left(1 + e \cos \theta \right)}
$$
を返す関数です。
関数p()には、変数(theta)の他に、dとeを渡すことができます。
これらは上の式の\(d_{P}\)と\(e\)に相当します。
棄却サンプリング関数の呼び出し
棄却サンプリングを行う関数np_reject_sampling_1d()を呼び出し、棄却サンプリングを実行する箇所は以下です。
np_reject_sampling_1d(p, N, f_q = np.random.uniform, arg_p = (d, e), arg_q = (-pi,pi), return_n_try = True)np_reject_sampling_1d()の第1引数は目標分布、第2引数はサンプルサイズなのでpとNを渡します。
arg_pという引数は、pの引数なので、タプル型でdとeを渡します。
arg_qは提案分布f_q、ここではnp.random.uniformなので、最小値と最大値を渡します。
return_n_tryをTrueにしておくと、whileループを回した回数が返ってきます。
たいていは1(ループが回らない)で返ってきます。
Conclusion | まとめ
最後までご覧いただきありがとうございます!
NumPyを使って棄却サンプリングを高速実装する例をご紹介しました!
pythonでは明示的なループ処理を書いてしまうと計算に時間がかかります。
NumPyライブラリを活用してループ処理を避けることで大幅に計算時間を短縮することができます!
ぜひトライしてみてください!
以上、「統計学&pythonレシピ | 任意の確率分布からのサンプリング4(NumPy棄却サンプリング編)」でした!
またお会いしましょう!Ciao!