みなさんこんにちは！このブログでは主に
の4つのトピックについて発信しています。
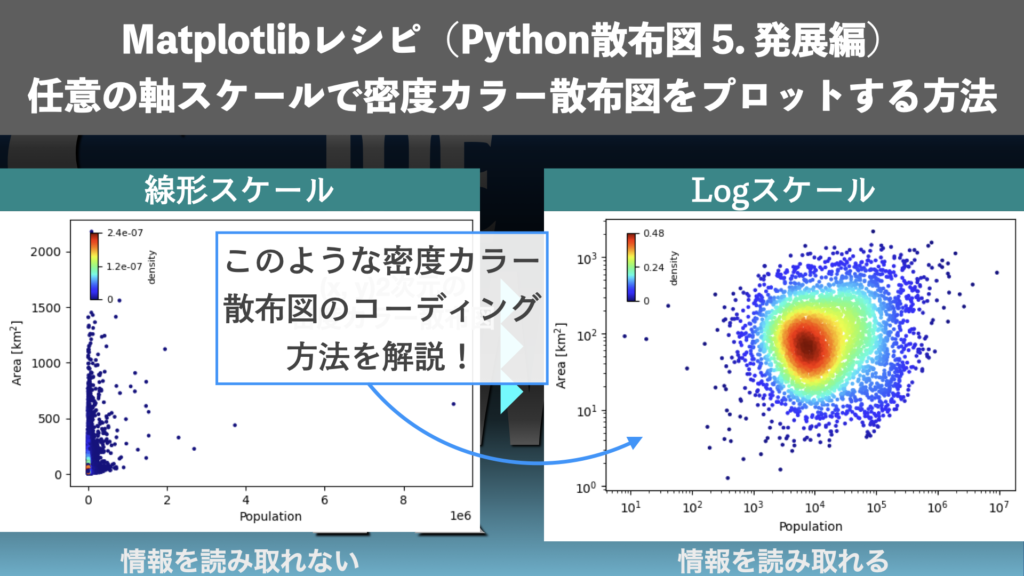
今回はpythonで綺麗な散布図を描く方法の第5回です！2次元の散布図上の点の密度をカラーで表示する「密度カラー散布図」の描画方法を具体的な実装例でご紹介します。今回は発展編として、任意の軸のスケールを設定した上で、密度カラー散布図をプロットする方法を紹介します！前回記事のMatplotlib、軸のスケールシリーズの内容も使います。
この記事を読めば、軸のスケールを設定した上で、pythonで綺麗な2次元散布図をプロットする方法を知ることができます！ぜひ最後までご覧ください。
Kaiko
この記事はこんな人のお悩み解決に役立ちます！
- Pythonの作図で綺麗な散布図を作りたいけど、どうしたら良い？
- y軸を対数スケールにして散布図を作りたい
- 負の値を含むデータだけど軸を対数スケールで散布図にしたい
- Abstract | 軸のスケールを変更することで様々なデータの密度カラー散布図を作れる！
- Background | 綺麗な散布図「密度カラー散布図」とその描画方法
- Method | 軸のスケールを設定して密度カラー散布図を描画する実装例
- Jupyter Notebookの用意
- ライブラリのインポート
- 関数の準備
- 密度カラー散布図を実際に描画する
- Linearスケールの密度カラー散布図
- 方法1（Linearスケール: 2次元ヒストグラム）
- 方法2（Linearスケール: 密度カラー散布図（ヒストグラム・スムージングなし・線形補間））
- 方法3（Linearスケール: 密度カラー散布図（ヒストグラム・スムージングなし・Digitize））
- 方法4（Linearスケール: 2次元ヒストグラム（スムージングあり））
- 方法5（Linearスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・線形補間））
- 方法6（Linearスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・Digitize））
- 方法7（Linearスケール: 密度カラー散布図（ヒストグラム・KDE））
- 方法8（Linearスケール: 密度カラー散布図（KDE））
- 方法1から方法8までのプロット結果（Linearスケール）
- Logスケールの密度カラー散布図
- NG例: Linearスケールでプロット
- 方法1（Logスケール: 2次元ヒストグラム）
- 方法2（Logスケール: 密度カラー散布図（ヒストグラム・スムージングなし・線形補間））
- 方法3（Logスケール: 密度カラー散布図（ヒストグラム・スムージングなし・Digitize））
- 方法4（Logスケール: 2次元ヒストグラム（スムージングあり））
- 方法5（Logスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・線形補間））
- 方法6（Logスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・Digitize））
- 方法7（Logスケール: 密度カラー散布図（ヒストグラム・KDE））
- 方法8（Logスケール: 密度カラー散布図（KDE））
- 方法1から方法8までのプロット結果（Logスケール）
- Log-Modulusスケールの密度カラー散布図
- NG例: Linearスケールでプロット
- 方法1（Log-Modulusスケール: 2次元ヒストグラム）
- 方法2（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・スムージングなし・線形補間））
- 方法3（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・スムージングなし・Digitize））
- 方法4（Log-Modulusスケール: 2次元ヒストグラム（スムージングあり））
- 方法5（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・線形補間））
- 方法6（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・Digitize））
- 方法7（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・KDE））
- 方法8（Log-Modulusスケール: 密度カラー散布図（KDE））
- 方法1から方法8までのプロット結果（Log-Modulusスケール）
- Linearスケールの密度カラー散布図
- Result | Pythonのサンプルコード
- Conclusion | まとめ
- References | 本シリーズの関連記事
Abstract | 軸のスケールを変更することで様々なデータの密度カラー散布図を作れる！
x軸やy軸のスケールを変更できるようにすることで、さまざまなデータを密度カラー散布図にプロットできます。密度カラー散布図にプロットするデータによっては、線形ではなく、対数(log)スケールなど、軸のスケールを適切なものに設定する必要があります。
変数が正規分布に近い場合は線形スケールのヒストグラムで表現できる一方で、変数が対数正規分布に近い場合には線形スケールでは潰れて見えないためlogスケールを取る必要があります。さらに、対数スケールのデータ（例: 人口の変化率）の変化などは負の値も表現できる対数が必要になります。
今回の記事では、x軸やy軸のスケールを変更して密度カラー散布図を作成する方法を、実際のコードの書き方の例で解説します。一連の処理を関数としてまとめるので、高度な処理も簡単に実装することができます。解説するソースコードをimportしたりコピー&ペーストしてすぐに使うこともできます！ぜひ本記事を最後までお読みください（長いですが）！
Background | 綺麗な散布図「密度カラー散布図」とその描画方法
まずは密度カラー散布図についておさらいしておきましょう。この記事は密度カラー散布図シリーズの第5回です。これまでに、
- Matplotlib | Pythonで綺麗な2次元散布図を描く方法（1. 概要編）
- Matplotlib | Pythonで綺麗な2次元散布図を描く方法（2. 理論編）
- Matplotlib | Pythonで綺麗な2次元散布図の実装方法とコードの書き方（3. 基礎編）
- Matplotlib | Pythonで散布図を1次元ヒストグラムと同時にプロットする方法（Python散布図 4. 応用編）
という記事で、密度カラー散布図の有用性と基本的な考え方や実装方法ご紹介してきました。これらの内容を簡単にまとめて、密度カラー散布図の有用性と描画方法の8つの分類を復習しましょう。
散布図は密度カラー散布図としてプロットすると見やすい
散布図を作成するとき、点と点が被って様子がわからなくなることがよくあります。点の密度をカラーで示す「密度カラー散布図」を使えば、点が密集していても分布の様子を表現することができます。
通常の散布図では点の密度が高い部分が潰れる
図1は正規分布に従うデータ点と双峰分布に従うデータ点を散布図にしたものです（詳細は過去記事「Matplotlib | Pythonで綺麗な2次元散布図を描く方法1（概要編）」参照）。図1の通常の散布図では中心部が潰れています。そのため、正規分布に従うデータと双峰分布に従うデータの区別ができません。
「密度カラー散布図」なら点の密度が高い部分も表現できる
一方、図2は密度カラー散布図です。点の密度をカラーで表現することで、データ点の密度が高い部分も表現できます。正規分布に従うデータ点と双峰分布に従うデータ点が明確に区別できます。データ点の密度が高い部分は情報量も多いため、このように的確に表現されるべきです。
密度カラー散布図の8通りの描画方法
密度カラー散布図の描画方法は
- 密度の計算方法
- スムージングの方法
- 個々の点への密度の割当方法
によって8つに分類することができます（図3）。方法5や6が様々な場面で使いやすい描画方法です。方法1と4は散布図ではなく2次元ヒストグラムの見た目になります。方法7や8はカーネル密度推定(KDE)を使うため、データ点の数が多いと計算時間が長くなります。
今回は図3の8つの密度カラー散布図の描画方法を実装するコード例を紹介します。
各描画方法の特徴や理論、基本的な実装方法の詳細は過去記事参照
図3の8つの描画方法の詳しい特徴や
- カーネル密度推定(KDE)
- 線形補間
- Digitize
などの用語や理論的な背景については過去記事
で解説しています。こちらもぜひご覧ください！
密度カラー散布図を単独で描画する基本的な実装方法についても過去記事
で解説していますので、こちらもご覧ください！
軸のスケール設定の必要性
密度カラー散布図にプロットするデータによっては、線形ではなく、対数(log)スケールなど、軸のスケールを適切なものに設定する必要があります。変数が正規分布に近い場合は線形スケールのヒストグラムで表現できる一方で、変数が対数正規分布に近い場合には線形スケールでは潰れて見えないためlogスケールを取る必要があります。さらに、対数スケールのデータの変化などは負の値も表現できる対数が必要になります。軸のスケール設定の必要性について、詳しくは過去記事
で解説していますので、そちらもご覧ください！
Method | 軸のスケールを設定して密度カラー散布図を描画する実装例
任意の軸のスケールを設定した上で密度カラー散布図を描画する例をご紹介します。
ここからはJupyter Notebookで一緒に作業することを想定し、一つ一つご紹介していきます。実際にはここで用いた関数を通常のPythonソースコードにコピーして使ったり、Pythonのファイルにまとめてimportして使うのが良いでしょう。ここでは簡単のためにJupyter Notebookで紹介します。
Resultの章にJupyter Notebookでの実装例を掲載するので、そちらを参照していただいても構いません。この章では、簡単な解説とともにソースコードを一つずつ提示します。解説が不要な方はResultの章に飛んでいただき、Jupyter Notebookでの実装例を参考にする方が早いでしょう。
Jupyter Notebookの用意
まずはJupyter Notebookのファイルを開きましょう。Jupyter Notebookの使い方については過去記事「python入門講座｜pythonを使ってみよう2(Jupyter Notebookを使う方法)[第5回]」もご覧ください！
ライブラリのインポート
まずはライブラリをインポートしておきます。NumPy, Scipy, Matplotlibなどを使います。以下を実行してください。
import time
import numpy as np
import scipy as sp
from scipy import stats
from scipy import interpolate
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import mpl_toolkits.axisartist as axisartist
import matplotlib.scale
関数の準備
密度の計算を行う関数や点への割振りを行う関数、作図する関数など、必要な関数を定義しておきます。
カラー密度散布図作成の基本的な関数
まずは以下の関数を準備しておきます。これらはカラー密度散布図作成で必ず必要となる基本関数です。
- KDEで(x, y)での密度を計算する関数:
get_density_with_KDE() - ヒストグラムで密度を計算する関数:
get_density_from_hist() - ヒストグラムを線形補間する関数:
get_interpolator_from_hist() - ヒストグラムから任意の点の密度を返す関数を作る関数:
get_func_from_histogram2d() - 一連の密度計算をまとめる関数（スケール非対応）:
get_scatter_density() - カラーバーを内側に作成する関数: `draw_inset_colorbar_on_ax()`
これら6つの関数は、過去記事「Matplotlib | Pythonで綺麗な2次元散布図の実装方法とコードの書き方（3. 基礎編）」で詳しく解説しています。今回の記事ではコードを紹介するに留めて詳しい解説を省きます。詳しい解説が必要な方は上記の過去記事を御覧ください！
KDEで(x, y)での密度を計算する関数
# get density at (x,y) using KDE with data points (x_i, y_i)
def get_density_with_KDE(
x:np.ndarray,
y:np.ndarray,
bw_method="scott",
wht_kde=None,
):
"""Get density at (x,y) using KDE with data points (x_i, y_i)
Args:
x (np.ndarray): x
y (np.ndarray): y
bw_method (str, optional): Bin width method passed to gaussian_kde. Defaults to "scott".
wht_kde (np.ndarray): weights
Returns:
v (np.ndarray): density at (x, y)
kernel (object): gaussian_kde kernel
"""
# KDE
kernel = sp.stats.gaussian_kde(
[x, y],
bw_method=bw_method,
weights=wht_kde
)
# get density
return kernel.pdf([x, y]), kernel
ヒストグラムで密度を計算する関数
# get density per bin using histogram
def get_density_from_hist(
x:np.ndarray,
y:np.ndarray,
bins=["auto","auto"],
density=True
):
"""Get density per bin using histogram
Args:
x (np.ndarray): x
y (np.ndarray): y
bins (list, optional): bins passed to histogram2d. Defaults to ["auto","auto"].
density (bool, optional): If True, density is pdf (\int{\rho dx dy} = 1), otherwise number per bin
Returns:
h_vals (np.ndarray): histogram values
x/y_bins (np.ndarray): histogram bins
x/y_cens (np.ndarray): center of bins
"""
# get bins for x and y
x_bins = np.histogram_bin_edges(x, bins=bins[0])
y_bins = np.histogram_bin_edges(y, bins=bins[1])
x_cens = 0.5*(x_bins[:-1] + x_bins[1:])
y_cens = 0.5*(y_bins[:-1] + y_bins[1:])
# histogram 2d
h_tmp, *_ = np.histogram2d(x, y, bins=[x_bins, y_bins], density=density)
h_vals = h_tmp.T
# end
return h_vals, x_bins, y_bins, x_cens, y_cens
ヒストグラムを線形補間する関数を作成する関数
# get interpolator from hist
def get_interpolator_from_hist(
x_cens:np.ndarray,
y_cens:np.ndarray,
v:np.ndarray,
fill_value=0.0,
bounds_error=False
):
"""Get interpolator
Args:
x_cens (np.ndarray): x bin center
y_cens (np.ndarray): y bin center
v (np.ndarray): histogram value
fill_value (float, optional): fill_value passed to scipy.interploate. Defaults to 0.0.
bounds_error (bool, optional): bounds_error passed to scipy.interpolate. Defaults to False.
Returns:
object: interpolation function (v = f_v([x, y]))
"""
# get interpolator
f_intrp = sp.interpolate.RegularGridInterpolator(
(x_cens, y_cens), v,
method="linear",
fill_value=fill_value,
bounds_error=bounds_error
)
# define a function
def f_dense_from_hist(xy):
"""
xy tuple of <1d array [N]>: x (xy[0]) and y (xy[1])
"""
# - get x and y - #
x, y = xy[0], xy[1]
# - get value - #
return f_intrp((x,y))
return f_dense_from_hist
ヒストグラムから任意の位置での密度関数を作成する関数
# get function to privide value at (x, y) from 2d histogram - #
def get_func_from_histogram2d(
x_edges:np.ndarray,
y_edges:np.ndarray,
h_vals:np.ndarray,
v_outer=[0.0, 0.0, 0.0, 0.0]
):
"""
description:
get function to provide pdf from histogram
arguments:
x_edges <1d array [n_bin_r+1]>: bin edges for r
y_edges <1d array [n_bin_rdot+1]>: bin edges for rdot
h_vals <2d array [n_bin_rdot, n_bin_r]>: histogram (pdf)
v_outer <list [4]>:
x<x_l and y<y_l: v_outer[0],
x<x_l and y>y_l: v_outer[1],
x>x_l and y<y_l: v_outer[2],
x>x_l and y>y_l: v_outer[3],
returns:
f_pdf <callable>: f_pdf(r,rdot) privides pdf
"""
# - define a function - #
def f_dense_from_hist(xy):
"""
xy tuple of <1d array [N]>: x (xy[0]) and y (xy[1])
"""
# - get x and y - #
x, y = xy[0], xy[1]
# - get index - #
i_x = np.digitize(x, x_edges)-1
i_y = np.digitize(y, y_edges)-1
idx_xy = np.where(
(0 <= i_x) & (i_x <= len(x_edges)-2) &
(0 <= i_y) & (i_y <= len(y_edges)-2)
)[0]
idx_e1 = np.where((0 <= i_x) & (i_y > len(y_edges)-2))[0]
idx_e2 = np.where((i_x > len(x_edges)-2) & (0 <= i_y))[0]
idx_e3 = np.where((i_x > len(x_edges)-2) & (i_y > len(y_edges)-2))[0]
# - get z - #
z = x * 0.0 + v_outer[0]
z[idx_xy] = h_vals[i_y[idx_xy], i_x[idx_xy]]
z[idx_e1] = v_outer[1]
z[idx_e2] = v_outer[2]
z[idx_e3] = v_outer[3]
# - return value - #
return z
# - end - #
return f_dense_from_hist
一連の密度計算をまとめる関数（スケール非対応）
# get scatter density
def get_scatter_density(
x:np.ndarray,
y:np.ndarray,
method_dense="hist",
method_smooth="conv",
method_points="interp",
bw_kde="scott",
bw_hist=["auto", "auto"],
dns_hist=True,
sig_smt=[2,2],
):
"""Get scatter density.
Args:
x (np.ndarray): x
y (np.ndarray): y
method_dense (str, optional): Method to calculate density. Defaults to "hist".
method_smooth (str, optional): Method for smoothing. Defaults to "conv".
method_points (str, optional): Method to get density at each point. Defaults to "interp".
bw_kde (str, optional): Bin width parameter for Gaussian KDE. Defaults to "scott".
bw_hist (list, optional): Bin width paramter for histogram. Defaults to ["auto", "auto"].
dns_hist (bool, optional): Density parameter for histogram. Defaults to True.
sig_smt (list, optional): Sigma [x, y] in smoothing. Defaults to [2,2].
Returns:
v (nd.array): density at (x,y)
f_v (object): function for density at arbitrary position
hist_vals (dict): "dense", "x_bins", "y_bins", "x_cens", "y_cens" from histogram
"""
# get density using histogram at first
h_vals, x_bins, y_bins, x_cens, y_cens = get_density_from_hist(
x, y, bw_hist, density=dns_hist
)
# calculate density
if method_dense == "kde":
# method 8: KDE
v, f_v = get_density_with_KDE(x, y, bw_kde) # v = f_v([x,y])
else:
# smoothing
if method_smooth == "kde":
# method7: hist2d + kde
x_ms, y_ms = np.meshgrid(x_cens, y_cens)
_, f_v = get_density_with_KDE(x_ms.ravel(), y_ms.ravel(), bw_kde, h_vals.ravel()) # v = f_v([x,y])
v = f_v([x, y])
else:
# apply smoothing
if (sig_smt[0] > 0 or sig_smt[1] > 0) and method_smooth == "conv":
h_vals = sp.ndimage.gaussian_filter(
h_vals, sig_smt, mode='nearest'
)
# map to points
if method_points == "interp":
# interpolate
f_v = get_interpolator_from_hist(x_cens, y_cens, h_vals.T)
v = f_v([x,y])
elif method_points == "digitize":
# digitize
f_v = get_func_from_histogram2d(x_bins, y_bins, h_vals)
v = f_v([x,y])
else:
# histogram
v, f_v = None, None
# histogram values into list
hist_vals = {
"dense": h_vals,
"x_bins": x_bins,
"y_bins": y_bins,
"x_cens": x_cens,
"y_cens": y_cens
}
# end
return v, f_v, hist_vals
カラーバーを内側に作成する関数
# draw inset color bar
def draw_inset_colorbar_on_ax(
ax:object,
ax_sct:object,
prm_clrbar={
'show':True,
'label':None,
'pos':[0.2,0.10,0.6,0.02],
'ori':'horizontal',
'fmt':'%.3g',
'n_ticks': 3,
'fs':10
}
):
"""Draw inset colorbar on ax
Args:
ax (object): Matplotlib axis object
ax_sct (object): Matplotlib PathCollection object returned from plt.scatter
prm_clrbar (dict, optional): Colorbar parameter. Defaults to { 'show':True, 'pos':[0.2,0.10,0.6,0.02], 'ori':'horizontal', 'fmt':'%.3g', 'n_ticks': 3, 'label':None, 'fs':10 }.
Returns:
cbar_ax (object): object returned from ax.inset_axes.
"""
# inset colorbar
if prm_clrbar['show']:
# get inset colorbar axis
cbar_ax = ax.inset_axes(prm_clrbar['pos'])
cbs = plt.colorbar(
ax_sct, cax=cbar_ax, orientation=prm_clrbar['ori'], format=prm_clrbar['fmt']
)
# ticks and ticklabels
try:
cbs.set_ticks(ax_sct.norm.inverse(np.linspace(0.0,1.0,prm_clrbar['n_ticks'])).data)
except:
print('** Warning, uninversible normalizer %s **' % (ax_sct.norm))
# label
cbs.set_label('%s' % (prm_clrbar['label']), size=prm_clrbar['fs'])
cbs.minorticks_off()
cbs.ax.tick_params(labelsize=prm_clrbar['fs'])
else:
cbar_ax = None
# end
return cbar_ax
スケール対応が必要な関数
のスケール設定に対応するため, 新たに以下の関数を定義する
- 一連の密度計算をまとめる関数（スケール対応）: `get_scatter_density_scaled()`
一連の密度計算をまとめる関数（スケール設定に対応）
スケール非対応で一連の密度計算をする関数「`get_scatter_density()`」の前後に変数変換を挟んだ関数を作成する。x軸とy軸のスケールを引数に取り、
- 変数変換
- 密度計算(`get_scatter_density()`)
- 変数逆変換
という処理を行う。
# get scatter density with x/y scale
def get_scatter_density_scaled(
x:np.ndarray,
y:np.ndarray,
method_dense="hist",
method_smooth="conv",
method_points="interp",
bw_kde="scott",
bw_hist=["auto", "auto"],
dns_hist=True,
sig_smt=[2,2],
x_scale="linear",
y_scale="linear"
):
"""Get scatter density.
Args:
x (np.ndarray): x
y (np.ndarray): y
method_dense (str, optional): Method to calculate density. Defaults to "hist".
method_smooth (str, optional): Method for smoothing. Defaults to "conv".
method_points (str, optional): Method to get density at each point. Defaults to "interp".
bw_kde (str, optional): Bin width parameter for Gaussian KDE. Defaults to "scott".
bw_hist (list, optional): Bin width paramter for histogram. Defaults to ["auto", "auto"].
dns_hist (bool, optional): Density parameter for histogram. Defaults to True.
sig_smt (list, optional): Sigma [x, y] in smoothing. Defaults to [2,2].
x_scale (str): scale for x. Select from mpl.scale.get_scale_names().
y_scale (str): scale for y. Select from mpl.scale.get_scale_names().
Returns:
v (nd.array): density at (x,y)
f_v (object): function for density at arbitrary position
hist_vals (dict): "dense", "x_bins", "y_bins", "x_cens", "y_cens" from histogram
v_trn (nd.array): density at transformed (x,y) for the scale
f_v_trn (object): function for density at arbitrary position at transformed (x,y) for the scale
hist_vals_trn (dict): "dense", "x_bins", "y_bins", "x_cens", "y_cens" from histogram (transformed (x,y) for the scale)
"""
# get scale & transfrm object
mpl_scl = {
"x": mpl.scale.scale_factory(x_scale, plt.subplot(111)),
"y": mpl.scale.scale_factory(y_scale, plt.subplot(111))
}
plt.close('all')
mpl_trn = {
"x": mpl_scl["x"].get_transform(),
"y": mpl_scl["y"].get_transform(),
}
mpl_inv = {
"x": mpl_trn["x"].inverted(),
"y": mpl_trn["y"].inverted()
}
# scale x, y
x_trn = mpl_trn["x"].transform(x)
y_trn = mpl_trn["y"].transform(y)
# get scatter density
v_trn, f_v_trn, hist_vals_trn = get_scatter_density(
x_trn, y_trn,
method_dense=method_dense, method_smooth=method_smooth, method_points=method_points,
bw_kde=bw_kde, bw_hist=bw_hist, dns_hist=dns_hist, sig_smt=sig_smt
)
# inverse trans form v
v = v_trn
# inverse transform f_v
def f_v(xy):
"""
xy tuple of <1d array [N]>: x (xy[0]) and y (xy[1])
"""
# transform xy
xy_trn = [
mpl_trn["x"].transform(xy[0]),
mpl_trn["y"].transform(xy[1])
]
# end
return f_v_trn(xy_trn)
# inverse transform hist_vals
hist_vals = {
"dense": hist_vals_trn["dense"],
"x_bins": mpl_inv["x"].transform(hist_vals_trn["x_bins"]),
"y_bins": mpl_inv["y"].transform(hist_vals_trn["y_bins"]),
"x_cens": mpl_inv["x"].transform(hist_vals_trn["x_cens"]),
"y_cens": mpl_inv["y"].transform(hist_vals_trn["y_cens"])
}
# end
return v, f_v, hist_vals, v_trn, f_v_trn, hist_vals_trn上記の関数について、簡単に解説します。まず、
x_trn = mpl_trn["x"].transform(x)
y_trn = mpl_trn["y"].transform(y)というところで、xとyを変数変換するところまでが前半部分です。ここまでのところでは、
mpl.scale.scale_factory()を使って、xxxScaleクラスを呼び出し、mpl_scl["x/y"]に格納mpl_scl["x/y"].get_transform()で、xxxTransformクラスを呼び出し、mpl_trn["x/y"]に格納mpl_trn["x/y"].inverted()で、InvertedxxxTransformクラスを呼び出し、mpl_inv["x/y"]に格納
という処理を行っています。スケール変換関数と逆変換関数を作成することが肝要です。Matplotlibのscaleについては、過去のシリーズ記事
- 第1回: Matplotlib | Python作図での軸のスケール設定の必要性（Python軸スケール 1. 知識編）
- 第2回: Matplotlib | 予め用意された7種類のスケール（Python軸スケール2）
- 第3回: Matplotlib | Scale Classの概要（Python軸スケール3）
- 第4回: Matplotlib | LogScale classとLog変換（Python軸スケール4）
- 第5回: Matplotlib | 自作のスケールを定義する方法: Custom scale（Python軸スケール5）
をご参照ください。
次に中盤部分の
v_trn, f_v_trn, hist_vals_trn = get_scatter_density(
x_trn, y_trn,
method_dense=method_dense, method_smooth=method_smooth, method_points=method_points,
bw_kde=bw_kde, bw_hist=bw_hist, dns_hist=dns_hist, sig_smt=sig_smt
)で、スケール変換された変数x_trn, y_trnから密度の計算を行います。
この後の後半部分では逆変換を行います。
v_trn: 計算された密度→v: 追加処理なしf_v_trn: 任意の場所の密度を返す関数→f_v(xy): xとy(変数変換前)から密度を返せるように修正hist_vals_trn: ヒストグラムのビン情報→hist_vals: xとyの値に戻るように逆変換
という処理を行ってv, f_v_trn, hist_vals_trnという変数を作ります。
任意スケールで密度カラー散布図をplotする関数
最後に、任意スケールで密度カラー散布図をplotする関数を作成します。任意スケールで密度の計算（get_scatter_density_scaled()）を行ったうえで、密度カラー散布図を描画する関数です。データ点のx座標, y座標を示す2つの1次元NumPy配列x, yを与えると、密度カラー散布図を描画することができます。
# get scatter-color plot
def plot_scatter_density_scaled(
x:np.ndarray,
y:np.ndarray,
method_dense:str="hist",
method_smooth:str="conv",
method_points:str="interp",
bw_kde="scott",
bw_hist=["auto", "auto"],
dns_hist=True,
sig_smt=[2,2],
x_scale="linear",
y_scale="linear",
figsize=[8,6],
label_xy=["x", "y"],
cmap=plt.cm.Greens,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
):
"""Plot scatter density
Args:
x (np.ndarray): x
y (np.ndarray): y
method_dense (str, optional): Method to calculate density. Defaults to "hist".
method_smooth (str, optional): Method for smoothing. Defaults to "conv".
method_points (str, optional): Method to get density at each point. Defaults to "interp".
bw_kde (str, optional): Bin width parameter for Gaussian KDE. Defaults to "scott".
bw_hist (list, optional): Bin width paramter for histogram. Defaults to ["auto", "auto"].
dns_hist (bool, optional): Density parameter for histogram. Defaults to True.
sig_smt (list, optional): Sigma [x, y] in smoothing. Defaults to [2,2].
x_scale (str): scale for x. Select from mpl.scale.get_scale_names().
y_scale (str): scale for y. Select from mpl.scale.get_scale_names().
figsize (list, optional): Figure size. Defaults to [8,6].
label_xy (list, optional): Label for x/y axis. Defaults to ["x", "y"].
cmap (object, optional): Color map. Defaults to plt.cm.Greens.
prm_clrbar (dict, optional): Colorbar parameter. Defaults to {'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}.
Returns:
v (nd.array): density at (x,y)
f_v (object): function for density at arbitrary position
hist_vals (dict): "dense", "x_bins", "y_bins", "x_cens", "y_cens" from histogram
"""
# time measurement
t_0 = time.time()
# get scatter density
(
v, f_v, hist_vals,
v_trn, f_v_trn, hist_vals_trn
) = get_scatter_density_scaled(
x, y,
method_dense=method_dense,
method_smooth=method_smooth,
method_points=method_points,
bw_kde=bw_kde,
bw_hist=bw_hist,
dns_hist=dns_hist,
sig_smt=sig_smt,
x_scale=x_scale,
y_scale=y_scale
)
# set figure
fig = plt.figure(figsize=figsize)
gs = gridspec.GridSpec(1,1)
axs = {}
# plot scatter density
i = 0
axs[i] = plt.subplot(gs[i])
axs[i].set_xlabel(label_xy[0])
axs[i].set_ylabel(label_xy[1])
axs[i].set_xscale(x_scale)
axs[i].set_yscale(y_scale)
if v is None:
ax_clr = axs[i].pcolormesh(
hist_vals["x_bins"], hist_vals["y_bins"], hist_vals["dense"],
cmap=cmap
)
else:
ax_clr = axs[i].scatter(
x, y, c=v,
cmap=cmap, s=10, lw=0.0, edgecolor='silver'
)
# inset colorbar
ax_cbar = draw_inset_colorbar_on_ax(axs[i], ax_clr, prm_clrbar=prm_clrbar)
# time measurement
t_1 = time.time()
print(' Elapsed Time: %.3g sec' % (t_1 - t_0))
# end
return v, f_v, hist_vals, v_trn, f_v_trn, hist_vals_trnこの関数では、最初にget_scatter_density_scaled()で密度カラー散布図に必要なデータを作成してから、そのデータをplotします。また、参考のために時間(t_1 – t_0)を測っています。
引数はget_scatter_density_scaled()とほとんど共通です。figsize以降の引数は図の大きさやカラーバーの種類を指定するパラメータです。
密度カラー散布図を実際に描画する
上記で定義した一連の関数を使って、実際に密度カラー散布図を実際に描画してみましょう。
- Linear(線形)スケール
- Log(対数)スケール
- Log-Modulusスケール
の3通りについて描画していきます。
Linearスケールの密度カラー散布図
まずはLinear(線形)スケールの密度カラー散布図を作成します。まずはデータを作成します。以下を実行してください。
# prepare data points 2
x2 = np.r_[
np.random.normal(loc=-1.0, scale=0.5, size=5000),
np.random.normal(loc=1.0, scale=0.5, size=5000)
]
y2 = x2 + np.random.normal(size=len(x2))データを作成したらプロットしていきます。方法1から方法8（図3参照）までの描画方法でプロットします。以下を順番に実行していきましょう。
方法1（Linearスケール: 2次元ヒストグラム）
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="none",
cmap=plt.cm.Greens
)方法2（Linearスケール: 密度カラー散布図（ヒストグラム・スムージングなし・線形補間））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="interp",
cmap=plt.cm.jet
)方法3（Linearスケール: 密度カラー散布図（ヒストグラム・スムージングなし・Digitize））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="digitize",
cmap=plt.cm.jet
)方法4（Linearスケール: 2次元ヒストグラム（スムージングあり））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="none",
cmap=plt.cm.Greens
)方法5（Linearスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・線形補間））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="interp",
cmap=plt.cm.jet
)方法6（Linearスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・Digitize））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="digitize",
cmap=plt.cm.jet
)方法7（Linearスケール: 密度カラー散布図（ヒストグラム・KDE））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="kde",
method_points="none",
cmap=plt.cm.jet
)方法8（Linearスケール: 密度カラー散布図（KDE））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="kde",
method_smooth="none",
method_points="none",
cmap=plt.cm.jet
)方法1から方法8までのプロット結果（Linearスケール）
上記を実行すると、図4のような密度カラー散布図が表示されます。
Logスケールの密度カラー散布図
次にLog(線形)スケールの密度カラー散布図を作成します。まずはデータを作成します。以下を実行してください。
# prepare data points 2
x2 = np.r_[
np.random.normal(loc=-1.0, scale=0.5, size=5000),
np.random.normal(loc=1.0, scale=0.5, size=5000)
]
y2 = 10**(x2 + np.random.normal(size=len(x2)))NG例: Linearスケールでプロット
データを作成したら、まずはLinearスケールプロットしてみましょう。以下を実行して方法5でプロットしてみましょう。
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="interp",
cmap=plt.cm.jet,
y_scale="linear"
)実行すると図5のようになり、分布の様子がわからない散布図になってしまいます。
方法1（Logスケール: 2次元ヒストグラム）
ここからは方法1から方法8（図3参照）までの描画方法でプロットします。以下を順番に実行していきましょう。
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="none",
cmap=plt.cm.Greens,
y_scale="log"
)方法2（Logスケール: 密度カラー散布図（ヒストグラム・スムージングなし・線形補間））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="interp",
cmap=plt.cm.jet,
y_scale="log"
)方法3（Logスケール: 密度カラー散布図（ヒストグラム・スムージングなし・Digitize））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="digitize",
cmap=plt.cm.jet,
y_scale="log"
)方法4（Logスケール: 2次元ヒストグラム（スムージングあり））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="none",
cmap=plt.cm.Greens,
y_scale="log"
)方法5（Logスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・線形補間））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="interp",
cmap=plt.cm.jet,
y_scale="log"
)方法6（Logスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・Digitize））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="digitize",
cmap=plt.cm.jet,
y_scale="log"
)方法7（Logスケール: 密度カラー散布図（ヒストグラム・KDE））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="hist",
method_smooth="kde",
method_points="none",
cmap=plt.cm.jet,
y_scale="log"
)方法8（Logスケール: 密度カラー散布図（KDE））
_ = plot_scatter_density_scaled(
x2,
y2,
method_dense="kde",
method_smooth="none",
method_points="none",
cmap=plt.cm.jet,
y_scale="log"
)方法1から方法8までのプロット結果（Logスケール）
上記を実行すると、図6のような密度カラー散布図が表示されます。図4と似たような図に見えますが、y軸をよく見るとLogスケールになっていることがわかるはずです。
図6ではy軸のスケールが見づらいので、方法5だけを図7に表示します。
Log-Modulusスケールの密度カラー散布図
次にLog-Modulusスケールの密度カラー散布図を作成します。Log-Modulusスケールを使うと、負の値を含むデータでも対数的に表示することができます。Log-Modulusスケールについては過去記事
をご参照ください。
まずはデータを作成します。以下を実行してください。
# prepare data points 3
x3 = np.r_[
np.random.normal(loc=-1.0, scale=0.5, size=5000),
np.random.normal(loc=1.0, scale=0.5, size=5000)
]
t = x3 + np.random.normal(size=len(x2))
y3 = np.sign(t) * (10**np.fabs(t)-1)NG例: Linearスケールでプロット
データを作成したら、まずはLinearスケールプロットしてみましょう。以下を実行して方法5でプロットしてみましょう。
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="conv",
method_points="interp",
cmap=plt.cm.jet,
y_scale="linear"
)実行すると図8のようになり、分布の様子がわからない図になってしまいます。
方法1（Log-Modulusスケール: 2次元ヒストグラム）
ここからは方法1から方法8（図3参照）までの描画方法でプロットします。以下を順番に実行していきましょう。
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="none",
method_points="none",
cmap=plt.cm.Greens,
y_scale="logmodulus"
)方法2（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・スムージングなし・線形補間））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="none",
method_points="interp",
cmap=plt.cm.jet,
y_scale="logmodulus"
)方法3（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・スムージングなし・Digitize））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="none",
method_points="digitize",
cmap=plt.cm.jet,
y_scale="logmodulus"
)方法4（Log-Modulusスケール: 2次元ヒストグラム（スムージングあり））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="conv",
method_points="none",
cmap=plt.cm.Greens,
y_scale="logmodulus"
)方法5（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・線形補間））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="conv",
method_points="interp",
cmap=plt.cm.jet,
y_scale="logmodulus"
)方法6（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・畳み込みスムージング・Digitize））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="conv",
method_points="digitize",
cmap=plt.cm.jet,
y_scale="logmodulus"
)方法7（Log-Modulusスケール: 密度カラー散布図（ヒストグラム・KDE））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="hist",
method_smooth="kde",
method_points="none",
cmap=plt.cm.jet,
y_scale="logmodulus"
)方法8（Log-Modulusスケール: 密度カラー散布図（KDE））
_ = plot_scatter_density_scaled(
x3,
y3,
method_dense="kde",
method_smooth="none",
method_points="none",
cmap=plt.cm.jet,
y_scale="logmodulus"
)方法1から方法8までのプロット結果（Log-Modulusスケール）
上記を実行すると、図9のような密度カラー散布図が表示されます。図4や図6と似たような図に見えますが、y軸をよく見るとLog-Modulusスケールになっていることがわかるはずです。
図9ではy軸のスケールが見づらいので、方法5だけを図10に表示します。
Result | Pythonのサンプルコード
今回のPythonコードの実装例を掲載します（Jupyter Notebook）。参考にどうぞ！
Conclusion | まとめ
最後までご覧頂きありがとうございます！
Pythonを使って、任意のx軸y軸スケールで密度カラー散布図を作成する方法をコードの実装例付きでご紹介しました！
x軸やy軸のスケールを変更できるようにすることで、さまざまなデータを密度カラー散布図にプロットできます。関数としてまとめておくことで、このような高度な処理も簡単に実装することができます。一度関数として定義したソースコードを持っておけば、importしたりコピー&ペーストしてすぐに使うことができます！ぜひ一度、やってみてください！
以上「Matplotlib | 任意の軸スケールで密度カラー散布図をプロットする方法（Python散布図 5. 発展編）」でした！
またお会いしましょう！Ciao！
References | 本シリーズの関連記事
本シリーズ「Pythonで綺麗な2次元散布図を描く方法」の関連記事は以下です。 第１回の概要編に加え、密度カラー散布図の描き方の分類（2. 理論編）、基本的な実装方法・コードの書き方（3. 基礎編）、1次元のヒストグラムと同時に描画する方法（4. 応用編）、軸のスケール設置を組み合わせる実装方法（5. 発展編）など、詳しく扱っておりますので参考にどうぞ！