みなさんこんにちは!このブログでは主に
の4つのトピックについて発信しています。
今回の記事では時系列データの分析について扱います!
本シリーズの前回記事↗では、ランダムウォークを例に 定数周りの定常性 をADF検定で確認しました。しかし実務で扱うデータ(株価・GDP・売上など)は、多くの場合 トレンドや時間項を含んだ非定常系列 です。
こうしたデータは「定数周りでは非定常」と判定されがちですが、実際には トレンドを取り除けば定常とみなせるケース も少なくありません。つまり、非定常の原因を正しく把握できれば、差分を取る以外にも、トレンド除去やモデル選択など 柔軟に適切な手法を選べる ようになります。
本記事では、トレンドや時間項を含むデータをPythonでシミュレーションし、ADF検定とKPSS検定 を用いて定常性を判定します。その過程で「非定常が何に起因するのか」を理解し、次のステップ(対処法やモデル選択)につながる前提知識を整理していきます。
Abstract | トレンドや時間項を含む非定常性を見極め、柔軟な分析手法を選ぶ
時系列データの分析において、非定常性をそのまま放置すると誤った結論につながります。
前回はランダムウォークを例に「定数周りの定常性」を確認しましたが、実務データ(株価・GDP・売上など)では多くの場合、トレンドや時間項が非定常の原因 となります。
本記事では、Pythonで生成したトレンド付き・時間項付きデータを用い、ADF検定とKPSS検定 によって定常性を判定します。その結果、「定数周りでは非定常と判定されても、トレンドを考慮すれば定常とみなせるケース」があることが確認できます。
この記事を読めば、非定常の原因を見極めることで、単なる差分処理に頼らず、トレンド除去やモデル選択など柔軟に正しい手法を選べるようになる ことが理解できます。
Introduction | 定常性の拡張
前回の記事では、ランダムウォークを例に「定数周りの定常性」を確認しました。つまり、平均や分散が時間に依存せず安定しているかどうかを基準に、データが定常か非定常かを判断したわけです。
しかし、実務で扱うデータはもう少し複雑です。株価やGDP、売上などのデータにはしばしば トレンド(長期的な増加や減少の傾向) や 時間項(二次曲線のような変化パターン) が含まれます。
この場合、定数周りでは非定常 と判定されがちですが、実際には「トレンドを取り除けば定常」とみなせることも多いのです。
このように、定常性には大きく分けて3つのレベルがあります。
- 定数周りの定常性:平均が一定(最も基本的なケース)
- トレンド周りの定常性:トレンドを取り除けば定常
- 時間項周りの定常性:時間項(二次曲線など)を取り除けば定常
つまり、データが非定常と判定されたとしても、その原因が何かを理解することが重要 です。
非定常の原因を正しく把握できれば、差分を取るだけでなく、トレンド除去や適切なモデル選択など、より柔軟に手法を選ぶことができるようになります。
そのために役立つのが、ADF検定 と KPSS検定 です。
- ADF検定:帰無仮説が「単位根あり(非定常)」
- KPSS検定:帰無仮説が「定常」
両者を組み合わせて活用することで、定常性の有無だけでなく、非定常の原因(トレンドか、時間項か、それともランダムウォークか) をより正確に見極められるようになります。
Method | トレンドや時間項を含むデータの生成と検定方法
本記事では、Pythonを用いて「定数周りでは非定常であるが、トレンドや時間項を考慮すれば定常」とみなせるケースをシミュレーションします。具体的には以下の 3通り \(\times\) 2種類 = 6種類 のデータを生成し、ADF検定とKPSS検定を適用します。
- 定数周りの定常・非定常データ
- ランダム変数(定常データの代表例)
- ランダムウォーク(非定常データの代表例)
- トレンド(ドリフト項)周りの定常・非定常データ
- トレンド付きランダム変数(トレンド周りに定常)
- ドリフト付きランダムウォーク(トレンド周りに非定常)
- 時間項周りの定常・非定常データ
- 時間項付きランダム変数(時間項周りに定常)
- 時間項付きランダムウォーク(時間項周りに非定常)
それぞれについて「定数周り」「トレンド周り」の検定を行い、結果を比較します。
定数周りの定常・非定常データ
定数周りの系列は、もっとも基本的な時系列データ です。平均や分散が一定で時間に依存しなければ「定常」、過去の値を累積するような構造を持つと「非定常」と判定されます。
ここではその代表例として、ランダム変数(ホワイトノイズ) と ランダムウォーク を生成します。
ランダム変数(定常データ)の生成
ランダム変数(ホワイトノイズ)は、平均と分散が一定で時間に依存しない典型的な 定常系列 です。
数式定義:
$$
x_{t} = \epsilon_{t}, \quad \epsilon_{t} \sim N(0, \sigma^2)
$$
Pythonコード:
import numpy as np
np.random.seed(42)
# sample size
n = 200
# random variable (white noise)
rand_var = np.random.normal(size=n)ランダムウォーク(非定常データ)の生成
ランダムウォークは、過去の値にノイズを足し合わせていく過程で、平均や分散が時間とともに変化するため 非定常系列 になります。
漸化式定義:
$$
x_{t} = x_{t-1} + \epsilon_{t}
$$
Pythonコード:
# random walk (cumulative sum of rand_var)
random_walk = np.cumsum(rand_var)時系列プロットで比較: 定数周りの定常・非定常データ
生成されたランダム変数とランダムウォークのデータを時系列のプロットで比較しておきましょう。
下の図1は、ランダム変数`rand_var`とランダムウォーク`random_walk`を時系列でプロットしたものです。
ランダム変数は平均と分散が一定の定常データですが、ランダムウォークは時間の経過によって平均や分散が変化する典型的な非定常データであることがわかります。
トレンド(ドリフト項)周りの定常・非定常データ
定数項に加えて線形トレンド(ドリフト) を持つ系列を考えます。この場合、単純な定数周りの検定では非定常と判定されやすいですが、トレンドを考慮すれば定常 と見なせる系列も存在します。ここでは代表的な2種類の系列を取り上げます。
トレンド付きランダム変数(トレンド周りに定常)の生成
線形トレンドにホワイトノイズを加えた系列です。トレンドを除去すれば残差は定常なので、トレンド周りに定常 となります。ランダムウォークと違い、トレンドが非確率的(=決定的)に現れるので、決定的トレンドと呼ばれることもあります。
数式定義:
$$
x_t = c_0 \cdot t + \epsilon_t
$$
Pythonコード:
# Trend + white noise (trend-stationary)
c0 = 0.05 # trend slope
trend_var = c0 * np.arange(n) + rand_varドリフト付きランダムウォーク(トレンド周りに非定常)の生成
ランダムウォークにドリフト項を加えた系列です。累積過程のため平均や分散が時間とともに発散し、トレンドを考慮しても非定常になります。
漸化式定義:
$$
x_{t} = x_{t-1} + c_{0} + \epsilon_{t}
$$
- \(c_{0}\):通常のランダムウォーク
- \(c_{0} \neq 0\):ドリフト付きランダムウォーク
Pythonコード:
# random walk with drift
c0 = 0.05 # drift term
drift_walk = np.cumsum(c0 + rand_var)時系列プロットで比較: トレンド周りの定常・非定常データ
トレンド周りの定常・非定常データについても時系列のプロットで比較しておきましょう。
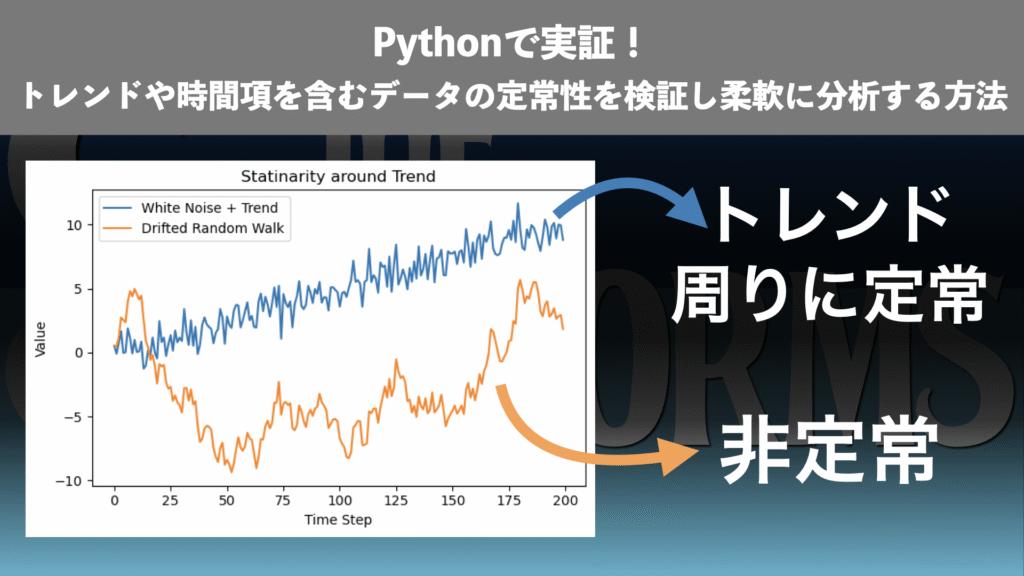
下の図2は、トレンド付きランダム変数`trend_var`とドリフト付きランダムウォークdrift_walkを時系列でプロットしたものです。
トレンド付きランダム変数は平均こそトレンドに従って変化しますが、分散は一定です。トレンドを除去すれば定常データとなります。一方、ドリフト付きランダムウォークの方は、トレンドよりもランダムウォークの効果によって平均や分散が変化しています。トレンドを除去しても非定常データであることが予想できます。
時間項周りの定常・非定常データ
ここでは、二次関数的な時間項(quadratic trend) を含む系列を考えます。
線形トレンドと同様、定数周りでは非定常と判定されることが多いですが、時間項を明示的にモデルに含めれば、時間項周りに定常 と見なせるケースがあります。
時間項付きランダム変数(時間項周りに定常)の生成
二次関数のトレンドにホワイトノイズを加えた系列です。時間項を回帰モデルで取り除けば残差は定常なので、時間項周りに定常 と呼ばれます。
数式定義:
$$
x_t = c_1 \cdot t^2 + \epsilon_t
$$
Pythonコード:
# Quadratic trend + white noise (time-stationary)
c1 = 0.001
time_var = c1 * (np.arange(n) ** 2) + rand_var時間項付きランダムウォーク(時間項周りに非定常)の生成
ランダムウォークに二次関数の時間項を加えた系列です。累積過程と非定常なトレンドが組み合わさるため、時間項を考慮しても非定常 になります。
漸化式定義:
$$
x_t = x_{t-1} + c_1 \cdot t + \epsilon_t
$$
Pythonコード:
# Quadratic trend + random walk (non-stationary)
c1 = 0.001
time_walk = np.cumsum(c1 * np.arange(n) + rand_var)時系列プロットで比較: 時間項周りの定常・非定常データ
時間項周りの定常・非定常データについても時系列のプロットで比較しておきましょう。
下の図3は、時間項付きランダム変数`time_var`と時間項付きランダムウォークtime_walkを時系列でプロットしたものです。
トレンド周りの定常・非定常データの例(図2↗)と同様の傾向ですが、図3ではトレンドが2次関数的に拡大する形となります。
ADF検定とKPSS検定の実行方法
ここまでで生成したデータに対して ADF検定 と KPSS検定 を適用します。それぞれの検定は以下のように補完的な役割を持っています。
- ADF検定(Augmented Dickey-Fuller Test)
- 帰無仮説:単位根あり(非定常)
- 対立仮説:単位根なし(定常)
- 小さいp値(< 0.05)の場合、定常と判定
regressionオプションで検定の種類を指定:"c"= 定数のみ"ct"= 定数+トレンド"ctt"= 定数+トレンド+時間項
👉 前回の記事↗で扱った検定です。主に「非定常かどうか」を確認するために使います。今回は「トレンド」や「時間項」を扱うため、ctやctt も実行対象に加えます。
- KPSS検定(Kwiatkowski-Phillips-Schmidt-Shin Test)
- 帰無仮説:定常
- 対立仮説:非定常
- 小さいp値(< 0.05)の場合、非定常と判定
regressionオプションで検定の種類を指定:"c"= 定数周りの定常性を検定"ct"= トレンド周りの定常性を検定
👉 ADF検定とは 逆の立場 を取ります。そのため、ADFとKPSSを併用することで判定の信頼性が高まる のがポイントです。
Pythonでの実装例は以下の通りです。検定結果は辞書に格納し、for文でループしてスッキリ表示するようにしました。
from statsmodels.tsa.stattools import adfuller, kpss
# function to run ADF and KPSS tests
def run_tests(series, name="series"):
# ADF test for options
adf_options = {
"c": "ADF (constant)",
"ct": "ADF (constant + trend)",
"ctt": "ADF (constant + trend + time)"
}
adf_results = {key: adfuller(series, regression=key)[1] for key in adf_options}
# KPSS test for options
kpss_options = {
"c": "KPSS (constant)",
"ct": "KPSS (trend)"
}
kpss_results = {key: kpss(series, regression=key)[1] for key in kpss_options}
# Print results
print(f"\n{name}")
for key, label in adf_options.items():
print(f"{label}: {adf_results[key]}")
for key, label in kpss_options.items():
print(f"{label}: {kpss_results[key]}")👉 これで、6種類のデータに対して定常性の検定を行う準備が整いました。
次章では Result として、実際の検定結果を比較していきます。
Result | Pythonで実証してみる
前章で準備した run_tests 関数を使って、6種類の系列に対して ADF検定 と KPSS検定 を実行していきます。それぞれのp値を確認することで、定常か非定常かを判定できます。
定数周りの定常・非定常データの検証
定数項周りの定常、非定常データの検証結果です。
ランダム変数(定常データ)
まずは基準となる ランダム変数(ホワイトノイズ) です。
# random variable (white noise)
run_tests(rand_var, name="Random Variable")- ADF(c, ct, ctt):すべて p < 0.05 → 定常
- KPSS(c, ct):すべて p > 0.05 → 定常
👉 両検定が一致し、典型的な 定常系列 と判定されます。
ランダムウォーク(非定常データ)
次に、典型的な非定常データである ランダムウォーク です。
# random walk
run_tests(random_walk, name="Random Walk")- ADF(c, ct, ctt):すべて p > 0.05 → 非定常
- KPSS(c, ct):すべて p < 0.05 → 非定常
👉 両検定が一致し、典型的な 非定常系列 と判定されます。
トレンド周りの定常・非定常データの検証
トレンド周りの定常、非定常データの検証結果です。
トレンド付きランダム変数(トレンド周りに定常)
まずは ランダム変数(ホワイトノイズ)+ トレンド です。
# Trend + white noise (trend-stationary)
run_tests(trend_var, name="Random Variable with Trend")- ADF(c):p > 0.05 → 非定常
- ADF(ct, ctt):p < 0.05 → 定常
- KPSS(c):p < 0.05 → 非定常
- KPSS(ct):p > 0.05 → 定常
👉 定数周りでは非定常ですが、トレンドを考慮すれば定常 と判定されます。
ドリフト付きランダムウォーク(トレンド周りに非定常)
続いて、ドリフト付きランダムウォーク を確認します。
# Random walk with drift
run_tests(drift_walk, name="Drifted Random Walk")- ADF(c, ct, ctt):p > 0.05 → 非定常
- KPSS(c, ct):p < 0.05 → 非定常
👉 ドリフトを加えてもランダムウォークは非定常のままであり、どの設定でも非定常と判定されます。
時間項周りの定常・非定常データの検証
時間項周りの定常、非定常データの検証結果です。
時間項付きランダム変数(時間項周りに定常)
まずは ランダム変数(ホワイトノイズ)+ 時間項 です。
# Quadratic trend + white noise (time-stationary)
run_tests(time_var, name="Random Variable with Quradratic Trend")- ADF(c, ct):p > 0.05 → 非定常
- ADF(ctt):p < 0.05 → 定常
- KPSS(c, ct):p < 0.05 → 非定常
👉 定数や線形トレンドでは非定常と判定されますが、時間項を考慮すれば定常 と判断されます。KPSS検定にはcttオプションが存在しないことにご注意ください。ADF検定のcttオプションのみで定常と判定されます。
時間項付きランダムウォーク(時間項周りに非定常)
最後に、時間項付きランダムウォークを確認します。
# Quadratic trend + random walk (non-stationary)
run_tests(time_walk, name="Random Walk with Quradratic Trend")- ADF(c, ct, ctt):p > 0.05 → 非定常
- KPSS(c, ct):p < 0.05 → 非定常
👉 強い非定常性が残り、時間項を考慮しても非定常のままです。
結果の比較(表で整理)
6種類の系列について、ADFとKPSSの結果を整理すると次のようになります。
| 系列 | ADF (c) | ADF (ct) | ADF (ctt) | KPSS (c) | KPSS (ct) | 判定のポイント |
|---|---|---|---|---|---|---|
| ランダム変数 | 定常 | 定常 | 定常 | 定常 | 定常 | 典型的な定常系列 |
| ランダムウォーク | 非定常 | 非定常 | 非定常 | 非定常 | 非定常 | 典型的な非定常系列 |
| トレンド付きランダム変数 | 非定常 | 定常 | 定常 | 非定常 | 定常 | トレンドを考慮すれば定常 |
| ドリフト付きランダムウォーク | 非定常 | 非定常 | 非定常 | 非定常 | 非定常 | 常に非定常 |
| 時間項付きランダム変数 | 非定常 | 非定常 | 定常 | 非定常 | 非定常 | 時間項を考慮すれば定常 |
| 時間項付きランダムウォーク | 非定常 | 非定常 | 非定常 | 非定常 | 非定常 | 時間項を考慮しても非定常 |
👉 この結果から、「どの基準で定常性を判定するか」によって結論が変わる ことが分かります。
単に「定常か非定常か」を判定するだけではなく、非定常性の要因(ランダムウォーク・トレンド・時間項)を見極めることが重要 です。
Discussion | 実務への示唆
時系列データの多くはそのままでは非定常であり、分析前に必ず確認が必要です。
今回の検証から導かれる実務への示唆は次の3点に整理できます。
- 実務データは多くが非定常であり、その原因を把握することが大切
- ADFとKPSSを併用すると判定の信頼性が高まる
- 非定常性の「性質」を理解することで、適切な分析手法を柔軟に選べる
以下、それぞれについて詳しく見ていきます。
実務データに潜む非定常の原因
今回のシミュレーションでは、ランダムウォーク・トレンド・時間項といった人工的な例を扱いましたが、実務で扱うデータも同様の特徴を持つことが多いです。
例えば:
- 株価や為替レート → ランダムウォーク的な動きを示す(非定常)
- GDPや売上高の長期推移 → トレンド(成長傾向)を含む
- 季節性を持つデータ → 時間項や周期構造によって非定常になる
👉 つまり、実務データの多くは「そのままでは非定常」であるため、必ず定常性を確認するステップ が必要です。
ADFとKPSSの併用で判定の信頼性を高める
今回の検定結果から分かるように、ADFとKPSSは仮説が逆 です。
- ADF:帰無仮説「非定常」
- KPSS:帰無仮説「定常」
したがって、両者を併用することで「定常/非定常」の判断をクロスチェックできます。
- 両者が一致すれば → 判定は強く信頼できる
- 食い違った場合 → 非定常性の原因(トレンドか、時間項か、ランダムウォークか)を深掘りする必要がある
👉 特に今回の「時間項付きランダム変数」のように、ADFとKPSSで異なる結論になるケースは 検定の仮定が異なるために起こる現象 です。
非定常の性質を知ることが分析戦略の幅を広げる
重要なのは「定常か非定常か」だけではなく、非定常性の原因が何なのか を見極めることです。
- ランダムウォーク型の非定常 → 差分を取る(I(1)系列)
- トレンドが原因の非定常 → トレンド除去やトレンドモデルを使う
- 時間項や周期性が原因の非定常 → 季節調整や周期モデルを使う
👉 このように、非定常性の性質を理解していれば、単純な差分に頼るのではなく、適切な前処理やモデル(ARIMA, VAR, トレンドモデルなど)を柔軟に選べる ようになります。
Conclusion | まとめ
本記事では、トレンドや時間項を含む場合の定常性 について検証しました。
- ランダム変数やランダムウォークに加えて、トレンド項や時間項を持つ系列を生成し、ADF検定とKPSS検定を適用しました
- 定数周りでは非定常と判定されても、トレンド周りや時間項を考慮すれば定常とみなせるケースがあることを確認しました
- 逆に、KPSS検定のように「トレンドまでしか仮定できない」検定では、時間項を含む系列は非定常と判定される限界があることも分かりました
👉 ポイントは、非定常の性質を知っておくことで、適切な前処理やモデル選択につなげられる という点です。単純に「定常/非定常」の二択ではなく、原因に応じた柔軟な分析戦略が重要になります。
次回予告
次回は、今回までに確認した「定常性の有無」を前提に、非定常データをどのように処理すればよいのか に焦点を当てます。
- 差分を取って定常化する
- トレンド除去を行う
- 季節調整を行う
- ARIMAなどのモデルを活用する
といった 具体的な対処法 を Python を使って実装し、実務データにも応用できる形で解説していきます。
👉 これで「偽相関の実証(第1回)↗」「定常性の確認(第2回)↗」「非定常の性質(第3回)」を踏まえ、いよいよ実践的な処理・モデリングの話へ進みます。
References | Pythonコードの全文
今回の記事で書いたPythonコード(Jupyter Notebook)の全文は以下です。ご参考にどうぞ!
時系列分析シリーズ
- 偽物の相関(76%)を実証!ランダムウォークに潜む落とし穴
- ADF検定で定常性を確認すべし
- (今回)トレンドや時間項を含む場合の定常性
- (次回)非定常データの対処法(差分・トレンド除去・季節調整・ARIMA)