Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
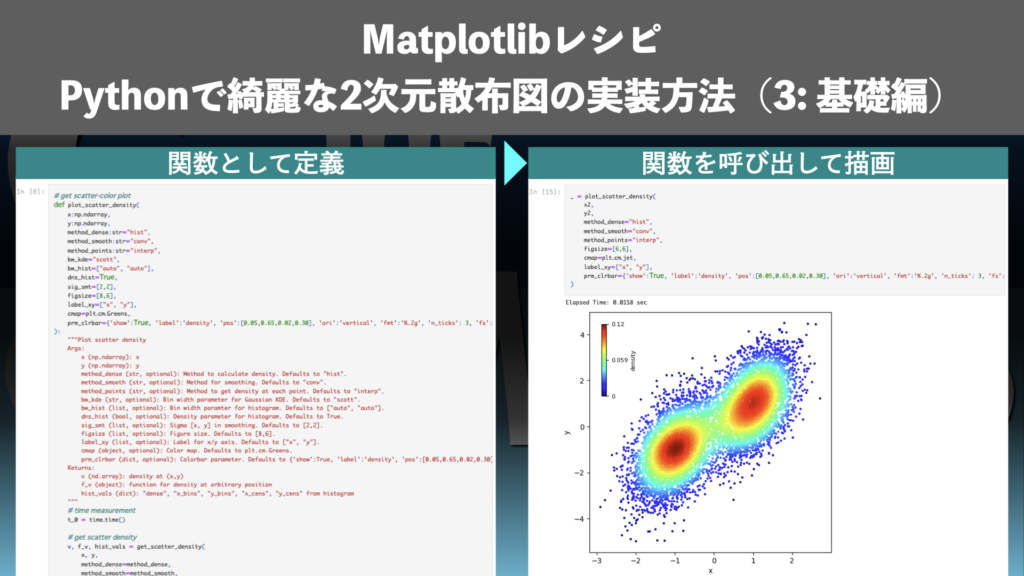
今回はpythonで綺麗な散布図を描く方法の第3回です!2次元の散布図上の点の密度をカラーで表示する「密度カラー散布図」の描画方法を具体的な実装例でご紹介します。まずは基礎編として、前回紹介した8つの描画方法を関数として実装します。
この記事を読めば、pythonで綺麗な2次元散布図をプロットする方法を知ることができます!ぜひ最後までご覧ください。
この記事はこんな人におすすめ
- Pythonでデータ解析をしている
- 散布図を綺麗に描きたい
Abstract | 関数として定義することで密度カラー散布図をすぐに描ける
密度カラー散布図を描画では、主要な機能を関数としてまとめて定義したソースコートを一度作っておくことがおすすめです。一度、まとまったソースコードを書いておけば、必要なときにimportしたりコピー&ペーストしてすぐに使うことができます。密度カラー散布図の描画には密度計算、スムージング、点への割振りといった工程が必要で、実装には少し手間がかかります。
密度計算を行う関数、点への割振りを行う関数、カラーバーを作る関数、描画する関数など、主要な機能ごとに関数としてまとめて実装しておくことで、密度カラー散布図を描きたい場面で簡単に描画することができます。今回の記事を見ながら、密度カラー散布図の実装をやってみてください!
Background | 密度カラー散布図と8つの描画方法
まずは密度カラー散布図についておさらいしておきましょう。この記事は密度カラー散布図シリーズの第3回です。これまでに、
という記事で、密度カラー散布図の有用性と基本的な考え方をご紹介してきました。これらの内容をおさらいしましょう。
散布図は密度カラー散布図としてプロットすると見やすい
散布図を作成するとき、点と点が被って様子がわからなくなることがよくあります。点の密度をカラーで示す「密度カラー散布図」を使えば、点が密集していても分布の様子を表現することができます。
通常の散布図では点の密度が高い部分が潰れる
図1は正規分布に従うデータ点と双峰分布に従うデータ点を散布図にしたものです(詳細は過去記事「Matplotlib | Pythonで綺麗な2次元散布図を描く方法1(概要編)」参照)。図1の通常の散布図では中心部が潰れています。そのため、正規分布に従うデータと双峰分布に従うデータの区別ができません。
「密度カラー散布図」なら点の密度が高い部分も表現できる
一方、図2は密度カラー散布図です。点の密度をカラーで表現することで、データ点の密度が高い部分も表現できます。正規分布に従うデータ点と双峰分布に従うデータ点が明確に区別できます。データ点の密度が高い部分は情報量も多いため、このように的確に表現されるべきです。
密度カラー散布図の8通りの描画方法
密度カラー散布図の描画方法は
- 密度の計算方法
- スムージングの方法
- 個々の点への密度の割当方法
によって8つに分類することができます(図3)。方法5や6が様々な場面で使いやすい描画方法です。方法1と4は散布図ではなく2次元ヒストグラムの見た目になります。方法7や8はカーネル密度推定(KDE)を使うため、データ点の数が多いと計算時間が長くなります。
今回は図3の8つの密度カラー散布図の描画方法を実装するコード例を紹介します。
各描画方法の特徴や理論の詳細は過去記事参照
図3の8つの描画方法の詳しい特徴や
- カーネル密度推定(KDE)
- 線形補間
- Digitize
などの用語や理論的な背景については過去記事
で解説しています。こちらもぜひご覧ください!
Method | 密度カラー散布図の基礎的な実装例
今回は密度カラー散布図の描画の8通りの方法の実装例をご紹介します。今回は基礎編として、x軸やy軸、密度を示すカラーの軸のスケールは線形のみとします。
ここからはJupyter Notebookで一緒に作業することを想定して、一つ一つ丁寧にご紹介していきます。実際にはここで用いた関数を通常のPythonソースコードにコピーして使ったり、Pythonのファイルにまとめてimportして使うといった形になると思います。ここでは簡単のためにJupyter Notebookで紹介します。
Resultの章にJupyter Notebookでの実装例を掲載するので、そちらを参照していただいても構いません。この章では、簡単な解説とともにソースコードを一つずつ提示します。解説が不要な方は、Resultの章に飛んでいただきJupyter Notebookでの実装例を参考にする方が早いのでオススメです!
ライブラリのインポート
まずはライブラリをインポートしておきます。NumPy, Scipy, Matplotlibを使います。
import time
import numpy as np
import scipy as sp
from scipy import stats
from scipy import interpolate
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import mpl_toolkits.axisartist as axisartist
関数の準備
密度の計算を行う関数や点への割振りを行う関数、作図する関数など、必要な関数を定義しておきます。以下の関数を準備しておきます。
- KDEで(x, y)での密度を計算する関数: 方法7と8の密度計算で利用
- ヒストグラムで密度を計算する関数: 方法1から7の密度計算で利用
- ヒストグラムを線形補間する関数を作成する関数: 方法2と5の点への割振りで利用
- ヒストグラムから任意の位置での密度関数を作成する関数: 方法3と6の点への割振りで利用
- 一連の計算をまとめる関数: 全ての方法の密度計算から点への割振りで利用
KDEで(x, y)での密度を計算する関数
方法7と方法8の密度計算で利用する関数を用意しておきます。カーネル密度推定(KDE)を使って点の密度を計算する関数です。データ点のx座標, y座標を示す2つの1次元NumPy配列x, yを与えると, 各(x, y)での密度とKDEのカーネルを返します。
# get density at (x,y) using KDE with data points (x_i, y_i)
def get_density_with_KDE(
x:np.ndarray,
y:np.ndarray,
bw_method="scott",
wht_kde=None,
):
"""Get density at (x,y) using KDE with data points (x_i, y_i)
Args:
x (np.ndarray): x
y (np.ndarray): y
bw_method (str, optional): Bin width method passed to gaussian_kde. Defaults to "scott".
wht_kde (np.ndarray): weights
Returns:
v (np.ndarray): density at (x, y)
kernel (object): gaussian_kde kernel
"""
# KDE
kernel = sp.stats.gaussian_kde(
[x, y],
bw_method=bw_method,
weights=wht_kde
)
# get density
return kernel.pdf([x, y]), kernelこの関数では、scipy.stats.gaussian_kdeを使って、KDEのカーネル関数を取得しています。そのカーネルを使って得られる(x, y)での密度kernel.pdf([x, y])とカーネル関数kernelを返します。
ヒストグラムで密度を計算する関数
方法1から7の密度計算で利用する関数を用意しておきます。2次元のヒストグラムで点の密度を計算する関数です。データ点のx座標, y座標を示す2つの1次元NumPy配列x, yを与えると, ヒストグラムの値とビンの両端と中心の座標を返します。
# get density per bin using histogram
def get_density_from_hist(
x:np.ndarray,
y:np.ndarray,
bins=["auto","auto"],
density=True
):
"""Get density per bin using histogram
Args:
x (np.ndarray): x
y (np.ndarray): y
bins (list, optional): bins passed to histogram2d. Defaults to ["auto","auto"].
density (bool, optional): If True, density is pdf (\int{\rho dx dy} = 1), otherwise number per bin
Returns:
h_vals (np.ndarray): histogram values
x/y_bins (np.ndarray): histogram bins
x/y_cens (np.ndarray): center of bins
"""
# get bins for x and y
x_bins = np.histogram_bin_edges(x, bins=bins[0])
y_bins = np.histogram_bin_edges(y, bins=bins[1])
x_cens = 0.5*(x_bins[:-1] + x_bins[1:])
y_cens = 0.5*(y_bins[:-1] + y_bins[1:])
# histogram 2d
h_tmp, *_ = np.histogram2d(x, y, bins=[x_bins, y_bins], density=density)
h_vals = h_tmp.T
# end
return h_vals, x_bins, y_bins, x_cens, y_censこの関数では、ビンの作成と2次元ヒストグラムの計算を行います。まず、numpy.histogram_bin_edgesを使ってx方向、y方向のビンをそれぞれ取得します。x_bins, y_binsはそれぞれx方向とy方向のビンの両端の座標となります。ビンの中心座標(x_cens, y_cens)も計算しておきます。
最後にnumpy.histogram2dで2次元のヒストグラムを得ます。densityの引数については、
- density=True: ヒストグラムの値は確率密度\(\rho(x_i, y_j)\)すなわち\(\sum_{i,j} \rho(x_i, y_j) \Delta x_i \Delta y_i = 1\)
- density=False: ヒストグラムの値はビン内のデータ点数(N/bin)
となります。上記の関数get_density_from_histのデフォルトではTrueとしてあります。KDEによる密度計算で得られる確率密度と整合する定義となります(ただしKDEは連続、ヒストグラムは不連続という差はあります)。
ヒストグラムを線形補間する関数を作成する関数
方法2と5の点への割振りで利用する関数を用意しておきます。2次元ヒストグラムの値とビンの中心座標から線形補間を行う関数を作成する関数です。ビンの中心座標とヒストグラムの値を与えると, 線形補間を行う関数を返します。
# get interpolator from hist
def get_interpolator_from_hist(
x_cens:np.ndarray,
y_cens:np.ndarray,
v:np.ndarray,
fill_value=0.0,
bounds_error=False
):
"""Get interpolator
Args:
x_cens (np.ndarray): x bin center
y_cens (np.ndarray): y bin center
v (np.ndarray): histogram value
fill_value (float, optional): fill_value passed to scipy.interploate. Defaults to 0.0.
bounds_error (bool, optional): bounds_error passed to scipy.interpolate. Defaults to False.
Returns:
object: interpolation function (v = f_v([x, y]))
"""
# get interpolator
f_intrp = sp.interpolate.RegularGridInterpolator(
(x_cens, y_cens), v,
method="linear",
fill_value=fill_value,
bounds_error=bounds_error
)
# define a function
def f_dense_from_hist(xy):
"""
xy tuple of <1d array [N]>: x (xy[0]) and y (xy[1])
"""
# - get x and y - #
x, y = xy[0], xy[1]
# - get value - #
return f_intrp((x,y))
return f_dense_from_histこの関数では、scipy.interpolate.RegularGridIntertpolatorを使って補間関数f_intrpを作成し、それをもとにf_dense_from_histを作って返しています。f_intrpを直接返してしまっても良いのですが、KDEで得られるカーネル関数と同じ形で引数を与えられるよう、f_dense_from_histに整形しています。
ヒストグラムから任意の位置での密度関数を作成する関数
方法3と6の点への割振りで利用する関数を用意しておきます。2次元ヒストグラムの値とビンの中心座標から任意の位置での密度を返す関数を作成する関数です。ビンの中心座標とヒストグラムの値を与えると, 任意の位置での密度を返す関数を返します。
# get function to privide value at (x, y) from 2d histogram - #
def get_func_from_histogram2d(
x_edges:np.ndarray,
y_edges:np.ndarray,
h_vals:np.ndarray,
v_outer=[0.0, 0.0, 0.0, 0.0]
):
"""
description:
get function to provide pdf from histogram
arguments:
x_edges <1d array [n_bin_r+1]>: bin edges for r
y_edges <1d array [n_bin_rdot+1]>: bin edges for rdot
h_vals <2d array [n_bin_rdot, n_bin_r]>: histogram (pdf)
v_outer <list [4]>:
x<x_l and y<y_l: v_outer[0],
x<x_l and y>y_l: v_outer[1],
x>x_l and y<y_l: v_outer[2],
x>x_l and y>y_l: v_outer[3],
returns:
f_pdf <callable>: f_pdf(r,rdot) privides pdf
"""
# - define a function - #
def f_dense_from_hist(xy):
"""
xy tuple of <1d array [N]>: x (xy[0]) and y (xy[1])
"""
# - get x and y - #
x, y = xy[0], xy[1]
# - get index - #
i_x = np.digitize(x, x_edges)-1
i_y = np.digitize(y, y_edges)-1
idx_xy = np.where(
(0 <= i_x) & (i_x <= len(x_edges)-2) &
(0 <= i_y) & (i_y <= len(y_edges)-2)
)[0]
idx_e1 = np.where((0 <= i_x) & (i_y > len(y_edges)-2))[0]
idx_e2 = np.where((i_x > len(x_edges)-2) & (0 <= i_y))[0]
idx_e3 = np.where((i_x > len(x_edges)-2) & (i_y > len(y_edges)-2))[0]
# - get z - #
z = x * 0.0 + v_outer[0]
z[idx_xy] = h_vals[i_y[idx_xy], i_x[idx_xy]]
z[idx_e1] = v_outer[1]
z[idx_e2] = v_outer[2]
z[idx_e3] = v_outer[3]
# - return value - #
return z
# - end - #
return f_dense_from_histこの関数では、numpy.digitizeを使って任意の座標をビンに割振り、そこでのヒストグラムの値を返す作業を行っています。ビンの外側の座標を指定されてもエラーにならないように工夫しているため少し複雑になっています。
一連の計算をまとめる関数
方法1から8のすべての方法に対応して密度計算、スムージング、点への割振りをまとめる関数を用意します。密度計算、スムージング、点への割振り方法を選択しながら、密度カラー散布図の描画に必要なデータを揃える関数です。データ点のx座標, y座標を示す2つの1次元NumPy配列x, yを与えると, 各(x, y)における密度vに加え、任意の場所の密度を与える関数f_v、2次元ヒストグラム関連の情報hist_valsを返します。
# get scatter density
def get_scatter_density(
x:np.ndarray,
y:np.ndarray,
method_dense="hist",
method_smooth="conv",
method_points="interp",
bw_kde="scott",
bw_hist=["auto", "auto"],
dns_hist=True,
sig_smt=[2,2],
):
"""Get scatter density.
Args:
x (np.ndarray): x
y (np.ndarray): y
method_dense (str, optional): Method to calculate density. Defaults to "hist".
method_smooth (str, optional): Method for smoothing. Defaults to "conv".
method_points (str, optional): Method to get density at each point. Defaults to "interp".
bw_kde (str, optional): Bin width parameter for Gaussian KDE. Defaults to "scott".
bw_hist (list, optional): Bin width paramter for histogram. Defaults to ["auto", "auto"].
dns_hist (bool, optional): Density parameter for histogram. Defaults to True.
sig_smt (list, optional): Sigma [x, y] in smoothing. Defaults to [2,2].
Returns:
v (nd.array): density at (x,y)
f_v (object): function for density at arbitrary position
hist_vals (dict): "dense", "x_bins", "y_bins", "x_cens", "y_cens" from histogram
"""
# get density using histogram at first
h_vals, x_bins, y_bins, x_cens, y_cens = get_density_from_hist(
x, y, bw_hist, density=dns_hist
)
# calculate density
if method_dense == "kde":
# method 8: KDE
v, f_v = get_density_with_KDE(x, y, bw_kde) # v = f_v([x,y])
else:
# smoothing
if method_smooth == "kde":
# method7: hist2d + kde
x_ms, y_ms = np.meshgrid(x_cens, y_cens)
_, f_v = get_density_with_KDE(x_ms.ravel(), y_ms.ravel(), bw_kde, h_vals.ravel()) # v = f_v([x,y])
v = f_v([x, y])
else:
# apply smoothing
if (sig_smt[0] > 0 or sig_smt[1] > 0) and method_smooth == "conv":
h_vals = sp.ndimage.gaussian_filter(
h_vals, sig_smt, mode='nearest'
)
# map to points
if method_points == "interp":
# interpolate
f_v = get_interpolator_from_hist(x_cens, y_cens, h_vals.T)
v = f_v([x,y])
elif method_points == "digitize":
# digitize
f_v = get_func_from_histogram2d(x_bins, y_bins, h_vals)
v = f_v([x,y])
else:
# histogram
v, f_v = None, None
# histogram values into list
hist_vals = {
"dense": h_vals,
"x_bins": x_bins,
"y_bins": y_bins,
"x_cens": x_cens,
"y_cens": y_cens
}
# end
return v, f_v, hist_valsこの関数では、
- 密度の計算方法を
method_dense - スムージング方法を
method_smooth - 点への割振り方法を
method_points
という引数で与えることで、方法1から方法8(図3)を選択することができます。method_denseは”hist”または”kde”とすることで、密度計算にヒストグラムを使うかKDEを使うかを選択できます。method_smoothは”conv”または”kde”とすることで、スムージングに畳み込みを使うかKDEを使うか選択できます。スムージングを行わない場合はmethod_smoothを上記以外の値(例えば”none”など)にします。method_pointsは”interp”または”digitize”とすることで、点への割振り方法を線形補間またはDigitizeとすることができます。点への割振りを行わない場合は上記以外の値とします。
カラーバーを図の内側に作成する関数
ここからはplotに必要な関数を定義していきます。まずはカラーバーを図の内側に作成する関数を作っておきます(inset color bar)。密度カラー散布図では、点の密度がカラーで示されるので、どの色がどの程度の密度に相当するかを示すカラーバーが必要です。図の内側に配置する方が見栄えが良いのでそのための関数を作っておきます。
# draw inset color bar
def draw_inset_colorbar_on_ax(
ax:object,
ax_sct:object,
prm_clrbar={
'show':True,
'label':None,
'pos':[0.2,0.10,0.6,0.02],
'ori':'horizontal',
'fmt':'%.3g',
'n_ticks': 3,
'fs':10
}
):
"""Draw inset colorbar on ax
Args:
ax (object): Matplotlib axis object
ax_sct (object): Matplotlib PathCollection object returned from plt.scatter
prm_clrbar (dict, optional): Colorbar parameter. Defaults to { 'show':True, 'pos':[0.2,0.10,0.6,0.02], 'ori':'horizontal', 'fmt':'%.3g', 'n_ticks': 3, 'label':None, 'fs':10 }.
Returns:
cbar_ax (object): object returned from ax.inset_axes.
"""
# inset colorbar
if prm_clrbar['show']:
# get inset colorbar axis
cbar_ax = ax.inset_axes(prm_clrbar['pos'])
cbs = plt.colorbar(
ax_sct, cax=cbar_ax, orientation=prm_clrbar['ori'], format=prm_clrbar['fmt']
)
# ticks and ticklabels
try:
cbs.set_ticks(ax_sct.norm.inverse(np.linspace(0.0,1.0,prm_clrbar['n_ticks'])).data)
except:
print('** Warning, uninversible normalizer %s **' % (ax_sct.norm))
# label
cbs.set_label('%s' % (prm_clrbar['label']), size=prm_clrbar['fs'])
cbs.minorticks_off()
cbs.ax.tick_params(labelsize=prm_clrbar['fs'])
else:
cbar_ax = None
# end
return cbar_ax必須の引数は
ax: カラーバーを配置するパネルのaxisオブジェクトax_sct: 散布図のaxisオブジェクト
です。どちらも次に登場する関数で定義されることになります。axはplt.subplot()などの返り値、ax_sctはplt.scatter()などの返り値として得られます。
任意の引数prm_clrbarはdict型として、いくつかのパラメータを持たせています。dictのkeyと値の意味は
- “show” (bool): カラーバーを表示するか?
- “labal” (str): カラーバーのラベル
- “pos” (list): カラーバーの位置と大きさ
- “ori” (str): カラーバーの方向
- “fmt” (str): カラーバーの数値のフォーマット
- “n_ticks” (int): カラーバーの目盛りの数
- “fs” (int): フォントサイズ
となります。prm_clrbar["pos"]の要素の意味は[カラーバー左下のx座標, カラーバー左下のy座標, x方向の幅, y方向の幅]となります。座標はグラフに表示されるx軸, y軸の目盛りとは無関係(絶対座標)で、0がグラフの左下の角、1がグラフの右上の角となります。
密度カラー散布図をplotする関数
密度カラー散布図をplotする関数を作成します。密度の計算を行ったうえで、密度カラー散布図を描画する関数です。データ点のx座標, y座標を示す2つの1次元NumPy配列x, yを与えると、密度カラー散布図を描画することができます。
# get scatter-color plot
def plot_scatter_density(
x:np.ndarray,
y:np.ndarray,
method_dense:str="hist",
method_smooth:str="conv",
method_points:str="interp",
bw_kde="scott",
bw_hist=["auto", "auto"],
dns_hist=True,
sig_smt=[2,2],
figsize=[8,6],
label_xy=["x", "y"],
cmap=plt.cm.Greens,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
):
"""Plot scatter density
Args:
x (np.ndarray): x
y (np.ndarray): y
method_dense (str, optional): Method to calculate density. Defaults to "hist".
method_smooth (str, optional): Method for smoothing. Defaults to "conv".
method_points (str, optional): Method to get density at each point. Defaults to "interp".
bw_kde (str, optional): Bin width parameter for Gaussian KDE. Defaults to "scott".
bw_hist (list, optional): Bin width paramter for histogram. Defaults to ["auto", "auto"].
dns_hist (bool, optional): Density parameter for histogram. Defaults to True.
sig_smt (list, optional): Sigma [x, y] in smoothing. Defaults to [2,2].
figsize (list, optional): Figure size. Defaults to [8,6].
label_xy (list, optional): Label for x/y axis. Defaults to ["x", "y"].
cmap (object, optional): Color map. Defaults to plt.cm.Greens.
prm_clrbar (dict, optional): Colorbar parameter. Defaults to {'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}.
Returns:
v (nd.array): density at (x,y)
f_v (object): function for density at arbitrary position
hist_vals (dict): "dense", "x_bins", "y_bins", "x_cens", "y_cens" from histogram
"""
# time measurement
t_0 = time.time()
# get scatter density
v, f_v, hist_vals = get_scatter_density(
x, y,
method_dense=method_dense,
method_smooth=method_smooth,
method_points=method_points,
bw_kde=bw_kde,
bw_hist=bw_hist,
dns_hist=dns_hist,
sig_smt=sig_smt
)
# set figure
fig = plt.figure(figsize=figsize)
gs = gridspec.GridSpec(1,1)
axs = {}
# plot scatter density
i = 0
axs[i] = plt.subplot(gs[i])
axs[i].set_xlabel(label_xy[0])
axs[i].set_ylabel(label_xy[1])
if v is None:
ax_clr = axs[i].pcolormesh(
hist_vals["x_bins"], hist_vals["y_bins"], hist_vals["dense"],
cmap=cmap
)
else:
ax_clr = axs[i].scatter(
x, y, c=v,
cmap=cmap, s=10, lw=0.0, edgecolor='silver'
)
# inset colorbar
ax_cbar = draw_inset_colorbar_on_ax(axs[i], ax_clr, prm_clrbar=prm_clrbar)
# time measurement
t_1 = time.time()
print(' Elapsed Time: %.3g sec' % (t_1 - t_0))
# end
return v, f_v, hist_vals
この関数では、最初にget_scatter_density()で密度カラー散布図に必要なデータを作成してから、そのデータをplotします。また、参考のために時間(t_1 – t_0)を測っています。
引数はget_scatter_density()とほとんど共通です。figsize以降の引数は図の大きさやカラーバーの種類を指定するパラメータです。
データ点の準備
これで必要な関数を定義することができたので、plotの例示に用いるデータ点を準備します。過去記事
でも登場した、普通の散布図では区別がつかない例を取り上げてみます。双方分布に従う点を1万個用意します。
# prepare data points 2
x2 = np.r_[
np.random.normal(loc=-1.0, scale=0.5, size=5000),
np.random.normal(loc=1.0, scale=0.5, size=5000)
]
y2 = x2 + np.random.normal(size=len(x2))
それぞれの方法でplotを作成
方法1から方法8(図3参照)までの方法で、密度カラー散布図を描いていきます。以下で示すように方法1から方法8をそれぞれ実行すると、図4にあるような密度カラー散布図を表示することができます。
方法1: 2次元ヒストグラム
方法1は「密度計算: ヒストグラム、スムージング: なし、点への割振り: なし」なので、ただの2次元ヒストグラムとなります。引数にmethod_dense="hist", method_smooth="none", method_points="none"を指定してplot_scatter_densityを実行します。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="none",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.Greens,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)なお、実行時間は私の環境では0.0194秒となりました。
方法2: 密度カラー散布図(ヒストグラム・スムージングなし・線形補間)
方法2では「密度計算: ヒストグラム、スムージング: なし、点への割振り: 線形補間」で密度カラー散布図を描きます。引数にmethod_dense="hist", method_smooth="none", method_points="interp"を指定してplot_scatter_densityを実行します。ちなみに密度カラー散布図の場合、cmapはjetが見やすいです。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="interp",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.jet,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.0206秒となりました。
方法3: 密度カラー散布図(ヒストグラム・スムージングなし・Digitize)
方法3では「密度計算: ヒストグラム、スムージング: なし、点への割振り: Digitize」として、密度カラー散布図を描きます。引数にmethod_dense="hist", method_smooth="none", method_points="digitize"を指定してplot_scatter_densityを実行します。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="none",
method_points="digitize",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.jet,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.0186秒となりました。
方法4: 2次元ヒストグラム(スムージングあり)
方法4では「密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: なし」として、スムージングされた2次元ヒストグラムを描きます。引数にmethod_dense="hist", method_smooth="conv", method_points="none"を指定してplot_scatter_densityを実行します。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="none",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.Greens,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.0171秒となりました。
方法5: 密度カラー散布図(ヒストグラム・畳み込みスムージング・線形補間)
方法5では「密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: 線形補間」として、密度カラー散布図を描きます。引数にmethod_dense="hist", method_smooth="conv", method_points="interp"を指定してplot_scatter_densityを実行します。短い計算時間で綺麗な密度カラー散布図を作ることができるおすすめの設定です。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="interp",
figsize=[6,6],
cmap=plt.cm.jet,
label_xy=["x", "y"],
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.0158秒となりました。
方法6: 密度カラー散布図(ヒストグラム・畳み込みスムージング・Digitize)
方法6では「密度計算: ヒストグラム、スムージング: 畳み込み、点への割振り: 線形補間」として、密度カラー散布図を描きます。引数にmethod_dense="hist", method_smooth="conv", method_points="digitize"を指定してplot_scatter_densityを実行します。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="conv",
method_points="digitize",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.jet,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.0108秒となりました。
方法7: 密度カラー散布図(ヒストグラム・KDE)
方法7では「密度計算: ヒストグラム、スムージング: KDE」として、密度カラー散布図を描きます。点への割振りはKDEで行われるので指定する必要はありません。引数にmethod_dense="hist", method_smooth="kde"を指定してplot_scatter_densityを実行します(method_pointsは任意の値で構いません)。
_ = plot_scatter_density(
x2,
y2,
method_dense="hist",
method_smooth="kde",
method_points="none",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.jet,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.0969秒となりました。方法1から6までよりも4から8倍程度長いです。
方法8: 密度カラー散布図(KDE)
方法8では「密度計算: KDE」として、密度カラー散布図を描きます。引数にmethod_dense="kde"を指定してplot_scatter_densityを実行します(method_smoothやmethod_pointsは任意の値で構いません)。すべてKDEで計算するので、計算時間が長くなる欠点があることに注意してください。
_ = plot_scatter_density(
x2,
y2,
method_dense="kde",
method_smooth="none",
method_points="none",
figsize=[6,6],
label_xy=["x", "y"],
cmap=plt.cm.jet,
prm_clrbar={'show':True, 'label':'density', 'pos':[0.05,0.65,0.02,0.30], 'ori':'vertical', 'fmt':'%.2g', 'n_ticks': 3, 'fs':8}
)実行時間は私の環境では0.459秒となりました。方法1から6までよりも20から40倍ほど時間がかかります。
Result | 実装例
今回のPythonコードの実装例を掲載します。こちらをご覧になったほうが、全体の流れはわかりやすいです。
Conclusion | まとめ
最後までご覧頂きありがとうございます!
Pythonで密度カラー散布図の実装方法をご紹介しました!
密度計算を行う関数、点への割振りを行う関数、カラーバーを作る関数、描画する関数など、主要な機能ごとに関数としてまとめて実装しておくと、密度カラー散布図を簡単に描くことができます。密度カラー散布図の描画には密度計算、スムージング、点への割振りといった工程が必要です。実装には少し手間がかかりますが、一度関数として定義したソースコードを持っておけば、importしたりコピー&ペーストしてすぐに使うことができます!ぜひ一度、実装してみてください!
以上「Matplotlib | Pythonで綺麗な2次元散布図の実装方法とコードの書き方(3. 基礎編)」でした!
またお会いしましょう!Ciao!
References | 本シリーズの関連記事
本シリーズ「Pythonで綺麗な2次元散布図を描く方法」の関連記事は以下です。 第1回の概要編に加え、密度カラー散布図の描き方の分類(2. 理論編)、基本的な実装方法(3. 基礎編)、1次元のヒストグラムと同時に描画する方法(4. 応用編)、軸のスケール設定を組み合わせる実装方法(5. 発展編)、任意の軸スケールで1次元ヒストグラムと同時に描画する方法(6.特別編)など詳しく扱っておりますので参考にどうぞ!
- Matplotlib | Pythonで綺麗な2次元散布図を描く方法(1. 概要編)
- Matplotlib | Pythonで綺麗な2次元散布図を描く方法(2. 理論編)
- Matplotlib | Pythonで綺麗な2次元散布図の実装方法(3. 基礎編)
- Matplotlib | Pythonで散布図を1次元ヒストグラムと同時にプロットする方法(4. 応用編)
- Matplotlib | 任意の軸スケールで密度カラー散布図をプロットする方法(Python散布図 5. 発展編)
- Matplotlib | 密度カラー散布図を任意の軸スケールで1次元ヒストグラムと同時にプロットする方法(Python散布図 6. 特別編)