みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
今回からmatplotlibの軸のスケールの設定方法について解説していきます!第1回の今回は図のスケールを設定する必要性についてお話します!作図する際、データによっては通常の線形スケールではデータ点が潰れて見にくくなってしまうため、Logスケールなどに設定する必要があります。今回は線形、Log、Symlogスケールを使うべき場面を例をあげて解説します!
この記事を読めば、作図する際に軸のスケールを変更べき場面を知ることができます!ぜひ最後までご覧ください。
この記事はこんな人におすすめ
- Pythonでデータ解析をしている
- 綺麗な図を作りたい
- Logスケールの必要性を知りたい
Abstract | 軸のスケールを適切に設定してわかりやすい図を作るべし
散布図やヒストグラム、その他さまざまな図を作る際、軸のスケールを適切に設定する必要があります。図で表現しようとしているデータの分布によっては、線形ではなく、対数(log)スケールなど、軸のスケールを適切なものに設定する必要があります。変数が正規分布に近い場合は線形スケールのヒストグラムで表現できる一方で、変数が対数正規分布に近い場合には線形スケールでは潰れて見えないためlogスケールを取る必要があります。他にも2つの変数をプロットするとき、一つの変数が1増えるともう一つが10倍になるなど変数が対数スケールで変化する場合にもlogスケールを使う必要があります。今回は具体例を交えて、線形スケールで済む場面、logスケールが必要な場面、さらに対称対数(Symmetrical-log; symlog)スケールが必要な場面をご紹介します。
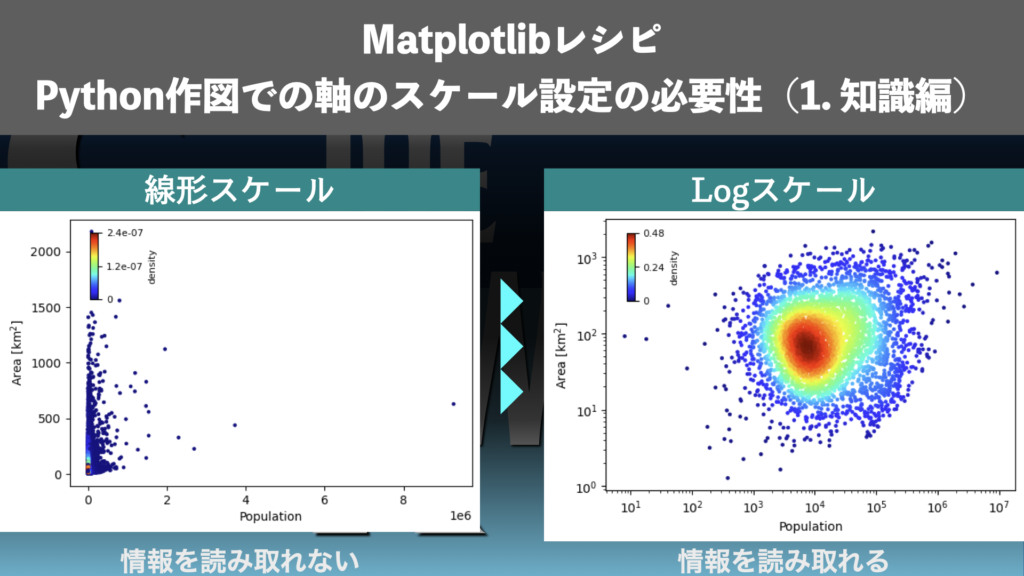
Backgrond | 軸のスケールが不適切だと情報を読み取れない
散布図やヒストグラムなどの図を作る際、軸のスケールを適切に設定できていないと情報を読み取ることができません。データの分布の様子や変数同士の相関関係を読み取るためには軸のスケールを適切に設定する必要があります。以下では軸のスケールが適切でない例と適切にした例を紹介します。
軸のスケールが不適切な例
図1は軸のスケールが適切に設定できておらず、情報が読み取ることができない例です。図1では、xとlog(y)が双方分布に従っており、xとyに相関関係があるデータを散布図にしています。ところが、y軸を線形スケールのままにしているため、データ点が双方分布に従っていることやxとyの相関関係を読み取ることができません。
軸のスケールを適切なものにした例
図2は図1のy軸をlogスケールに変更したものです。y軸をlogスケールに変更したことで、データの分布の様子がよくわかります。xとy(厳密にはlog(y))が双方分布になっており、相関関係があることを読み取ることができます。ちなみに図2では(実は図1でも)、散布図のカラーはデータ点の密度をあらわしており、赤いところほど密度が高いです。詳しくは過去記事「Matplotlib | Pythonで綺麗な2次元散布図を描く方法(1. 概要編)」をご参照ください。
今回扱う軸のスケール例
以下では実際に
- 線形スケール
- Logスケール
- symlogスケール
を設定する必要がある場面について、実データの具体例を取り上げて説明していきます。
線形スケール
線形スケールはデフォルトで使われるスケールで、軸の目盛りが1増えると変数も1増えるといったように、軸のスケールと変数のスケールが比例します。
Logスケール(対数スケール)
Logスケール(対数スケール)は、軸の目盛が1増えると変数は10倍になるといったように、軸のスケールに対して変数が倍々で増えていくスケールです。Logスケールでは0以下の数値を扱うことができないことに注意が必要です。
Symlogスケール(対称対数スケール)
Symlogスケール(対称対数スケール, Symmetrical Log Scale)は、0以下の数値もLogスケールで表示できるように工夫されたスケールです。0付近の一定の範囲、例えば-1から1までは線形、それより外側はLogスケールで表示できるようにしたものです。
それぞれのスケールの詳細や数理的な定義は次回以降の記事で扱うので、今回は具体例を通じてなんとなくの特徴だけ掴んでいただければ結構です。
Case 1 | 線形スケールで描画すべき場合
変数が正規分布するような場合や線形で変化する場合には、線形スケールでうまく描画することができます。例えば、変数が成人男性の身長や体重が該当します。成人男性の身長は、だいたい160 cmから180 cm程度と、170 cmの周りに正規分布するので線形スケールで綺麗に表現できます。体重もだいたい50 kgから70 kg程度の範囲で正規分布するため線形スケールで表現できます。また、身長が10 cm高い人は体重も10kg大きいといった線形な関係にあるため、身長と体重の散布図も線形スケールで表現できます。
線形スケールで描画すべきデータの例 | 成人の身長と体重
線形スケールで描画すべきデータの一例として、成人の身長と体重を取り上げます。成人の身長と体重のデータ例はKaggleで「Heights and Weights」というデータセットとして提供されています。このデータセットには25,000人の身長と体重が格納されており、csvとしてダウンロードすることができます。図3は「Heights and Weights」データセットの内容です。もともとのデータでは身長はインチ、体重はポンドという単位で記録されていますが、わかりにくいのでそれぞれcmとkgに変換したカラムを作っておきました。
成人の身長と体重のヒストグラム
「Heights and Weights」データセットを使ってヒストグラムを作ります。Pythonでの描画方法の解説は今回は省略し、作図の結果だけ示します。この記事の末尾にサンプルコードを掲載しているので、描画方法を知りたい方はそちらを御覧ください。
図4は身長と体重のヒストグラムです。図4からは身長が170から175 cmぐらいの周りに正規分布に近いかたちで分布していること、体重は60 kg弱の周りに正規分布に近い形で分布していることが読み取れます。ヒストグラムから分布の様子を読み取ることができるため、この例は線形スケールで描画することが適切である言えます。
成人の身長と体重の散布図
「Heights and Weights」データセットから身長と体重の散布図を作ります。点が密集するため、データ点の密度をカラーで示す密度カラー散布図でプロットします。密度カラー散布図については過去記事「Matplotlib | Pythonで綺麗な2次元散布図を描く方法(1. 概要編)」をご参照ください。描画方法の解説は省略しますが、この記事の末尾にサンプルコードを掲載しているので、描画方法を知りたい方はそちらを御覧ください。
図5は身長と体重の散布図です。図5からは身長と体重に相関があることが読み取れます。10 kg程度のばらつきはあるものの、身長が高いほど体重も大きいという関係を読み取ることができます。
このように、成人の身長や体重は線形スケールで表現することが適切です。ポイントとして、成人の身長は数cm程度の変化、体重も数kg程度の変化でしかないことが挙げられます。10倍や100倍といった差異ではなく、線形スケールで表現できる範囲に収まっています。
仮に成人の成人の身長や体重ではなく、あらゆる生物の体長と体重をプロットする場合には線形スケールではうまく表現できないと考えられます。なぜなら、体長数mmの昆虫と体長数mの大型哺乳類では体長に1000倍近い差異があり、線形スケールでは体長の小さい部分が潰れてしまって表現できないからです。このような変数が10倍、100倍といった差異を持つ、すなわち対数で分布する場合には対数スケールで描画すべきです。
Case 2 | Logスケールで描画すべき場合
変数が対数正規分布に近い場合や、桁で変化する場合にはlogスケールで描画する必要があります。例えば、
- 恒星の密度
- 鉱物の塊粒の寸法・重量
- 鉱床の規模
- 音の強さ
- 材料の寿命
- 生物群の個体数
- 生物個体の寸法・重量
- 市町村の人口
- 個人所得額
など、天文、地質、物理、生物、社会分野の様々な変数が対数正規分布に従っています。これらをわかりやすく表示するためにはlogスケールでプロットする必要があります。
Logスケールを使う必要がある変数の特徴
Logスケールを使う必要がある変数の特徴として
- 変数が正の数の場合で
- 変数の分布範囲が広い場合(小さな数と大きな数を同時に比べる場合)、あるいは
- 変数が10倍, 100倍, 1000倍, 10000倍と変化していく場合
が挙げられます。これらの特徴に当てはまる変数をプロットするときは軸をlogスケールにすることを考えてみてください。
Logスケールで描画すべきデータの例 | 市区町村の人口と面積
Logスケールで描画すべきデータの一例として、市区町村の人口と面積を取り上げます。市区町村の人口や面積は政府統計サイトe-Stat(外部サイトリンク)から取得できます。図6はe-Statからダウンロードした市区町村の統計データです。人口以外にも世帯数、面積、人口密度、人口増減や人口性比(女性100人に対する男性の数)といったカラムがあります。全国や都道府県単位のレコードも含まれていますが、今回は除外して使います。
市区町村の人口と面積を線形スケールで描画してしまった例
まずは市区町村の人口と面積を線形スケールで描画してみます。本来Logスケールで描画すべきデータを線形スケールで描画した場合に、情報がうまく読み取れないことを見ていきましょう。
市区町村の人口と面積のヒストグラムを線形スケールで描画
本来Logスケールでプロットすべきヒストグラムを線形スケールでプロットした場合、情報を読み取ることができません。図7は市区町村の人口と面積のヒストグラムを線形スケールで描画したものです。市区町村の人口や面積には桁で差異があるため、線形スケールでは数字の小さい部分が潰れてしまって情報を読み取ることができません。例えば、人口は10万人未満の市区町村が大半、面積は500km\(^2\)未満の市区町村が大半といったざっくりとした情報しか読み取ることができません。どの程度の人口や面積の市区町村が多いのか、人口や面積の分布幅がどの程度かといった重要な情報は、図7からは読み取ることができません。
市区町村の人口と面積の散布図を線形スケールで描画
散布図の場合もヒストグラム同様、本来Logスケールでプロットすべきデータを線形スケールでプロットすると情報を読み取ることができません。図8は市区町村の人口と面積を線形スケールで散布図にしたものです。図7のヒストグラムと同様、線形スケールでは数字の小さい部分が潰れてしまって情報を読み取ることができません。人口と面積にどの程度の相関があるのか、分散はどの程度かといった重要な情報を読み取ることはできません。
市区町村の人口と面積をLogスケールで描画する例(本来あるべき姿)
次に市区町村の人口と面積をLogスケールで描画してみます。Logスケールで描画すべきデータは、logスケールで描画すると情報をうまく読み取れるということを確認していきましょう。
市区町村の人口と面積のヒストグラムをLogスケールで描画
本来LogスケールでプロットすべきヒストグラムをLogスケールでプロットした場合、重要な情報を読み取ることができます。Logスケールのヒストグラムを作る場合、ビンもLogスケールで均等になるように作成することがポイントです。実装方法の詳細については末尾のサンプルコードをご覧ください。
図9は市区町村の人口と面積のヒストグラムをLogスケールで描画したものです。x軸をLogスケールにしたことで、正規分布に近い形の分布で表示され、平均や分散といった重要な情報が読み取れるようになったことがわかります。例えば、市区町村の平均的な人口は1万人程度、面積は100km\(^2\)程度であることがわかります。分布の幅も、人口は1000人から10万人、面積は10km\(^2\)から1000km\(^2\)程度であることが読み取れます。
市区町村の人口と面積の散布図をLogスケールで描画
散布図も本来LogスケールでプロットすべきデータはLogスケールでプロットすると、情報を読み取ることができます。図10は市区町村の人口と面積をLogスケールで散布図にしたものです。人口と面積の分布の様子がよくわかります。人口と面積には弱い相関がある程度で、分散が大きいといった情報を読み取ることができます。市区町村単位で比較しても広くて人口が多い地域もあれば人口が少ない地域もあるし、狭い地域でも人口が多い地域もあるといった情報を得ることができます。こういった情報は、図8のように線形でプロットしてしまうと読み取ることができません。
Case 3 | Symlogスケールで描画すべき場合
変数が10倍、100倍と桁で変化する上に、負の数も取るような場合にはSymlogスケール(Symmetrical Log Scale, 対称対数スケール)が有効です。例えば、市区町村の人口増減数は100人増える地域もあれば1万人増える地域もあるし、100人減る地域も1万人減る地域も存在します。100人、1000人、1万人を同時に比較するためにはLogスケールにする必要がありますが、値が0以下になるため普通のLogスケールでは対応できません。このような場合にSymlogスケールを使います。
Symlogスケールで描画すべきデータの例 | 市区町村の人口増減数
Symlogスケールで描画すべきデータの一例として、市区町村の人口増減数を取り上げます。データセットはLogスケールの例と同様、政府の統計サイトe-Stat(外部リンク)から取得したものです。図6に示した表の「5年間の人口増減数【人】」というカラムを用います。
市区町村の人口増減のヒストグラム
市区町村の5年間の人口増減のヒストグラムを図11に示します。x軸をSymlogスケールにすることで情報を読み取ることができます。人口減少の市区町村と人口増加の市区町村の二山の分布となっていることがわかります。さらに人口減少の市区町村が圧倒的に多いことが読み取れます。また、人口減少や人口増加の範囲は1000人を中心に100から1万人程度であることもわかります。分布の様子がよくわかり重要な情報も読み取ることができるため、Symlogスケールによるプロットが適切であることがわかります。
市区町村の人口と人口増減の散布図
市区町村の人口と人口増減の散布図を作ってみます。図12は市区町村の人口と5年間の人口増減の散布図です。x軸(人口)はlogスケール、y軸(人口増減)はSymlogスケールとなっています。このようにスケールを設定したことで重要な情報を読み取ることができます。例えば、図12からは人口減少傾向の市区町村と人口増加傾向の市区町村とに分かれており、大半の市区町村で人口が減少していることがわかります。人口1万人弱ぐらいで5年間で人口が1000人弱減少する市区町村が多い(散布図の赤い色の部分)ようです。少数派の人口増加傾向の市区町村のほとんどが人口1万人以上であることも読み取れます。ついでに図12には人口増減率約\(\pm\)1%、\(\pm\)10%、\(\pm\)100%を示す点線、丸点線、破線を記入しました。人口減少傾向の市区町村では人口減少率が10%以上の市区町村も少なからず存在しますが、人口増加率が10%を超える市区町村はほとんど存在しないこともわかります。このように軸のスケールを適切に設定することで様々な情報を読み取ることができます。
Code | Pythonのサンプルコード
今回のPythonコードの実装例を掲載します(Jupyter Notebook)。参考にどうぞ!
Conclusion | まとめ
最後までご覧頂きありがとうございます!
図をプロットする際の軸のスケール設定の必要性についてお話しました!
表示したいデータの性質に合わせて軸のスケールを設定することで、重要な情報を読み取ることができる図を作ることができます。軸のスケールには線形、Log(対数)、Symlog(対称対数)、その他様々あります。自然界や社会のデータには線形スケールではうまく表現できないデータも多く存在します。今回ご紹介した例を参考に、データの分布を調べて適切なスケールでプロットしてみてください!
以上「Matplotlib | Python作図での軸のスケール設定の必要性(1. 知識編)」でした!
またお会いしましょう!Ciao!
References | 参考
参考をまとめます。
参考外部サイト
今回プロットした例のデータや対数正規分布の例については以下のサイトをご覧ください。
- 身長・体重データ: Kaggle Heights and Weights Data Set(外部サイト)
- 対数正規分布: 独立行政法人エネルギー・金属鉱物資源機構(外部サイト)
- 市区町村の人口: 政府統計サイトe-Stat(外部サイト)
関連記事
密度カラー散布図については以下の過去記事をご覧ください。