Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信しています。
2025年冒頭では、新シリーズ「天文学者のマクロ経済学」をしばらくの間お届けします!2024年末ごろから、基礎控除引き上げによる減税や財政収支(プライマリーバランス)の黒字化が話題ですね。マクロ経済の概念は、天文学の一分野である銀河の形成進化の研究で使われるモデルによく似た部分があると感じました。そこで、天文学者としてマクロ経済について考察してみることにしてみました!
このシリーズ「天文学者のマクロ経済学」では、
- マクロ経済モデルの概観 | 3人の登場人物とお金の流れ
- 企業の役割 | モノの生産 ←今回
- 政府の役割 | 通貨流通量の調整
- 政府収支と物価 | 財政収支黒字化は目標として不適切
- 技術革新と物価 | 技術革新もデフレ化を招き得る
- 貿易と物価 | 日本は貿易黒字によるインフレを狙っている?
- 日本の財政政策 | デフレに逆戻りしないためにどうすべき?
といった内容を解説する予定です!
#2の今回は、マクロ経済モデルにおける企業の役割を解説します。この記事を読めば、経済成長する限り国の中でモノが増え続けることを知ることができます!次回解説する政府の役割の前提となる内容です。ぜひ最後までご覧ください!
この記事はこんな人におすすめ
- 基礎控除引き上げの議論で経済に興味を持った
- 政府の財政黒字化が正しいのか間違っているのかわからない
- “国の借金”のことがなんとなく心配
Abstract | 企業の役割はモノの生産。そしてモノは増え続ける
マクロ経済モデルでは、政府、企業、家計の3人だけの登場人物を設定し、国の中でのお金の流れをこの3人の間でのやりとりとして考えます。企業の役割はモノの生産、すなわち政府や家計から供給される資金、また家計から供給される労働力をもとに、商品やサービスといったモノを生産し、市場に供給することです。市場により質の高いモノが増えていくことで、国民の生活が豊かになっていきます。
さらに今回はモノの供給に着目し、企業が成長する限り、すなわち経済が成長し、技術革新や生産性の工場が続く限り、市場に残されるモノの価値の総量は増え続けるというお話をします。ある年に市場に新たに供給されるモノの価値の総量がどのように変化し、将来的にすべてのモノの価値の総量がどのように推移するかを考察します。
Background | マクロ経済モデルの前提のおさらい
まずはマクロ経済モデルについておさらいしましょう。前回の第1回では、
という内容を扱いました。登場人物は政府、企業、家計の3人だけであること、お金の流れはこの3人の間でやりとりする6種類だけであることをお話しました。さらに、貿易収支均衡の仮定を置くことによって、国を一つの閉じた系と考えることができることもお話しました。
今回は一つの閉じた系である国において、登場人物の一人である企業の役割を解説していきます。
Data | マクロ経済モデルにおける企業の役割 | モノの生産
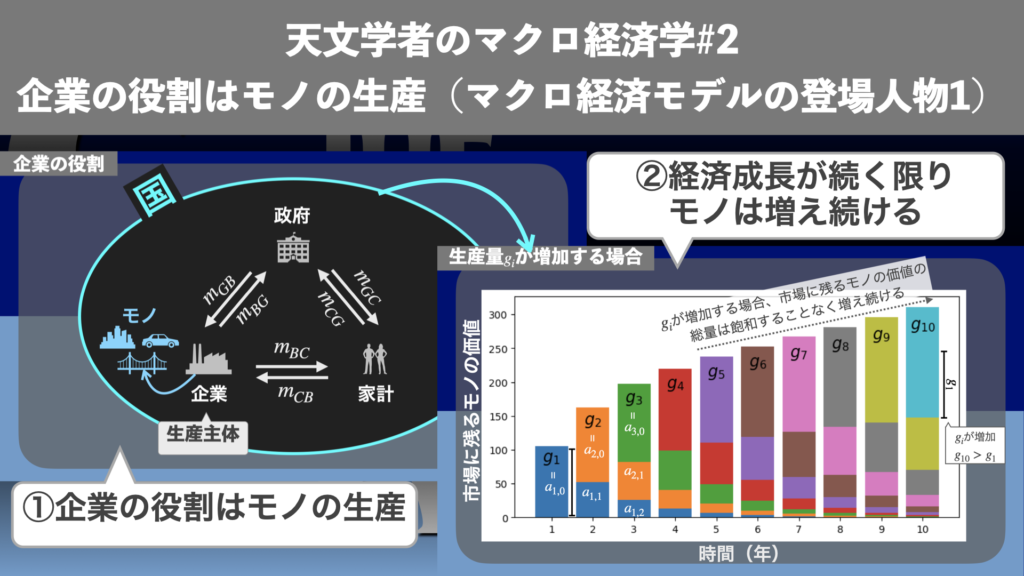
マクロ経済モデルにおける企業の重要な役割はモノの生産です。政府からの出資や家計(個人)からの出資や売上を元手にモノを生産し、市場に供給します(図1)。図1の記号の詳細は前回記事「天文学者のマクロ経済学#1 導入編|マクロ経済モデルの概観(3人の登場人物とお金の流れ)」を参照してください。図1で示したとおり、企業は入ってくるお金(\(m_{GB}やm_{BC}\))と家計から供給される労働力をもとに、商品やサービスといったモノを生産し市場に供給します。市場により良いものモノが増えていくことで、生活が豊かになっていきます。なお、ここで言うモノとは、橋や道路、車などの固定資産になる商品だけでなく、食べ物や文房具といった消費財、サービスなどあらゆる商品やサービスをモノとして総称する抽象的な概念であることに注意してください。
企業が成長する限りモノは増え続ける
ここで、企業が成長する限りは市場にモノが増えていくことに注意が必要です。企業の成長や生産性の向上によって1年間に創出できるモノの価値の総量は増える一方、1年間に失われるモノの価値の総量は減っていくため、市場に残されるモノの価値はどんどん増えていきます。以下で詳しく見ていきましょう。
Method | 生産されたモノの価値の時間変化を定式化
市場に残されるモノの価値の総量について考えるために、まずは企業活動によって生産されたモノの価値の総量が、時間とともにどのように変化していくかをモデル化していきます。ある年に生産されたモノは消費や経年劣化によって価値が減少していきます。この様子を単純化して定式化します。
ある年に生産されたモノの価値の総量の時間変化の定式化
ある年\(i\)に生産されたモノの価値の総量が時間とともにどのように変化していくかを考え、定式化していきます。まず、ある年\(i\)に新たに生産されたモノの価値の総量を\(g_{i}\)と書くことにします。モノは消費や経年劣化によって価値が減少していきます。すぐに消費される商品やサービスであれば消費、耐用年数の長いインフラや設備であれば経年劣化が想定されます。\(i\)年に生産されたモノについて、\(j\)年後の価値の減少量を\(r_{i,j}\)と書くことにします。
次に、\(i\)年に生産されたモノについて、\(j\)年後に残存する価値の総量を考えます。\(i\)年に生産されたモノの\(j\)年後の残存価値の総量を\(a_{i,j}\)と書くことにします。前年の\(j-1\)年後との関係を考えると、\(j-1\)年後の価値の総量\(a_{i,j-1}\)から\(r_{i,j}\)だけ減少するので、
$$
a_{i, j} = a_{i, j-1} – r_{i,j} \tag{1}
$$
という漸化式を作ることができます。この漸化式を進めていくと、\(i\)年に生産されたモノのうち\(j\)年後に残存する価値の総量は
$$
a_{i, j} = a_{i, 0} – \sum_{k=1}^{j} r_{i,k} \tag{2}
$$
となります。さらに0年後に残存する価値の総量\(a_{i, 0}\)は、\(i\)年に生産されたモノの価値の総量と同じなので、\(a_{i, 0} = g_{i}\)です。
式(1)と(2)から、\(g_{i}\)と\(r_{i,j}\)を用いて、\(i\)年に生産されたモノについて、\(j\)年後に残存する価値の総量は
$$
a_{i, j} = g_{i} – \sum_{k=1}^{j} r_{i,k} \tag{3}
$$
と書くことができます。ちなみに記号は何でも良いのですが、\(a_{i,j}\)は”asset”の頭文字、\(g_{i}\)は”gain”の頭文字、\(r_{i,j}\)は”reduction”の頭文字から取ってきています。
式(3)を図にすると、図2のようになります。\(i\)年に作られたモノの価値の総量\(g_{i} = a_{i,0}\)は、時間の経過とともに\(j\)年後に\(r_{i,j}\)だけ減少していきます。
償却率\(\alpha_{i}\)の導入
ここで、償却率\(\alpha_{i}\)を導入します。残存価値の減少量\(r_{i,j}\)は、前年に残っている価値\(a_{i,j-1}\)のうち一定の割合\(\alpha_{i}\)になると仮定します。すなわち、
$$
r_{i,j} = \alpha_{i} a_{i,j-1} \tag{4}
$$
とします(図2)。図2の例では、残存価値が毎年半分になっていくように\(r_{i,j}\)を設定しています。つまり\(r_{i,j} = 0.5 \times a_{i,j-1}\)です。このように残存価値のうちのある割合が減少するという定式化がわかりやすくて便利です。
ここで、償却率\(\alpha_{i}\)は\(i\)に依存するけれども\(j\)には依存しないことにしておきます。すなわち、モノが生産された年によって耐用年数は変わるけれども、ある年に生産されたモノの償却率はその後一定であるということです。
式(1)と(4)より
$$
\begin{align}
a_{i,j} &= a_{i,j-1} – r_{i,j} \\
&= a_{i, j-1} – \alpha_{i} a_{i, j-1} \\
&= a_{i, j-1}(1 – \alpha_{i})
\end{align}
$$
という漸化式を作ることができます。この漸化式を進めると
$$
\begin{align}
a_{i, j} &= a_{i, 0} (1-\alpha_{i})^{j} \\
&=g_{i} (1-\alpha_{i})^{j} \tag{5}
\end{align}
$$
となります。これで、\(g_{i}\)と\(\alpha_{i}\)が与えられるだけで、\(j\)年後の残存価値を計算することができます。
モノの価値の総量を実際に測定するのは困難
ここで、式(3)や(5)に登場する数値を実際に測定することは困難です。特に、市場に残るモノの価値の総量\(a_{i,j}\)や経年で減少する価値の総量\(r_{i,j}\)の実際の数字を測定することはできません。というのも、ここでいうモノとは、あらゆる商品やサービスを総称した概念だからです。日本で生み出されるすべての商品やサービスの価値をすべて足し合わせたものが\(a_{i,j}\)や\(g_{i}\)、\(r_{i,j}\)となります。個別の商品を想定していないので、消費や経年劣化による価値の減少\(r_{i,j}\)や、価値減少を加味したうえで市場に残るモノの価値\(a_{i,j}\)を具体的な数字として測定するのは難しいのです。
新たに生産されたモノの価値はGDPとして測定できる
ただし、式(3)や(5)に登場する数値のうち、新たに作られるモノの価値の総量\(g_{i}\)は国内総生産(GDP)として推定することができます。なぜなら、GDPは日本国内である年に新たに生み出された商品やサービスの価値の総量として推定されており、これは\(g_{i}\)と同じ概念だからです。逆に\(g_{i}\)は、企業活動の量(市場へのモノの供給量)を表すマクロ経済における重要な指標なので、GDPとして推定されていると考えることもできます。GDPが並々ならぬ努力によって推定されているのは、マクロ経済の状況を推し量るために重要な指標だからでしょう。
Result | 市場に残るモノの価値の総量の時間変化
ある年に生産されたモノの価値の時間変化が定式化できたので、次に、市場に残っているモノの価値の総量の時間変化を考えます。これまでの生産活動によって市場にどれだけのモノが蓄えられてきたのか、すわなち\(a_{i,j}\)の\(i\)についての積分を考えます。ここでは、式(5)の記号に着目し、
- モノの生産量\(g_{i}\)が一定かつ償却率\(\alpha_{i}\)が一定の場合
- モノの生産量\(g_{i}\)が\(i\)に伴って増加する場合
- 償却率\(\alpha_{i}\)が\(i\)に伴って減少する場合
の3通りについて、市場に残るモノの価値の時間変化を考えます。これらを考えることで、経済成長が続く場合に市場に蓄えられるモノの価値の総量がどのように推移するのか、技術革新や生産性向上によって市場に蓄えられるモノの価値の総量の推移にどのような影響があるのかを考察することができます。
市場に残るモノの価値の総量の定式化
市場の残るモノの価値の総量の時間変化を考える前提として、式(3)を使って、これまでに生産されたモノのうち、ある年に市場に残っているモノの価値の総量、すなわち市場に蓄えられてきたモノの価値の総量を定式化しておきます。式(3)の\(a_{i,j}\)は\(i\)年に生産されたモノの\(j\)年後の価値です。したがって、これまでに生産されてある年に市場に残っているモノの価値の総量は\(a_{i,j}\)を\(i\)について足し上げたものになります。ただし、\(j\)は各生産年\(i\)から市場に残っているモノの価値の総量を計算したい年までの経過年数です。したがって、\(n\)年に市場に残っているモノの価値の総量は
$$
\begin{align}
A_{n, N} &= a_{n,0} + a_{n-1, 1} + a_{n-2, 2} + \dots + a_{n-N, N} \\
&= \sum_{i=n-N}^{n} a_{i, n-i} \tag{6}
\end{align}
$$
と定式化することができます。ここで\(N\)は何年前の生産までを含めるかという年数を設定するための数字です。つまり、\(A_{n,N}\)は\(N\)年前から市場に蓄えられて\(n\)年時点で残存しているモノの価値の総量です。
以下では、図を使って具体的に3通りについての市場に残るモノの価値の時間変化を考えていきます。式(6)が理解の助けとなればよいですが、式(6)が理解できなくても以下の内容は理解できるのでご安心ください(笑)。
モノの生産量\(g_{i}\)と償却率\(\alpha_{i}\)が一定の場合 | 市場に残るモノの価値の総量は飽和
まずは毎年のモノの生産量\(g_{i}\)と残存価値の償却率\(\alpha_{i}\)が一定の場合を考えます。この場合には市場に残るモノの価値の総量はある時点で飽和してそれ以上増えなくなります。
図3は、モノの生産量\(g_{i}\)と残存価値の償却率\(\alpha_{i}\)が一定の場合の市場に残るモノの価値の総量の推移の例です。図3の例では、モノの生産量は\(g_{i} = g = 100\)で一定、償却率は\(\alpha_{i} = \alpha = 0.5\)で一定としています。
モノの生産量\(g_{i}\)が増加する場合 | 市場に残るモノの価値の総量は増え続ける
次に、モノの生産量\(g_{i}\)が年々増え続ける場合を考えます。例えば、経済成長してGDPが成長していくような状況が想定されます。ここでは償却率は一定と仮定します。この場合には市場に残るモノの価値は飽和することなく増え続けていきます。
図4は、モノの生産量\(g_{i}\)が年々増え続ける場合の市場に残るモノの価値の総量の推移の例です。図4の例では、モノの生産量は、初年\(g_{1} = 100\)で以降、毎年5%ずつ増える設定にしています。償却率は\(\alpha = 0.5\)で一定です。\(g_{i}\)はGDPと同義なので、GDP成長率5%の国では、市場に残るモノの価値の総量はこのように増えていくことになります。
図3の\(g_{i}\)が一定の場合には、市場に残るモノの価値の総量は200ぐらいで飽和しましたが、図4の場合には3年後に200を超え、10年後には300に達しています。つまり\(g_{i}\)が5%ずつ増える場合には、\(g_{i}\)一定の場合と比べて、市場に残るモノの価値の総量は10年で1.5倍程度多くなります。
償却率\(\alpha_{i}\)が減少する場合 | 市場に残るモノの価値の総量は増え続ける
次に、モノの残存価値の償却率\(\alpha_{i}\)が年々減っていく場合を考えます。生産技術が上がって、耐用年数が長くなっていく状況が想定されます。ここではモノの生産量\(g\)は一定と仮定します。この場合には、市場に残るモノの価値は飽和することなく増え続けていきます。
図5は、モノの残存価値の償却率\(\alpha_{i}\)が減っていく場合の市場に残るモノの価値の総量の推移の例です。図5の例では、償却率は初年の\(\alpha_{1}=0.5\)以降、毎年5%ずつ減少していきます。例えば、2年目と10年目を比較すると、生産量は一定なので\(g_{2} = g_{10}\)ですが、償却率が年々減少していく(\(\alpha_{i+1} < \alpha_{1}\))ので、1年目に生産されたモノの1年後の残存価値\(a_{1,1}\)よりも9年目に生産されたモノの1年後の残存価値\(a_{9,1}\)の方が大きくなります。したがって、年々、残存価値が増えていくため、市場に残るモノの価値の総量も増えていきます。
Discussion | 経済成長や技術革新が続く限りモノは増え続ける
マクロ経済における企業の役割がモノの生産である中で、経済成長、技術革新や企業の生産性の向上が続く限り、市場に残されるモノの価値の総量は増え続けていきます。Resultのセクションでは
- モノの生産量\(g_{i}\)の増加
- モノの償却率\(\alpha_{i}\)の減少(=耐用年数の向上)
によって、市場に残されるモノの価値の総量が際限なく増えていくことを確認しました。経済成長、技術革新や企業の生産性の向上はモノの生産量\(g_{i}\)の増加やモノの償却率\(\alpha_{i}\)の減少につながるため、市場に残されるモノの価値の総量を増やす方向に作用します。以下で詳しく見ていきましょう。
経済成長→モノの生産量\(g_{i}\)の増加
経済成長すなわちGDPの成長はモノの生産量\(g_{i}\)の増加に直結します。 したがって、経済成長が続く限りモノの生産量\(g_{i}\)は増加しつづけ、市場に残されるモノの価値の総量は増え続けていきます。もちろん、モノの償却率\(\alpha_{i}\)が増加(=耐用年数の減少=粗悪品の増加)が起これば、モノの生産量\(g_{i}\)の増加の効果が打ち消されます。しかし、経済成長に伴って粗悪品を作るようになっていくということは考えにくいので、経済成長が続く限り、市場に残されるモノの価値の総量は増え続けると考えて良いでしょう。
技術革新・生産性向上→モノの生産量\(g_{i}\)の増加・償却率\(\alpha_{i}\)の減少
技術革新は生産されるモノの価値\(g_{i}\)の増加や償却率\(\alpha_{i}\)の減少に繋がります。技術革新によって、同じ費用・同じ労働力・同じ労働時間を投入した場合でも
- 同じ労働力や資金からよりたくさんのモノを生産できるようになる: \(g_{i}\)が増加
- 生産された商品が高機能になる: \(g_{i}\)が増加
- ノウハウの蓄積によってより価値の高いサービスが提供できるようになる: \(g_{i}\)が増加
- 商品の寿命が伸びて経年劣化が低減される: \(\alpha_{i}\)が減少
といった効果があるため、\(g_{i}\)は増加傾向、\(\alpha_{i}\)は減少傾向となります。したがって、技術革新や企業の生産性の向上が続く限り、市場に残されるモノの価値の総量は増え続けると考えて良いでしょう。
提言 | 市場に残るモノの価値の総量\(A_{n, N}\)やモノの償却率\(\alpha_{i}\)を測定する指標が必要
最後にこれまでの議論から「市場に残るモノの価値の総量\(A_{n, N}\)やモノの償却率\(\alpha_{i}\)を実際の世の中で測定する指標が必要である」という提言をしておきましょう。ある年のモノの生産量\(g_{i}\)はGDPという指標で実際の世の中で測定されています。しかし、GDP(\(g_{i}\))だけでなく、経年の変化を測定するために\(\alpha_{i}\) and/or \(A_{n, N}\)も測定されるべきです。
市場に残るモノの価値の総量\(A_{n, N}\)は物価上昇や物価下落といった経済の状況に直接影響を与えます。原理的には、物価は市場に残るモノの価値の総量と市場に出回る通貨の総量で決まります。市場に出回る通貨の総量はマネタリーベースやマネーストックなどの指標で測定されています。もちろん物価が測定されているので、物価を通してモノの価値の総量\(A_{n, N}\)を推定することも可能ですが、モノの価値の総量\(A_{n, N}\)を直接測定し、マクロ経済全体の様子を掴むことが必要なはずです。
市場に残るモノの価値の総量\(A_{n, N}\)を直接測るのは難しくとも、ある年に生産されたモノの価値の総量の減少率である\(\alpha_{i}\)を測定することで、\(A_{n, N}\)を推定することも可能です。今は国内総生産GDPが測定されていますが、ある年の国内総生産のうち1年後にどのくらいの価値が残存するのかも測定される必要があります。\(g_{i}\)に加えて、\(\alpha_{i}\)が測定されれば、式(5)と(6)を通じて市場に残るモノの価値の総量\(A_{n, N}\)を計算することができます。いずれにせよ、モノの価値の総量\(A_{n, N}\)を測定する努力を行い、マクロ経済全体の様子を掴むことが重要であると考えます。
Conclusion | まとめ
今回はここまでです!
マクロ経済モデルの中での企業の役割がモノの生産であることを紹介しました!企業が生産活動をすることで、商品やサービスなどのモノが市場に供給され、国が豊かになります。
さらに、経済成長や技術革新、生産性の向上によって、市場に残されるモノの価値の総量が増え続ける傾向にあることも考察しました。この話が次回以降にお話する政府の役割(=通貨供給量の調整)や物価と関係してきます。次回は、マクロ経済モデルの中での政府の役割についてお話します!お楽しみに!
以上「天文学者のマクロ経済学#2|企業の役割はモノの生産(マクロ経済モデルの登場人物1)」でした!
最後までご覧いただきありがとうございました!
次回もお楽しみに!
Tips | 今回のPythonサンプルコード
今回の作図に使ったPythonのコードの実装例を掲載します(Jupyter Notebook)。参考にどうぞ!