Ciao!みなさんこんにちは!このブログでは主に
(1)pythonデータ解析,
(2)DTM音楽作成,
(3)お料理,
(4)博士転職
の4つのトピックについて発信していきます。
今回はpythonデータ解析編、知っていると便利な確率分布、JohnsonのSU分布についてお話します。
確率分布は乱数を作ったり、現実のデータをモデル化したりする際に、データサイエティストにとって不可欠ですよね!
でも、正規分布以外の確率分布を実際に扱ったことがない方も多いのではないでしょうか?
現実の世界には、
- 左右対称ではない
- 裾野が広がっている
といった分布を持つデータが存在します。
「正規分布を当てはめるのは明らかに良くないけど、どうしたらいいかわからない!」
今回はそんなあなたのお悩みを解決します!
この話題は導入編、基礎編、実践編の3回に分けて扱います。
今日は導入編!
まずはJohnsonのSU分布が必要になる現実のデータの例をご紹介します!
また、次回の基礎編では、JohnsonのSU分布の確率密度関数、そのパラメータを変化させると分布の形がどう変わるかなどの性質をご紹介します。
最後に実践編では、pythonを使って、JohnsonのSU分布を実際のデータに当てはめる例をご紹介します!
Abstract | 非対称性 and/or 裾野が広い ⇒ JohnsonのSU分布の出番!
現実世界のデータに正規分布が当てはまらないときには、JohnsonのSU分布を試してみてください。
現実世界のデータは、左右非対称な分布や裾野が広がっています。
よく知られている正規分布には、単純ゆえに解釈性が高いメリットがありますが、
(1) 非対称性を取り込めない
(2) 裾野の広がりを取り込めない
というメリットがあります。
非対称性のことを歪度、裾野の広がりのことを尖度といいます。
JonsonのSU分布は、正規分布に歪度と尖度を加えたものです。
なので、非対称性と裾野の広がりによって正規分布を当てはめることが難しい場合には、JonsonのSU分布を当てはめるとうまくいくことがあります。
JonsonのSU分布の詳しい性質は次回の基礎編でお送りします。
今回は導入編として、JonsonのSU分布が活躍する現実のデータの例をご紹介します!
Background | 正規分布が当てはまらない現実データの分布
同僚Tさんのお悩み | 経済指標の分布に正規分布が当てはまりません!
データサイエンティストとして働く著者Kaiko、同僚のTさんからこんな相談を受けました
Kaikoさん!助けてください!私がジョインしているプロジェクトで困ったことがありまして…お知恵を貸していただけないでしょうか?
お!Tさん、どうしました?
経済学者によるGDP成長率予測値の集計結果がありまして、
4パーセンタイル(以下%-tile): 7.9 %,
10 %-tile: 5.9 %,
50 %-tile: 2.6 %,
75 %-tile: 1.4 %,
90 %-tile: – 1.9 %,
96 %-tile: -4.3 %,
という6つの値だけがわかっているんです。
これに連続的な確率分布を当てはめたいのです。
そして、その確率分布の25 %-tile以下だけの範囲で、GDP成長率予測値の期待値を計算したいのです。
*\(x\)パーセンタイル値とは、その値より上(あるいは下)に、全体の\(x\) %が含まれるような値のことです。受験者100人のテストなら25位の人の点数が25 %-tileの値になります。
データが6点あるし、正規分布を当てはめるのはすぐできそうですね。
分布が歪んでいるのが問題なのかな?
はい、分布が左右対称でないので、以下のように正規分布が当てはまらないんです。10 %-tileと50 %-tile, 90 %-tileと50 %-tileの差が均等ではないんです。
さすがに無理やり正規分布を当てはめて25 %-tile以下の期待値を計算するには無理がある気がしまして…
でも正規分布以外に、解釈しやすくて使いやすい分布ってあまりないんですよね。。
集計結果の4, 10, 90, 96 %-tile点は正規分布よりも左にずれている。
つまり、分布の右側が狭く、左側が広い「左右非対称な分布」になっている(90 %-tileと50 %-tileの差と10 %-tileと50 %-tileの差も比べてほしい)。
なるほど…解釈性があって左右非対称性を入れられる分布ね。。
正規分布に尖度(尖り具合もしくは裾野の広がり具合)と歪度(左右非対称具合)を入れられれば良さそうですね!
ヒストグラムの尖度と歪度の計算の仕方は知っているのですが、それらをパラメータとして取り入れた分布があるんですか!?
天文学の研究で一度使ったことがあるのですが、なかなか便利な分布があるんです。
JohnsonのSU分布というものです!
天文学とSU分布 | 銀河の形の分布の場合
自然界のデータは正規分布になることが多いのですが、天文学の研究でJohnsonのSU分布を使った例を紹介します。
これは私が修士課程で楕円銀河という天体の形を研究していた頃のことです。
楕円銀河は、完全な楕円形からはディスク型あるいは箱型にズレていることが知られています。
このズレ具合を表した\(a_{4}\)パラメータという指標があり、\(a_{4}\)が0だと完全な楕円、負だと箱型、正だとディスク型に分類されます。
上段: 楕円銀河の等面輝度線(明るさの等高線; シアンの実線)を完全な楕円(赤点線)と比較した例。左の銀河は四角く(箱型)、右の銀河はひし形(ディスク型)にずれている。
下段: \(a_{4}\)パラメータの計算方法。詳細には触れない。
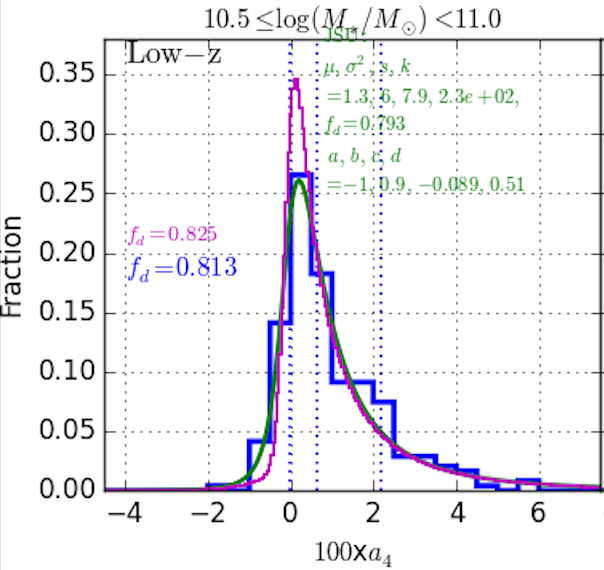
楕円銀河の\(a_{4}\)パラメータの分布を観測してみると、2 %ぐらいを中心に大きく正の方向に広がった分布になっています(下図、青いヒストグラム)。質量にもよりますが、ディスク型楕円銀河が大体8割くらいです。
当時、この\(a_{4}\)の分布を再現する関数を作ってシミュレーションをする必要がありました。
これだけ左右非対称だと正規分布を使うことはできません。
そこで行き着いたのがJohnsonのSU分布(下図、緑の曲線)だったというわけです。
Conclusion | 導入編のまとめ
JohsonのSU分布の第1回導入編、最後まで読んでいただきありがとうございます!
「確率分布といえば正規分布」と考えがちですが、現実の世界のデータには
- 無視できないレベルの非対称性がある
- 無視できないレベルの裾野の広がり具合がある
など、正規分布を当てはめることができないケースが発生します。
このような場合にはJohnsonのSU分布の出番です!
今回は経済のデータ、天文学のデータの例を紹介しました。
みなさんの周りでもJohnsonのSU分布が活躍するケースがきっとあるはずです!
以上、「統計学レシピ|正規分布を超えたいあなたに捧げるJohnsonのSU分布(導入編)」でした!
次回の基礎編ではJohnsonのSU分布の関数形や性質などをご紹介します!
ちょっとマニアックな内容ですがお楽しみに!Ciao!
References | 参考
Wikipedia (英語版のみ): https://en.wikipedia.org/wiki/Johnson’s_SU-distribution
よくまとまったExcellアドインのサイト: http://www.ntrand.com/jp/johnson-su-distribution/
Bender & Moellenhoff, 1987: https://ui.adsabs.harvard.edu/abs/1987A%26A…177…71B/abstract